Функция корреляции нерперывного процесса
Рисунок 7.14. Сущность вычисления функции корреляции
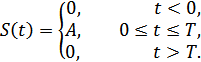
Считаем, что процесс эргодический: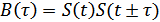 
.
Напишем функцию корреляции отдельно для (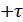 
) и ( 
):
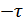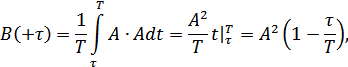
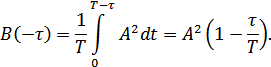
Окончательно:
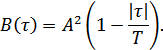
Функция корреляции четная.
Рисунок 7.15. Функция корреляции непериодического сигнала
Функция корреляции периодического сигнала
ДАМ:
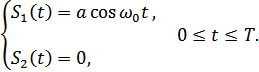
Рисунок 7.16. Временное представление периодического сигнала
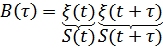
– функция корреляции в общем виде.
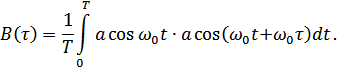
Учитывая элементарные тригонометрические преобразования, в результате получим:
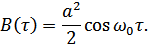
Функция корреляции будет иметь вид:
Рисунок 7.17. Функция корреляции периодического сигнала
Вывод:
У периодического сигнала функция корреляции является периодической фукцией 
той же частоты 
.
7.8. Применение корреляционных методов обработки сигналов в технике связи
Устройства позволяющие определить функцию корреляции сигнала называются корреляционными. Они широко используются для обработки сигналов на приеме с целью принятия решения о переданном сигнале.
Два основных способа приема:
1) взаимнокорреляционный прием;
2) автокорреляционный прием.
Все взаимнокорреляционные способы приема основываются на вычислении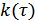 
.
Рисунок 7.18. Структурная схема взаимнокорреляционного приемника
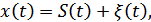
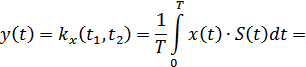
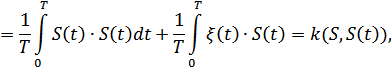
где 
– переданный сигнал,
– принятый сигнал,
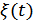– помеха.
Автокорреляционный приемник
Рисунок 7.19. Структурная схема автокорреляционного приемника
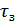– задержка на один элемент сигнала.
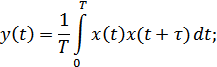
0 0
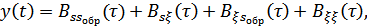
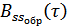– функция автокорреляции сигнала,
, 
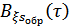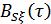– функции взаимной корреляции,
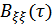– функция автокорреляции помехи.
Рисунок 7.20. Сущность выделения слабого сигнала на фоне помех
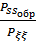растет, если увеличивается.
Чем больше , тем лучше (больше отношение мощности сигнала к помехе).
Данный способ приема называется выделением сигнала на фоне помех.
Часть II. Теория передачи сигналов
8. Случайные сигналы
8.1. Энергетический спектр случайных сигналов
При наблюдении за течением случайного процесса (СП) мы можем определить лишь текущий спектр данной реализации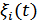 
, т.е.
Рисунок 8.1. Реализация случайного процесса
