Математическое ожидание случайного процесса
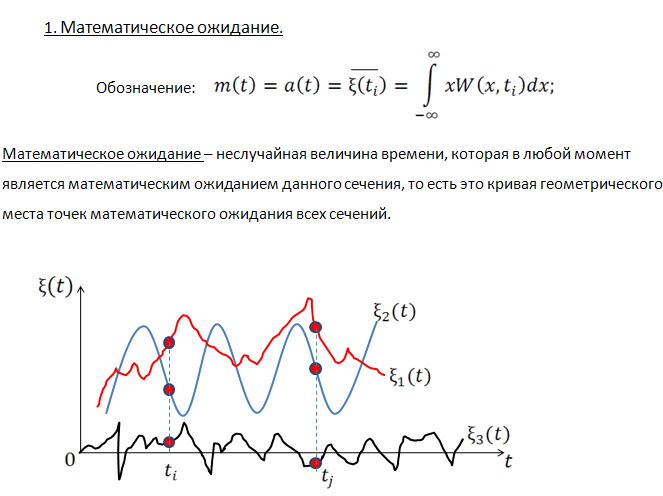
Рисунок 7.2. Три реализации случайного процесса с различным математическим ожиданием
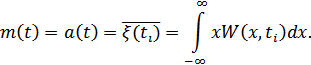
Математическое ожидание случайного процеса представляет собой неслучайную функцию времени, которая в любой момент времени является математическим ожиданием данного сечения, т.е. это есть кривая геометрического места точек математических ожиданий всех сечений. Геометрически – некоторая средняя кривая не выходящая за границы реаализации, т.е. среднее значение переменной.
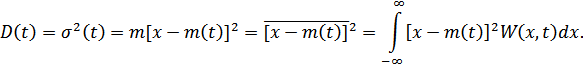
Дисперсия есть математическое ожидание квадрата отклонения значений случайного процесса; она характеризует степень разброса значений случайного процесса относительно математического ожидания.
Рисунок 7.3. Две реализации случайного процесса (а, б) при одинаковом математическом ожидании и различных дисперсиях
Корреляционные функции – xарактеризуют статистическую связь между сечениями случайных процессов. Может быть четыре разновидности корреляционных функций:
1. Ковариационная фунция.
Рисунок 7.4. Сущность определения корреляционных функций
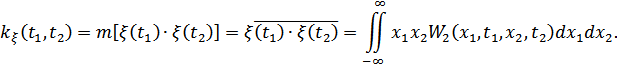
Ковариационная функция – математическое ожидание произведения значений случайного процесса в 2 различных моментах времени.
2. Корреляционная функция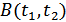 
определяется для центрированного случайного процесса.
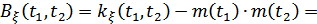
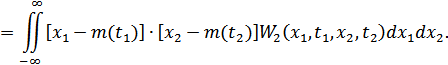
Рисунок 7.5. Физический смысл некоторых характеристик случайного процесса
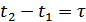– расстояние между сечениями.
3. Нормированная корреляционная функция.
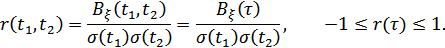
С увеличением 
функции 
, 
, 
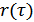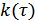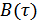будут уменьшаться.
4. Взаимная корреляционная функция характеризует связь между сечениями различных случайных процессов.
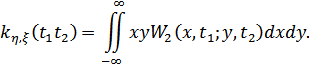
Замечание: если два процесса независимы, то их функция взаимной корреляции равна 0.
7.3. Стационарные случайные процессы
Случайные процессы
Стационарные Нестационарные
(установившиеся) (неустановившиеся)
Стационарные в Стационарные в
Узком смысле широком смысле
Стационарность в узком смысле – случайные процессы у которых 
– мерная плотность вероятностей не зависит от сдвига всех сечений влево или вправо на одну и ту же величину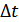 
.
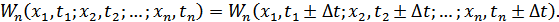
Свойства стационарных (в узком смысле) случайных процессов:
1. 
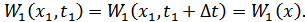
2. 
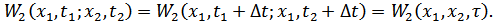
3. 
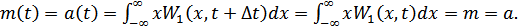
4. 
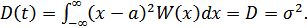
5. 
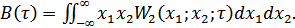
Выводы:
1. Одномерная функция плотности вероятностей, математическое ожидание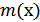 
и дисперсия 
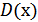не зависят от времени.
2. Двумерная функция плотности вероятностей и функция корреляции не зависят от временя, а зависят от интервала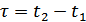 
.
3. Процесс (случайный) называется стационарнымв широком смысле если его характеристики не зависят от времени (т.е. выполняется условие 2, 3 и 4).
4. Случайный стационарный процесс в узком смысле всегда стационарен и в широком. Случайный стационарный процесс в широком смысле не всегда стационарен в узком.
Свойства функции корреляции стационарных процессов:
1. Функция корреляции действительная и четная, т.к. это функция времени: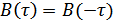 
.
2. 
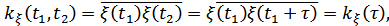если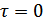 
,
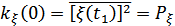– полная мощность процесса (рис. 7.5).
3. 
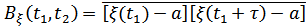при
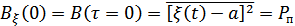– мощность переменной составляющией (рис. 7.5).
4. 
.
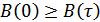Рисунок 7.6. Физический смысл энергетических характеристик функции корреляции
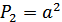– мощность постоянной составляющей,
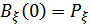– полная мощность процесса,
– мощность переменной составляющей.
7.3. Интервал корреляции