Детерминированные процессы – это процессы, течение которых во времени известно заранее и обсолютно точно.
Например, гармонический сигнал
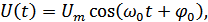
где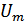 
, 
, 
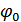– заданы.
Это простейшая модель информационного сигнала, но она оказывается неточной для современных систем связи, дает большие погрешности в расчетах. Поэтому вводится новая модель, более сложная – случайные процессы (СП). Случайные процессы таковы, что их течение во времени заранее точно предсказать невозможно.
– сложная случайная функция времени; ее графическое представление:
Рисунок 7.1. Временное представление трех реализаций случайного процесса
, 
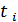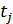– сечения случайного процесса,
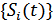– совокупность случайных функций (случайных процессов).
Любой сложный случайный сигнал можно представить совокупностью всех возможных его реализаций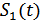 
, 
, 
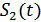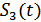и т.д.
Реализация случайного процесса – конкретный вид, который принимает процесс в данном испытании.
Сечение – конкретное значение реализации случайного процесса в некоторый произвольный, но фиксированный момент времени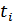 
, т.е. 
.
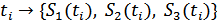Достоинства графического представления: наглядность, полное представление.
Недостатки: громозкость, трудность в вычислении.
Необходимо найти математические методы описывающие СП и его характеристики. Для этого используется теория вероятностей. Значение сигнала в сечении является случайной величиной. Поэтому для описания случайных сигналов вводят понятие функции плотности вероятностей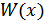 
(ФПВ) и функцию распределения вероятностей 
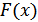(ФРВ).
Одномерная функция распределения вероятностей характеризует процесс только в одном сечении – .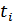
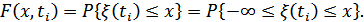
n -мерная функция распределения вероятностей характеризует случайный процесс одновременно в n сечениях:
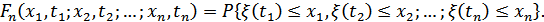
Функция плотности вероятностей случайного процесса:
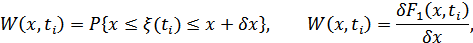
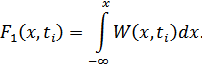
Для n-мерной функции плотности вероятностей:
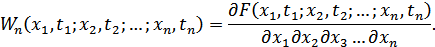
Значения Wn используются при оценке помехоустойчивости приема сигналов методом многократных отсчетов.
Двумерная функция распределения вероятностей широко используется в теории связи.
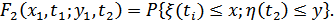
Т.е. F2 учитывает два процесса: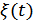 
и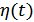 
.
Свойства функции распределения вероятностей и функции плотности вероятностей:
1. 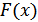– функция неубывающая.
Если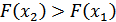 
, то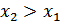 
.
2. 
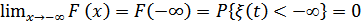– невозможное событие.
3. 
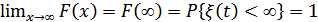– достоверное событие.
4. 
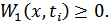
5. 
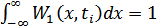– условие нормировки.
7.2. Числовые характеристики случайных процессов
Полным описанием любого случайного процесса является n-мерная функция распределения вероятностей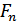 
или n-мерная функция плотности вероятностей 
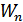. Однако, не всегда есть необходимость иметь полное, но очень сложное описание случайного процесса. На практике достаточно знать усредненные (числовые) характеристики:
1) математическое ожидание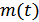 
;
2) дисперсию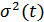 
;
3) функцию корреляции.