Количество уровней квантования
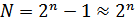, если 
.
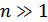Интервал квантования
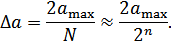
Мощность шумов квантования (при условии, что импульсы треугольной формы)
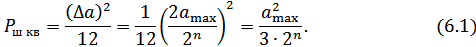
Нас интересует отношение мощности сигнала к мощности шума квантования. При этом рассматривается наихудший случай, когда мгновенная амплитуда,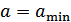 
. В этом случае минимальная средняя мощность сигнала будет зависеть от 
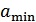и от пик-фактора сигнала 
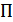(отношение максимального значения к среднеквадратическому)
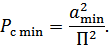
Если задать отношение мощности сигнала при минимальной его амплитуде к мощности шума квантования:
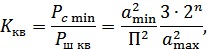
можно определить число разрядов 
:
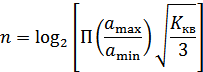
а значит, и число уровней квантования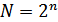 
.
6.5. Использование компандирования в ИКМ
Из выражения (6.1) следует, что мощность шума квантования пропорциональна квадрату ширины интервала квантования (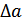 
) и не зависит от величины сигнала. В связи с этим при уменьшении уровня сигнала снижается отношение сигнал/шум квантования. Чтобы получить приблизительно постоянное, не зависящее от уровня сигнала отношение сигнал/шум квантования, следовало бы использовать переменную ширину шага квантования: малую для малых сигналов, большую для больших сигналов. Поэтому вводимые в кодер дискреты (отсчеты) пропускают через, так называемый, мгновенный компрессор (постоянная времени которого практически равна нулю) с соответствующей характеристикой. Преобразованный соответствующим образом в компрессоре дискрет (отсчет) затем кодируется как при использовании равномерных шагов квантования. Такая схема эквивалентна схеме с делением всего диапазона на интервалы переменной ширины.
Рисунок 6.14. Струтктурная схема передающей части системы с ИКМ
На приеме кодовых комбинаций подвергается декодированию, а затем полученные дискреты вводятся в экспандер, характеристика которого обратна характеристике компрессора.
Рисунок 6.15. Струтктурная схема приемной части системы с ИКМ
Выигрыш от применения компандера показан на рис. 6.16. На этом рисунке по оси абсцисс представлен уровень сигнала, а по оси ординат указано отношение уровней сигнала и шума квантования.
Рисунок 6.16. Выигрыш в использовании компандера
6.6. Системы передачи с дельта-модуляцией
Принцип работы системы связи с дельта-модуляцией состоит в том, что передается информация не о мгновенной величине дискрета, а только сообщение о том, больше или меньше данный дискрет по отношению к предыдущему переданному значению сигнала. Поскольку существует одна из двух указанных возможностей (случай идеального равенства как маловероятный не принимается во внимание), то информация об этом может быть передана с помощью одного элемента: единицы (импульса), если данный дискрет больше предсшествующего, или нуля (пробела), если он меньше. Очевидно, что указанная информация должна передаваться значительно чаще по сравнению с дискретами в системе передачи с ИКМ (рис. 6.17).
Рисунок 6.17. Сущность передачи сигналов с использованием дельта-модуляции
7. Случайные процессы
7.1. Вероятносные характеристики случайных сигналов (процессов); числовые характеристики и физическая интерпретация
Как уже говорилось, процессы, рассматриваемые в теории связи, могут быть детерминированными или случайными.