Временное, спектральное и векторное представление сигнала угловой модуляции
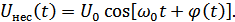
ЧМ – изменение частоты несущей.

ФМ – изменение фазы несущей по закону низкочастотного сигнала.
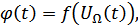
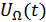 – модулирующее колебание.
– модулирующее колебание.
5.1. Фазовая модуляция
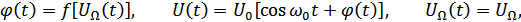
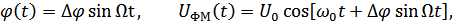
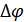 – девиация фазы – максимальное отклонение фазы в процессе модуляции от среднего значения.
– девиация фазы – максимальное отклонение фазы в процессе модуляции от среднего значения.
Аналитическое представление:
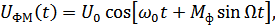
где 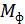 – индекс фазовой модуляции,
– индекс фазовой модуляции, 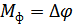 .
.
Векторное представление:
Рисунок 5.1. Векторная диаграмма УМ-сигнала
5.2. Частотная модуляция
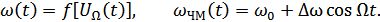
Частоту в таком виде изменить нельзя, поэтому вводится понятие мгновенной фазы 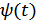 .
.
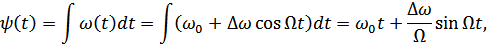
∆ ω – девиация частоты, т.е. максимальное отклонение частоты от среднего значения.
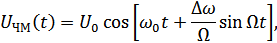
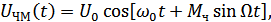
где 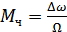 – индекс частотной модуляции.
– индекс частотной модуляции.
Если 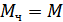 и
и 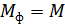 , то
, то
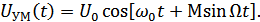
5.3. Сравнение ЧМ и ФМ
1. При модуляции чистым тоном или одной частотой 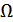 временные функции одинаковы и по существу не отличаются одна от другой.
временные функции одинаковы и по существу не отличаются одна от другой.
2. Отличия:
Т.к. 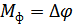 , а
, а 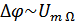 , то
, то 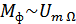 .
.
Т.к. 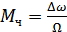 , а
, а 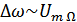 , то
, то 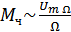 .
.
Видно, что индекс 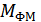 не зависит от частоты модулирующего сигнала
не зависит от частоты модулирующего сигнала 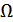 , а
, а 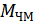 обратнопропорционален частоте модулирующего сигнала
обратнопропорционален частоте модулирующего сигнала 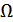 .
.
3. Поскольку 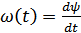 – скорость изменения фазы и
– скорость изменения фазы и 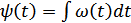 – пройденный путь, то один вид модуляции можно получить из другого.
– пройденный путь, то один вид модуляции можно получить из другого.
4. Т.к. 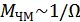 , то спектральные диаграммы ЧМ от ФМ будут отличаться изменением эффективной ширины спектра сигналов в зависимости от модулирующей частоты.
, то спектральные диаграммы ЧМ от ФМ будут отличаться изменением эффективной ширины спектра сигналов в зависимости от модулирующей частоты.
Таблица 2 – Спектры ЧМ и ФМ при различных модулирующих частотах.
Для ЧМ при увеличении частоты расстояние между спектральными составляющими увеличивается, но эффективная ширина спектра не меняется, для ФМ – расстояние между спектральными составляющими увеличивается и одновременно увеличивается эффективная ширина спектра (спектральные линии «расползаются»).
5.4. Модуляция сигналом произвольной формы
ЧМ и ФМ резко отличаются между собой при модуляции сигналом сложной (не 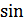 -ой) формы.
-ой) формы.
Таблица 3 – Модуляция ЧМ и ФМ сигналом сложной формы.
Примечание: особенностью угловой модуляции является то, что при изменении частоты будет изменяться и фаза и наоборот изменение фазы ведет к изменению частоты.
5.5. Спектры при угловой модуляции
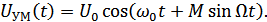
Различают два случая УМ:
1) 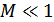 – узкополосная модуляция (УПУМ);
– узкополосная модуляция (УПУМ);
2) 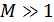 – широкополосная модуляция (ШПУМ).
– широкополосная модуляция (ШПУМ).
Рассмотрим 1-й случай:
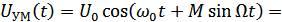
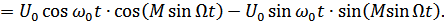
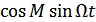 (при М <<1) ≈ 1,
(при М <<1) ≈ 1,
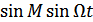 (при М >>1) ≈
(при М >>1) ≈ 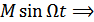
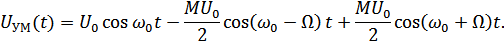
Полученное выражение напоминает спектр АМ сигнала, но отличается тем, что нижняя составляющая – отрицательна, т.е. повернута на 180°.
Таблица 4 – Спектры АМ и УМ.
Приведенное выражение приближенное, а в более точном появляются составляющие 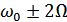 ,
, 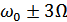 и т.д., но они очень малы.
и т.д., но они очень малы.
Выводы:
1. Отличие УПЧМ от АМ в том, что модулирующий вектор перпендикулярен вектору несущей (всегда).
2. При УП угловой модуляции результирующий вектор «качается» относительно 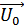 в ебе стороны на величину девиации
в ебе стороны на величину девиации 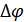 .
.
3. Видно, что при УП угловой модуляции появляется и паразитная АМ (т.к. 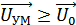 ).
).
Рассмотрим 2-ой случай:
Для cos и sin сложного аргумента используется разложение в ряд Бесселя.
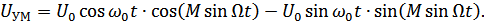
Разложим функции 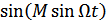 и
и 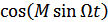 в ряд Бесселя:
в ряд Бесселя:
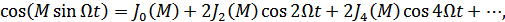
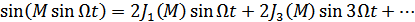
Рисунок 5.2. Вид функций Бесселя
Учитывая, что
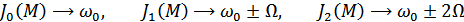
и т.д., получим:
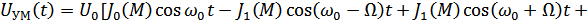
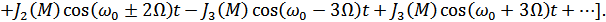
Рисунок 5.3. Спектры широкополосной угловой модуляции при различных индексах M
Выводы:
1. Спектр ШП угловой модуляции бесконечно широкий.
2. Колебания частоты  несет в себе информацию об
несет в себе информацию об 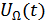 наравне с другими спектральными составляющими; при некотором
наравне с другими спектральными составляющими; при некотором 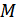
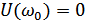 .
.
3. Практически ширина спектра определяется величиной М. Обычно спектральными состовляющими с частотой 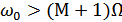 – пренебрегаем ввиду их малости:
– пренебрегаем ввиду их малости: 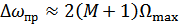 , а при
, а при 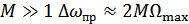 .
.
Примечание:
Для ЧМ 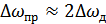 , где
, где 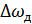 – девиация частоты. Т.к.
– девиация частоты. Т.к. 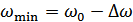 ,
, 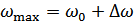 , то
, то 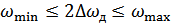 .
.
5.6. Сходства и различия ЧМ и ФМ
Вспомним, что:
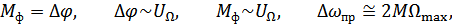
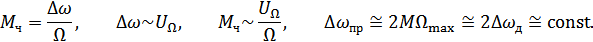
Отсюда можно сделать следующие выводы:
1. В обоих случаях 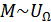 .
.
2. Ширина спектра при ЧМ не зависит от частоты сигнала и равна удвоенной девиации частоты.
3. При ФМ ширина спектра пропорциональна частоте модулирующего сигнала.
4. При ФМ колличество спектральных линий не меняется и равно 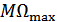 (штук).
(штук).
5. При ЧМ колличество спектральных линий изменяется, но остается неизменной эффективная (практическая) ширина спектра.
5.7. Методы получения сигналов угловой модуляции
Различают два основных метода:
1) прямой;
2) косвенный.
Под прямым методом понимают непосредственное воздействие на частоту или фазу задающего генератора.








