4.6. Определение глубины модуляции по спектральной диаграмме (графический метод)
, 
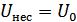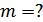
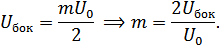
Векторное представление:
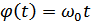– фаза колебания (пройденный путь),
– угловая скорость частоты.
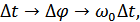
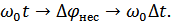
Рисунок 4.17. Векторная диаграмма АМ-колебания
Принято при изображении модулированного колебания вектор несущей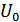 
считать неподвижным, а векторы боковых выражаются относительно концов несущей.
Рисунок 4.18. Векторное представление АМ-колебания в различные моменты времени (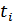 
, 
, 
)
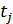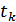Вывод:
Аналитическое, спектральное и векторное представление АМ сигнала равноценны и его полностью определяют.
4.7. Спектр АМ сигнала при модуляции сообщением сложной формы
Рассмотрим два случая:
1) cложное периодическое колебание;
2) cложное непериодическое колебание.
Колебание периодическое:
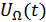– периодическое колебание,
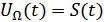– модулирующее колебание.
Данное колебание (функцию) можно разложить в ряд Фурье:
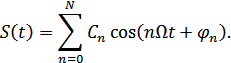
Количество гармоник по теореме Котельникова:
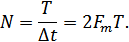
Основная частота (первая гармоника):
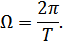
АМ колебание с учетом 
:
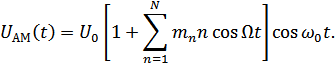
Порциональные коэффициенты модуляции:
Рисунок 4.19. а) временная характеристика модулирующего периодического
колебания;
б) спектр модулирующего периодического колебания;
в) спектр амплитудно-модулированного колебания
Сигнал непериодический:
Рисунок 4.20. а) временная характеристика непериодического колебания;
б) спектральная характеристика непериодического колебания;
в) спектральная характеристика непериодического амплитуд-но-модулированного колебания
Выводы:
1. Спектр АМ колебания получается из спектра НЧ путем переноса модулирующего сигнала по оси частот вправо на величину – ВБПЧ.
2. НБПЧ достраивается как зеркальное отображение ВБПЧ относительно , при этом амблитуды боковых уменьшаются в два раза по отношению к модулирующему сигналу.
4.8. Амплитудная модуляция с подавленной несущей (балансная модуляция)
Из смысла модуляции информацию передают НЧ состовляющие содержащиеся только в спектре боковых состовляющих т.е. в которых есть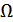 
.
Полезными являются только боковые частоты; – не содержит полезной информации, и ее целесообразно подавить. Такой вид модуляции называют балансной модуляцией (БМ).
Рисунок 4.21. а) спектр АМ-колебания при модуляции чистым тоном;
б) спектр АМ-колебания с подавленной несущей
Это дает существенный энергетический выигрыш. Оценим этот выигрыш.
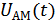определяет мощность:
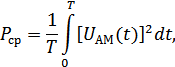
где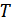 
– период наблюдения.
Составляющие спектра АМ-колебания:
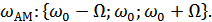
Из равенства Парсеваля для периодического сигнала:
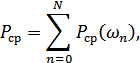
где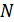 
– максимальный номер гармоники.
Средняя мощность на сопротивлении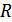 
:
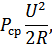
тогда
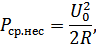
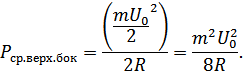
Суммарная мощность АМ:
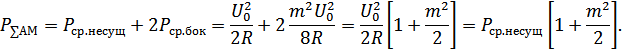
Рисунок 4.22. Спектр АМ сигнала с подавленной несущей
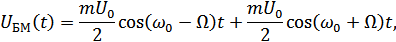
НБЧ ВБЧ
или во временной области:
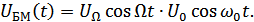
Модулированное БМ колебание получается перемножением НЧ сигнала и ВЧ сигнала.
Рисунок 4.23. Временная характеристика БМ-сигнала при модуляции чистым
тоном
Огибающая сигнала БМ не повторяет форму модулирующего сигнала.
Замечание: при детектировании БМ сигнала на приеме необходимо восстановить для нормальной работы детектора. БМ в технике связи применение не нашла.
Выводы:
1. Мощность боковых равна половине мощности несущей (при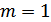 
).
2. Подавление несущей дает большой энергетический выигрыш.
3. Сэкономленную мощность можно направить на увеличение мощности боковых полос, что дает увеличение качества связи.
4.9. Однополосная АМ модуляция
Из спектра АМ колебания видно, что НБПЧ содержит ту же информацию, что и ВБПЧ, т.е. дублирует ее. Следовательно можно оставить одну из них. За счет этого можно уменьшить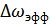 
в 2 раза.
Рисунок 4.24. а) спектр АМ модуляции;
б) спектр АМ с подавленной одной боковой (ОБП);
в) спектр ОБП с подавленной несущей
Полность подавлять несущую нельзя, т.к. возникнут трудности при детектировании.
4.10. Получение АМ колебаний
Модулятор – устройство, обеспечивающее получение модулированных колебаний (сигналов). В результате модуляции появляются новые частоты, которых не было в передаваемом сообщении, поэтому в модуляторе должны использоваться нелинейные или параметрические элементы. При воздействии сигнала на нелинейный элемент создается множество новых частот, как нужных, так и ненужных. Нужные частоты выделяются с помощью полосовых фильтров.
Функциональная схема
Рисунок 4.25. Сущность получения АМ-колебания
Рисунок 4.26. Принципиальная схема модулятора на диоде
Источник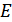 
задает рабочую точку.
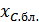– емкостное сопротивление.
,
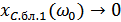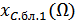→ большое,
,
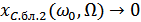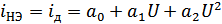– вольтамперная характеристика диода,
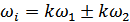, где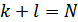 
,
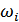– комбинационные частоты.
Рисунок 4.27. Сущность получения АМ-колебания
Спектр сигнала на выходе модулятора определяется следующим образом:
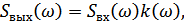
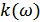– АЧХ L-фильтра.
Рисунок 4.28. Принципиальная схема модулятора на транзисторе
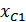– емкостное сопротивление, для низких частот большое, для высоких частот маленькое.
Вид модуляции и вид схемы определяется тем электродом усилительного элемента, на который подается модулирующее колебание.
4.11. Выбор режима работы модулятора для обеспечения неискаженной модуляции
Для правильного выбора режима работы модулятора используется статическая модуляционная характеристика (СМХ). Под неискаженной АМ понимается такая, при которой форма огибающей модулированного сигнала не отличается от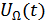 
.
СМХ – это зависимость амплитуды первой гармоники выходного тока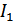 
модулятора (нелинейного элемента) от напряжения смещения 
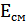при амплитуде ВЧ несущей 
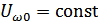и амплитуде НЧ модулирующего сигнала 
.
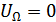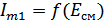при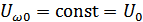 
, 
.
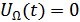Разновидности СМХ
СМХ может быть снята двумя способами:
1. 
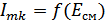– амплитуда тока в контуре,
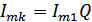– ток первой гармоники в контуре,
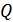– добротность контура.
2. 
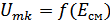– амплитуда напряжения в контуре, т.к. 
, 
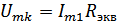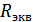– эквивалентное сопротивление на контуре.
Практически используется .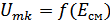
Рисунок 4.29. Схема снятия СМХ
Рассмотрим СМХ на примере полевого транзистора:
Рисунок 4.30. Зависимость тока стока от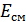 
Рисунок 4.31. Пример получения неискаженного АМ-колебания
Рабочая точка на СМХ выбирается следующим образом:
1. Определяем линейный участок и его границы.
2. На середине линейного участка выбираем рабочую точку (Р.Т.) и находим необходимое .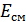
3. Определяем допустимая максимальная амплитуда модулирующего колебания в пределах линейного участка.
Замечание: выход 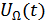за границы линейного участка приводит к линейным искажениям (сверху или снизу).
.
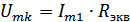Огибающая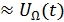 
.
Два типа искажения огибающей при неправильном выборе рабочей точки:
1) ограничение огибающей сверху (по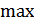 
) – Р.Т. смещена вправо;
2) искажение огибающей снизу (по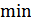 
– отсечка) – Р.Т. смещена влево.
Рисунок 4.32. а) Р.Т. смещена вправо (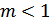 
);
б) Р.Т. смещена влево (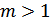 
)
4.12. Балансный модулятор
Для получения балансной модуляции (без несущей) должна быть использована только двухтактная схема.
Рисунок 4.33. Схема балансного модулятора на диодах
В этой схеме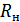 
состоит из 
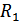и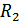 
.
где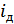 
– ВАХ,
Подставим (4.2) и (4.3) в (4.11), получим:
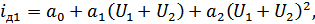
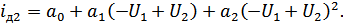
Из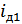 
вычтем 
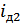и получим ток нагрузки 
:
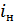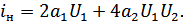
Вывод:
В двухтактной схеме ток нагрузки пропорционален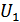 
и 
.
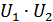Рассмотрим 2 варианта включения двухтактной схемы – в зависимости от того, чем являются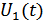 
и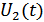 
(ВЧ или НЧ колебания).
1-ый случай:
| 
|
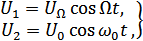
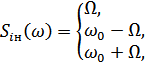
где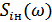 
– спектр тока, протекающего через нагрузку.
Рисунок 4.34. а) спектр тока на входе;
б) спектр тока, протекающего в нагрузке;
в) спектр тока, создающего напряжение на колебательном контуре
2-ой случай:
| 
|
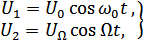
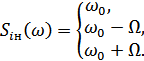
Рисунок 4.35. а) спектр тока на входе;
б) спектр тока на выходе (на нагрузке)
Контур на выходе не нужен, получаем классическую АМ.
4.13. Кольцевой модулятор (двойной балансный)
Рисунок 4.36. Функциональная схема кольцевого модулятора
Рисунок 4.37. Эквивалентная схема для тока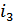 
Найдем ток нагрузки 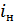, решив систему:
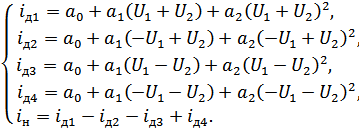
Получим:
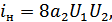
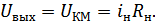
Выводы:
1. В спектре тока будут только комбинационные частоты.
2. Не нужен колебательный контур.
3. Данная схема инвариантна по отношению к 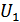и 
.
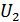Применения кольцевого модулятора:
1. Для получения балансной модуляции (БМ).
2. Для получения БМ с одной боковой полосой (ОБМ).
Рисунок 4.38. Структурная схема получения ОБП
3. Для преобразования частот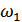 
и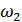 
в суммарную ( 
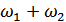) или разностную ( 
).
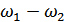4. Для измерения разности фаз сигналов одной частоты.
Пусть:
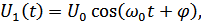
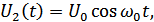
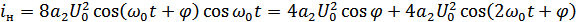
НЧ ВЧ
Элементарный ФНЧ:
Рисунок 4.39. Реализация измерения разности фаз сигналов 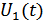и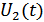
С помощью ФНЧ избавляемся от ВЧ.
5. В качестве синхронного детектора – фазовый детектор.
4.14. Амплитудные модуляторы на интегральных микросхемах
Ранее были рассмотрены модуляторы (балансный и кольцевой), токи в нагрузке которых соответственно:
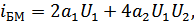
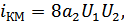
т.е. основной операцией получения АМ является операция перемножения, поэтому основным элементом интегральной микросхемы (ИМС) является перемножитель:
Рисунок 4.40. Эквивалентная схема перемножителя
Он должен осущесвлять перемножение двух аналоговых величин (низкочастотного и высокочастотного). Таковыми ИМС являются в частности: КР140МА1; К525ПС1; К525ПС2; К525ПС3.
В зависимости от структурной схемы и электрических параметров (характеристик) аналоговые перемножители делятся:
Рисунок 4.41. Классификация аналоговых перемножителей
Аналоговый перемножитель предназначен для реализации передаточной функции:
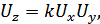
где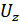 
– выходное напряжение,
, 
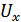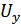– входные сигналы,
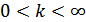– коэффициент пропорциональности.
Важнейшие параметры для АП:
- диапазон входного и выходного напряжения;
- диапазон частот поступающих сигналов;
- нелинейность перемножения,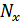 
, 
, %.
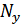Мы не будем детально рассматривать возможные схемы АМ на ИМС, а рассмотрим только принцмип их реализации на ИМС (рис. 4.42).
Рисунок 4.42. Условное графическое обозначение ИМС для АМ
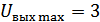B (по постоянному току),
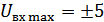B – диапазон линейных входных напряжений,
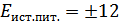В,
435МА1 – диодный мост (интегральная схема кольцевого модулятора).
4.15. Детектирование АМ колебаний (демодуляция)
Детектирование – процесс выделения НЧ переданного сообщения из принятого ВЧ модулированного сигнала. Это операция обратная модуляции.
Рисунок 4.43. Сущность детектирования
Временная характеристика:
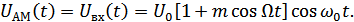
Спектр АМ колебания:
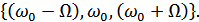
На рис. 4.44 представлены временные и спектральные характеристики токов детектора в различных точках схемы.
Рисунок 4.44. Временные и спектральные характеристики токов детектора:
а) на входе детектора;
б) протекающеих через нелинейный элемент;
в) на выходе детектора
Рисунок 4.44\5. Простейшая схема детектора
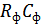→ ФНЧ – для выделения 
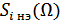полезной НЧ состовляющей и подавления ВЧ составляющих. Следовательно, должны выполняться соотношения:
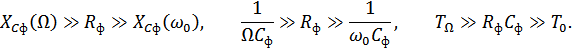
Работа детектора определяется характеристикой детектирования.