Если , то это линейная электрическая (радиотехническая) цепь (ЛЭЦ). Она состоит из линейных элементов , , .
Рисунок 4.1. Линейные элементы (ЛЭ)
Для линейной цепи справедлив принцип суперпозиции: реакция на суммарное воздействие равна сумме реакций на каждое из воздействий в отдельности.
Например:
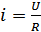 – характеристика ЛЭЦ.
– характеристика ЛЭЦ.
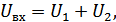
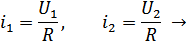
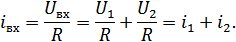
В линейной цепи невозможно появление новых частот, не содержащихся во входном воздействии (сигнале).
1. Если
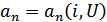 ,
,
то цепь называется нелинейной (НЭЦ) и состоит из нелинейных 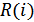 ,
, 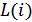 ,
, 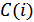 .
.
Рисунок 4.2. Нелинейные элементы (НЭ)
Для НЭЦ не справедлив принцип суперпозиции. Пусть НЭЦ описывается уравнением:
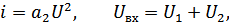

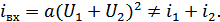
В НЭЦ возникают новые частоты, не содержащиеся во входном воздействии.
2. Если
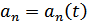 ,
,
то цепь называется параметрической (ПЭЦ) и состоит из элементов, зависящих от времени:
Рисунок 4.3. Параметрические элементы (ПЭ)
Для ПЭЦ:
а) справедлив принцип суперпозиции;
б) возможно появление новых частот.
ПЭЦ конструируется на основе нелинейных элементов, на которые мы подаем напряжение независящее от времени.
Рисунок 4.4. Пример использования параметрического элемента
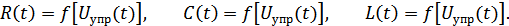
Принципы преобразования спектров
Рисунок 4.5. Использование ПЭ (НЭ)
Таблица 1 – Характеристики сигналов
| На входе НЭ (ПЭ) | На выходе НЭ (ПЭ) |
Спектр воздействия: 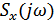
| 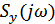
|
Функция плотности вероятностей: 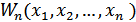
| 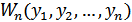
|
Функция распределения вероятностей: 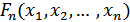
| 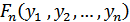
|
Математическое ожидание: 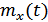
| 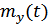
|
Дисперсия: 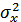
| 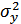
|
Функция корреляции: 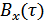
| 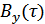
|
Интервал корреляции: 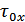
| 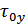
|
Коэффициент корреляции: 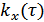
| 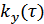
|
Энергетический спектр: 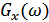
| 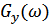
|
Полоса спектра: 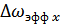
| 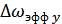
|
Преобразования бывают:
Пассивные преобразования – такое преобразование, в результате которого не возникает новых частот.
Активные преобразования – такое преобразование, в результате которого возникают новые частоты (которых не было в исходном возмущении). Активное преобразование возможно только с использованием нелинейного или параметрического элемента (т.е. возможно только в нелинейных или параметрических цепях).
Рассмотрим нелинейную цепь:
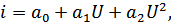
где 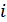 – параметр цепи,
– параметр цепи,
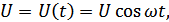
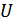 – возмущение (воздействие),
– возмущение (воздействие),
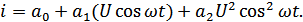
Т.к.
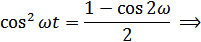
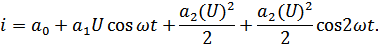
Амплитуда 1-й Постоянная Амплитуда 2-ой
гармоники составляющая гармоники
Иногда появление новых частот является вредным явлением, например, при усилении НЧ сигналов, что приводит к нелинейным искажениям.
Относительный уровень нелинейных искажений определяется коэффициентом гармоник и рассчитывается по формуле:
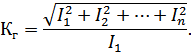
Рисунок 4.6. Спектры токов на входе и выходе НЭ
Рассмотрим воздействие бигармонического колебания на нелинейный элемент:
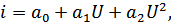
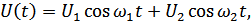
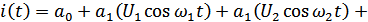
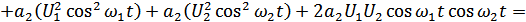
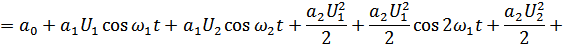
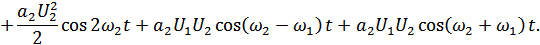
Рисунок 4.7. Спектры напряжений (токов) при воздействии бигармонического колебания на НЭ
Для параметрической цепи:

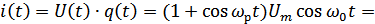
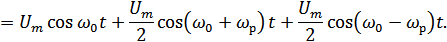
При преобразованиях кроме нелинейных элементов используются фильтры, т.е. линейные элементы.
4.2. Виды преобразования спектров сигнала
1. Умножение частоты – умножение частоты в целое число раз по отношению к частоте входного сигнала.
Рисунок 4.8. Пример умножения частоты на 3
Рисунок 4.9. Функциональные схемы умножителей частоты:
а) на диоде;
б) на транзисторе
2. Деление частоты – получение частоты в  раз меньше, чем частота входного сигнала.
раз меньше, чем частота входного сигнала.
3. Преобразование частоты – суммарно-разностные частоты, получаемые при преобразовании частоты из частот входного сигнала и некоторой частоты вспомогательного сигнала.
Рисунок 4.10. Функциональная схема преобразователя частоты
Рисунок 4.11. Пример преобразования частоты «вверх»
4. Модуляция.
В технике связи сигналы на большие расстояния предаются с помощью модуляции (с использованием для этой цели вспомогательного переносчика) т.е. вспомогательного несущего колебания. При модуляции, как и при преобразовании частоты, происходит перенос низкочастотного (НЧ) спектра в область высоких частот (ВЧ).
Примечание: модулированные колебания меньше искажаются в канале связи, чем НЧ сигналы, т.к. НЧ относительно широкополосные, а модулированные – узкополосные. Таким образом:
1) можно бороться с искажением;
2) при использовании вспомогательного несущего колебания можно осуществлять частотную селекцию, которая используется в многоканальных системах связи, т.к. такие сигналы можно разделять с помощью фильтров.
Модуляция – управление одним (или несколькими) из параметров несущего колебания по закону НЧ сигнала.
АМ ЧМ ФМ
5. Детектирование – это процесс, обратный процессу модуляции.
При детектировании выявляется, по какому закону промодулирован сигнал.
4.3. Амплитудно-модулированные сигналы
При амплитудной модуляции амплитуда высокочастотного (ВЧ) сигнала изменяется по закону передаваемого низкочастотного (НЧ) сигнала.
При модуляции гармоническим колебанием:
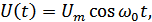
где 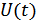 – несущее колебание,
– несущее колебание,
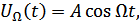
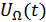 – модулирующее колебание.
– модулирующее колебание.
При АМ:
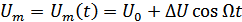 .
.
Если 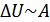 , то:
, то:
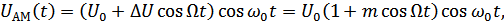
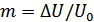 – коэффициент глубины модуляции,
– коэффициент глубины модуляции,
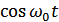 – несущее ВЧ колебание,
– несущее ВЧ колебание,
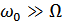 ,
,
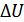 – амплитуда огибающей,
– амплитуда огибающей,
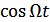 – модулирующее НЧ колебание.
– модулирующее НЧ колебание.
Рисунок 4.12. а) модулирующее колебание;
б) модулированное колебание
Рисунок 4.13. Временные характеристики АМ-колебания при различных 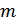
Если модулирующий сигнал более сложной формы (не гармоническое колебание):
Рисунок 4.14. Временные характеристики:
а) модулирующего колебания сложной формы;
б) АМ-колебания
Огибающая изменяется в соответствии с формой модулирующего сигнала.
4.4. Дискретная амплитудная модуляция (ДАМ)
Модулирующее колебание может быть не только непрерывным, но и дискретным. На рис. 4.14 приведен пример модуляции дискретным сигналом.
Рисунок 4.15. Пример ДАМ
Таким образом, под АМ понимается изменение амплитуды ВЧ сигнала переносчика, по закону передаваемого НЧ сигнала.
4.5. Спектральное и векторное представление амплитудно-модулированного сигнала
Спектральное представление:
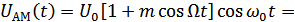
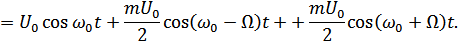
Рисунок 4.16. Спектральное представление АМ-сигнала при модуляции чистым тоном
Ширина спектра АМ сигнала в 2 раза шире спектра передаваемого (модулирующего) сигнала.








