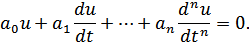Любая непрерывная функция, спектр которой не содержит частот выше , полностью определяется своими отсчетами, взятыми через интервал времени – теорема Котельникова.
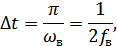
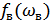– наивысшая частота спектра сигнала.
Рисунок 3.2. а) последовательность отсчетов непрерывной функции;
б) ограничение спектра непрерывной функции
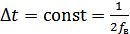– интервал Котельникова,
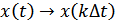– аппроксимирующая функция.
Доказательство: теорема Котельникова основывается на преобразовании Фурье:
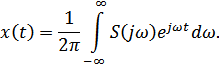
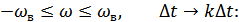
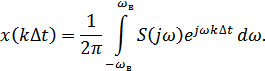
Далее теорема Котельникова основывается на разложении функции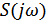 
в комплексный ряд Фурье, на осуществлении перехода от 
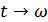, от 
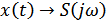и от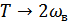 
.
С математической точки зрения теорема Котельникова означает представление сигнала в виде ряда:
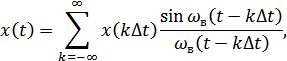
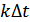– отсчеты, ( 
),
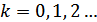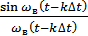– функция отсчетов.
Ряд Котельникова– это разложение сигнала 
в ряд по ортогональным функциям:
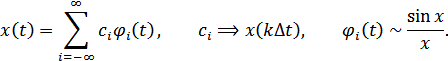
Выводы:
1. Ряд Котельникова является основание для восстановления на приеме непрерывного сигнала по отсчетам.
2. Ряд Котельникова лежит в основе всех импульсных способов передачи сигналов.
ИКМ – импульсно-кодовая модуляция,
АИМ – амплитудно-импульсная модуляция,
ШИМ – широтно-импульсная модуляция,
ФИМ – фазоимпульсная модуляция.
Замечание:
1. 
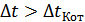– нельзя, т.к.:
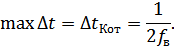
Иначе будет потеряна информация об исходном сообщении.
2. 
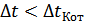можно, но точность передачи не возрастет; если
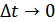, то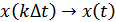 
.
3.1. Восстановление непрерывного сигнала по отсчетам
Для восстановления исходного непрерывного сигнала из импульсов – отсчетов надо эти импульсы подать на вход идеального фильтра нижних частот (ИФНЧ), который имеет следующие характеристики.
Амплитудно-частотная характеристика идеального ФНЧ (АЧХ ИФНЧ) имеет вид:
Рисунок 3.3. АЧХ ИФНЧ
Идеальная реакция ИФНЧ, т.е. реакция на дельта-импульс, имеет вид:
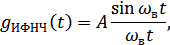
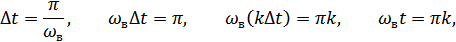
Формула (3.2) определяет точки, где функция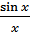 
обращается в ноль.
Спектр на выходе ИФНЧ:
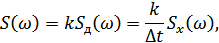
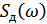– спектр дискретизированного сигнала,
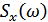– спектр входного воздействия,
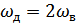– частота дискретизации.
Рисунок 3.4. Импульсная характеристика ИФНЧ
Сущность восстановления исходного сигнала по отсчетам Котельникова показана на рис. 3.5.
Рисунок 3.5. Процесс восстановления сигнала по отсчетам Котельникова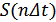 
Таким образом, с точностью до постоянного множителя мы получим на выходе ИФНЧ спектр исходного сигнала. С временной точки зрения мы получим исходный непрерывный сигнал .
3.2. Погрешности дискретизации и восстановления непрерывных сигналов
Теорема Котельникова справедлива только для сигналов с финитным (ограниченным) спектром. На рис. 3.6 показаны некоторые варианты финитных спектров.
Финитный сигнал:
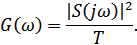
Рисунок 3.6. Пример финитных сигналов (с ограниченным спектром)
Однако спектры реальных информационных сигналов бесконечны. В этом случае Теорема Котельникова справедлива с погрешностью. Погрешность дискретизации определяется энергией спектральных оставляющих сигнала, лежащих за пределами частоты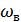 
(рис. 3.7).
Реальный сигнал:
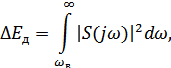
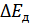– погрешность дискретизации.
Рисунок 3.7. Спектр сигнала, ограниченного ωв
Вторая причина возникновения погрешностей – неидеальность восстанавливающего ФНЧ. При этом нарушается ортогональность функции типа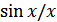 
и происходит смещение нулей.
Таким образом, погрешность дискретизации и восстановление непрерывного сигнала определяется следующими причинами:
1. Спектры реальных сигналов не финитны;
2. АЧХ идеальных ФНЧ неидеальна.
Пример:
Если в качестве ФНЧ использовать RC-фильтр, то восстановленный сигнал на его выходе будет иметь вид, представленный на рис. 3.8, с учетом того, что импульсная реакция RC-фильтра:
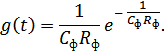
Рисунок 3.8. а) полученный на приеме сигнал;
б) переданный сигнал
Вывод:
Чем выше частота дискретизации 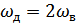и чем ближе спектральная характеристика ФНЧ к идеальной, тем восстановленный сигнал ближе к переданному.
3.3. Структурная схема передачи аналогового сигнала отсчетами Котельникова
На рис. 3.9 изображена структурная схема передачи аналогового сигнала с использованием теоремы Котельникова.
Сообщение от источника преобразовывается в первичный сигнал и поступает на фильтр нижних частот (ФНЧ), который определяет интервал дискретизации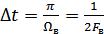 
, где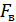 
– частота среза ФНЧ. Далее в дискретизаторе непрерывная функция преобразуются в дискретные отсчеты, которые с помощью переносчика (модулятора) преобразуются в сигнал, согласованный с линией связи. На приемной стороне после демодулятора отсчеты подаются на ФНЧ и далее сообщение поступает к получателю.
Рисунок 3.9. Структурная схема передачи аналогового сигнала отсчетами Котельникова
Временные и спектральные характеристики сигналов в различных точках структурной схемы показаны на рис. 3.10, 3.11.
Рисунок 3.10. Временные и спектральные характеристики сигналов на передающей стороне
Рисунок 3.11. Временные и спектральные характеристики сигналов на приемной стороне (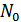 
– спектральная плотность мощности флуктуационной помехи)
4. Методы формирования и преобразования сигналов
4.1. Классификация радиотехнических цепей
Любая радиотехническая (электрическая) цепь описывается дифференциальным уравнением
