Тема урока: Действия над векторами в пространстве.
Группа ПС1-13
Дата: 12.02.22 (2 пара)
Дисциплина: Математика
Тема урока: Действия над векторами в пространстве.
Преподаватель: Старцева М.С.
Тип урока: Урок изучения нового материала и первичного закрепления.
Предыдущее обучение Векторы в пространстве.
Цель урока:
Цели
Образовательные:
- повторение теоретических сведений по теме;
- рассмотрение правил треугольника и параллелограмма сложения векторов в пространстве, законы сложения векторов;
- изучение правил сложения нескольких векторов в пространстве;
- рассмотрение правил умножения вектора на число и основные свойства этого действия.
Развивающие:
- развитие пространственного воображения и логического мышления;
- развитие памяти, математической речи, наблюдательности, развитие графических навыков у учащихся.
Воспитательные:
- воспитание интереса к предмету и потребности в приобретении знаний.
1. Организационный этап.
Ход урока
2. Организационный этап.
Сегодня на уроке мы рассмотрим правила сложения векторов в пространстве, умножение вектора на число.
Давайте вспомним основные понятия, которые нам понадобятся на сегодняшнем уроке.
3. Актуализация опорных знаний.
В левом столбце таблицы – вопросы, в правом – ответы. Установите соответствие.
| Числа, которые определяют положение точки, называются …? | Вектором |
| Векторы называются равными, если… | Координатами |
| Вектора, которые лежат на одной прямой или на параллельных прямых, называются …? | Из координат конца вектора вычесть координаты начала |
| Направленный отрезок называется … | Сонаправленным |
| Чтобы найти координаты вектора нужно …? | Коллинеарными |
| Любая точка пространства может рассматриваться как … вектор | Сонапрвленными и противоположно направленными |
| Вектор называется единичным, если… | Нулевой |
Формула нахождения длины вектора 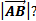
| 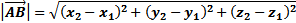
|
| Коллинеарные векторы могут быть … | Его длина равна единице |
| Нулевой вектор принято считать … с любым вектором | Они сонаправлены и их длины равны |
4.Изучение нового материала.
Суммой векторов 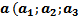 ) и
) и 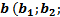
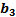 ) называется вектор
) называется вектор 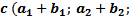
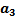 +
+ 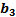 )
)
Правило треугольника.
Сложение и вычитание векторов в пространстве вводится так же, как и на плоскости и подчиняется тем же законам.
Введем правило сложения двух произвольных векторов 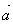 и
и 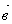 . Отложим от какой-нибудь точки А вектор
. Отложим от какой-нибудь точки А вектор 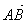 , равный
, равный 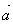 . Затем от точки В отложим вектор
. Затем от точки В отложим вектор 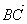 , равный
, равный 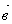 . Вектор
. Вектор 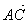 называется суммой векторов
называется суммой векторов 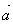 и
и 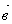 :
: 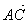 =
= 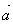 +
+ 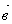 .
.
Это правило сложения векторов называется правилом треугольника.
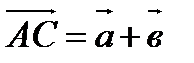
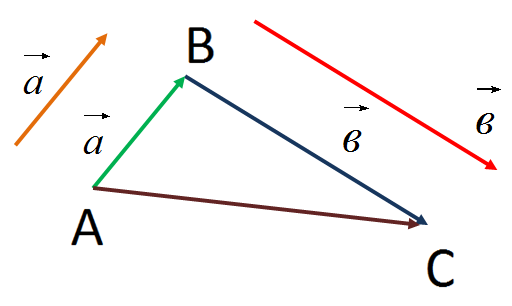
Для любых трех точек А, В и С имеет место равенство 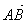 +
+ 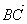 =
= 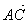 .
.
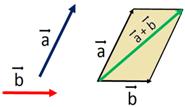
Правило параллелограмма.
Для сложения двух неколлинеарных векторов можно пользоваться также правилом параллелограмма, известным из курса планиметрии. Чтобы сложить два неколлинеарных вектора, нужно отложить их от одной точки и построить на них параллелограмм. Тогда вектор, выходящий из этой же точки, и содержащий диагональ параллелограмма, равен сумме двух данных векторов.
Разность векторов.
Разностью векторов 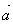 и
и 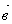 называется такой вектор, сумма которого с вектором
называется такой вектор, сумма которого с вектором 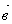 равна вектору
равна вектору 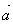 . Разность
. Разность
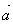 -
- 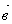 векторов
векторов 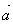 и
и 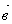 можно найти по формуле
можно найти по формуле 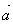 -
- 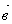 =
= 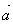 + (-
+ (- 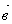 ), где (-
), где (- 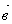 ) – вектор, противоположный вектору
) – вектор, противоположный вектору 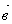 .
. 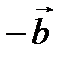
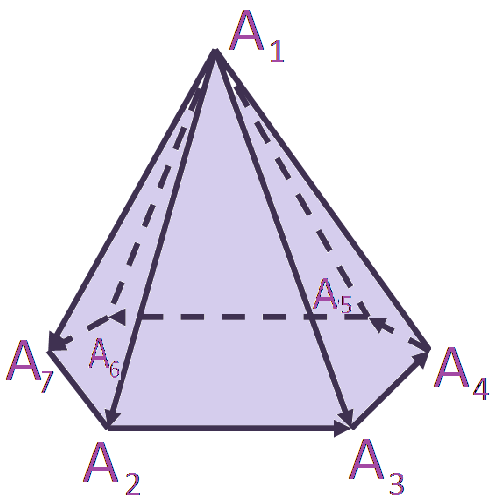
Правило многоугольника.
Сформулируем правило многоугольника. Первый вектор складывается со вторым, затем их сумма — с третьим вектором и т. д. Из законов сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются.
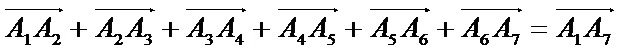
Произведение вектора на число.
Произведением вектора 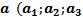 ) на число
) на число 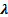 называется вектор
называется вектор 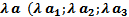 ).
).
Абсолютная величина вектора 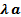 равна
равна 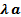 , а направление совпадает с направлением вектора
, а направление совпадает с направлением вектора 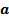 , если
, если 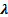 > 0, и противоположно направлению вектора
> 0, и противоположно направлению вектора 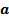 , если
, если 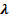 < 0.
< 0.
5.Закрепление изученного материала.
1. Задача.
Дано: 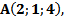
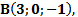
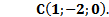
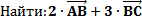
Решение
1) Находим координаты вектора 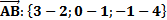
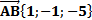 ;
;
2) Затем находим координаты вектора 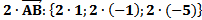
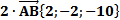
3) Теперь находим аналогично координаты вектора 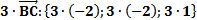
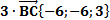
Теперь находим сумму данных векторов, складывая соответствующие координаты: 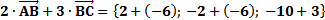
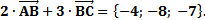
Ответ: 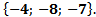
3.Самостоятельная работа
1) Найдите сумму векторов: 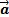 (4;2;-4) и
(4;2;-4) и 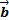 (6;-4 ;10).
(6;-4 ;10).
2) Умножьте вектор 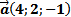 на –3.
на –3.
3) Дано: 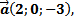
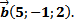 Найдите
Найдите 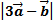
Литература:
Погорелов А.В. Геометрия учеб. для 10-11кл.общеобразовательных учреждений А.В. Погорелов– М.: Просвещение, 2008.
https://vpr-rlass.com/uchebniki/matematika/10-11_klass_pogorelov_uchebnik_chitat_onlajn.html
Ответы предоставить в электронном формате с последующей отправкой на электронную почту: 37 ekaterina 37@ gmail . com








