9. 14. Особенности расчета характеристик асинхронных
ДВИГАТЕЛЕЙ С РОТОРАМИ, ИМЕЮЩИМИ ДВОЙНУЮ БЕЛИЧЬЮ
КЛЕТКУ ИЛИ ФИГУРНЫЕ ПАЗЫ
Необходимость обеспечения высоких пусковых моментов для нормальной работы ряда приводов привела к довольно широкому распространению асинхронных двигателей с роторами, имеющими двойную беличью клетку со вставными стержнями или фигурными пазами, залитыми алюминием. В последние годы получили распространение также двухклеточные роторы с литыми обмотками. Конфигурация и размеры пазов с литыми обмотками не связаны какими-либо ограничениями, налагаемыми сортаментами профильной меди или латуни, поэтому они могут быть выполнены более рационально с точки зрения использования зубцовой зоны ротора и обеспечения высоких пусковых характеристик по сравнению со сварными клетками.
Расчет магнитной цепи двигателей с фигурными стержнями или двойной клеткой на роторе не отличается от расчета обычных асинхронных машин. Некоторая особенность расчета магнитного напряжения зубцовой зоны ротора учтена в расчетных формулах, приведенных в § 9.9.
Здесь и далее фигурный стержень литой обмотки ротора будем рассматривать как двойную клетку ротора, причем к пусковой клетке отнесем верхнюю (прямоугольную или полуовальную — в зависимости от формы фигурного паза) часть стержня, а к рабочей клетке — его нижнюю часть.
Расчет параметров двухклеточного ротора встречает существенные затруднения, так как распределение токов между стержнями верхней и нижней клеток определяется как соотношением их активных сопротивлений, так и частотой тока в роторе. В то же время при больших скольжениях распределение плотности токов в пределах сечений каждого из стержней также неравномерно из-за действия эффекта вытеснения тока.
При расчете параметров двухклеточных роторов применяют приближенные методы, позволяющие получить общее выражение для активного и индуктивного сопротивлений обеих обмоток ротора r2 и х2 с учетом распределения токов между стержнями верхней и нижней клеток в зависимости от скольжения ротора. Это дает возможность проводить расчет рабочих и пусковых характеристик двигателей по формулам, применяемым для расчета характеристик машин с одноклеточными роторами.
Рассмотрим один из таких приближенных практических методов расчета параметров двухклеточного ротора.
Схема замещения фазы двухклеточного ротора представлена на рис. 9.63. Как видно, сопротивления рабочей и пусковой клеток включены параллельно. Ветвь а—б—в содержит
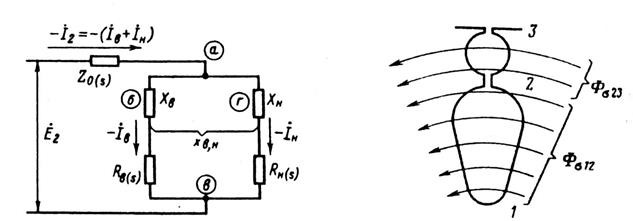
Рис. 9.63. Схема замещения фазы корот- Рис. 9.64. Поток рассеяния в пазу двух-козамкнутого ротора асинхронного дви- клеточного ротора
гателя с двойной беличьей клеткой
сопротивление верхней (пусковой) клетки, ветвь а—г—в сопротивления нижней (рабочей) клетки [6].
Схеме замещения соответствует система уравнений
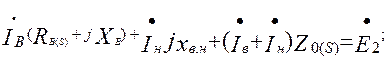 (9.287)
(9.287)
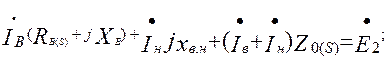
В этих уравнениях и на схеме замещения 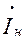 ,
, 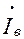 — токи в стержнях верхней и нижней клеток; Rв(s) и Rн(s) — активные, а Хв и Хн - индуктивные сопротивления соответственно верхней и нижней клеток; хн.в = хв.н — сопротивление взаимной индукции между стержнями верхней и нижней клеток; Z0(S) — общее для обеих параллельных ветвей сопротивление.
— токи в стержнях верхней и нижней клеток; Rв(s) и Rн(s) — активные, а Хв и Хн - индуктивные сопротивления соответственно верхней и нижней клеток; хн.в = хв.н — сопротивление взаимной индукции между стержнями верхней и нижней клеток; Z0(S) — общее для обеих параллельных ветвей сопротивление.
Анализируя картину поля потока рассеяния в пазу двухклеточного ротора (рис. 9.64), видим, что часть потока пазового рассеяния Фσ12 сцеплена только со стержнем нижней клетки (участок паза 1-2), Оставшаяся часть потока Ф σ23, магнитные линии которого проходят через паз выше нижнего стержня (участок паза 2-3), сцеплена со стержнями и верхней, и нижней клеток. Поэтому индуктивное сопротивление стержня нижней клетки определяется проводимостью всего потока рассеяния паза, а сопротивление индуктивности верхнего стержня и взаимная индуктивность верхнего и нижнего стержней определяются проводимостью потока Фσ23, так как только эта часть потока сцеплена одновременно и с верхним, и с нижним стержнями.
Исходя из этого, примем следующие обозначения: хп.в — индуктивное сопротивление пазового рассеяния стержня верхней клетки, определяемое проводимостью верхней часта паза λп.в с учетом потокосцепления с верхним стержнем (поток Ф σ23 создается МДС и верхнего, и нижнего стержней); (хн + хв) — индуктивное сопротивление пазового рассеяния стержня нижней клетки, причем хн определяется проводимостью потоку рассеяния Фσ12 нижней части паза с учетом изменяющегося по высоте паза потокосцепления с нижним стержнем, а хв — проводимостью потоку рассеяния Фσ23 верхней части паза. Потокосцепление потока Фσ23 с нижним стержнем постоянно.
Кроме того, учтем, что сопротивление взаимной индукции хв.н = xн.в определяется также проводимостью верхней части паза потоку Фσ23..
Детальный анализ потоков рассеяния и математическое выражение коэффициентов магнитной проводимости, определяющих указанные выше сопротивления, показывают, что для принятых в электромашиностроении конфигураций и размерных соотношений пазов верхней и нижней клеток без большой погрешности в уравнениях (9.287) можно принять Xв ≈ хн.в ≈ хв.н, так как эти сопротивления обусловлены проводимостью верхней части паза и
Хн = хв + хн.
При принятом допущении система уравнений (9.287) может быть записана следующим образом:
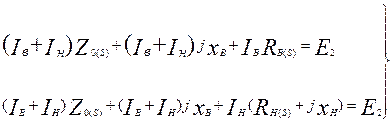 (9.288)
(9.288)
Системе уравнений (9.288) соответствует схема замещения, приведенная на рис. (9.288), которая может служить исходной для определения параметров двухклеточного ротора. Практические формулы дня расчета r2 и х2 роторов с общими и раздельными замыкающими кольцами несколько различаются.
Рассмотрим вначале метод расчета r2 и x2 роторов с общими замыкающими кольцами. Для таких роторов коэффициенты при неизвестных токах в уравнениях (9.288) обозначают следующие сопротивления: RB(s) + rB / s — активное сопротивление стержня верхней клетки; RН(s) = rН / s — активное сопротивление стержня нижней клетки; xв = хп.в — индуктивное сопротивление пазового рассеяния стержня верхней клетки; хн = хп.н — индуктивное сопротивление пазового рассеяния стержня нижней клетки;
Z0(S) = Z кл( s) + j x д
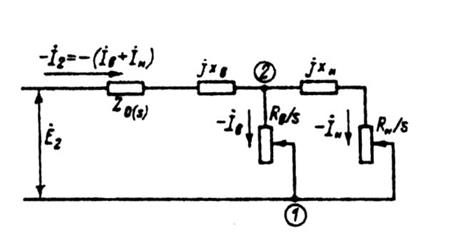
Рис. 9.65. Преобразованная схема замещения фазы
короткозамкнутого ротора с двойной беличьей клеткой
где Zкл(S) — сопротивление участков замыкающих колец между двумя соседними пазами, приведенное к току ротора (см. § 9.10); хд — индуктивное сопротивление дифференциального рассеяния обмотки ротора.
Эквивалентное сопротивление разветвленной цепи этой схемы между токами 1— 2
Z э( s) = 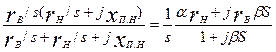 (9.289)
(9.289)
где
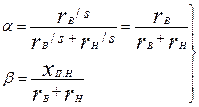 (9.290)
(9.290)
Представим Zэ(s) в виде суммы активного rэ и индуктивного хэ сопротивлений:
Z э( s ) = 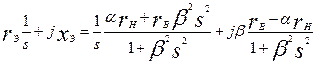
и упростим выражение для rэ и хэ
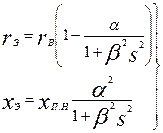 (9.291)
(9.291)
Сопротивления rэ и хэ зависят от скольжения, так как изменение соотношения активных и индуктивных сопротивлений стержней, вызванное изменением частоты тока в роторе, изменяет соотношение токов в стержнях рабочей и пусковой клеток.
При скольжениях s << 1, соответствующих холостому ходу и номинальному режиму двигателей, из (9.291) получим
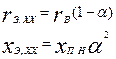
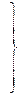 (9.292)
(9.292)
Коэффициенты изменения эквивалентных сопротивлений rэ и xэ в зависимости от скольжения
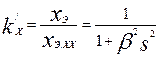 ; (9.293)
; (9.293)
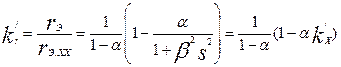 (9.294)
(9.294)
На основании полученных соотношений и с учетом материала § 9.13 запишем основные расчетные формулы для определения r2 и x2 двухклеточных роторов с общими замыкающими кольцами (двухклеточные роторы с литыми обмотками и роторы с фигурными пазами).
При s0 < s ≤ sн активное сопротивление фазы ротора, Ом,
r 2 = r э.х.х + r 0 = r в (1 - α) + 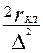 (9.295)
(9.295)
где α — по (9.290), причем
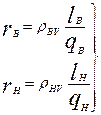 (9.296)
(9.296)
ρBV, ρHV, lV, lH, qB, qH — удельные сопротивления при расчетной температуре, длины и площади поперечных сечений стержней верхней и нижней клеток; при литых обмотках с общими замыкающими кольцами в ρBV = ρHV и, lV =lH; Δ — см. (9.70).
Индуктивное сопротивление фазы ротора, Ом,
x 2 = x п.в + x0 + x э.х.х, (9.297)
где
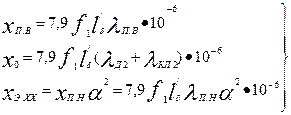 (9.298)
(9.298)
С учетом (9.298)
х2 =7,9 f 1 l ' δ (λп.в + λп.н α2 + λд2 + λкл2) 10-6, (9.299)
где λп.в, и λп.н — коэффициенты магнитных проводимостей потоков пазового рассеяния соответственно верхней и нижней клеток, которые определяются в зависимости от конфигурации пазов верхней и нижней клеток по формулам табл. 9.34; λд2 — коэффициент магнитной проводимости дифференциального рассеяния ротора, который определяется по (9.180); λкл2 = λл2 — коэффициент магнитной проводимости участков замыкающего кольца, приведенный к току ротора, который определяется по (9.178) или по (9.179).
Для пусковых режимов (s ≥ sн)r2ξ и x2ξ роторов с общими замыкающими кольцами рассчитывают по следующим формулам.
Активное сопротивление фазы ротора, Ом,
r2 ξ = r в (1 – α ) k'r + 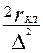 = r в (1 – α k'x) +
= r в (1 – α k'x) + 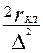 (9.300)
(9.300)
Таблица 9.34. Расчетные формулы для определения коэффициента магнитной
проводимости пазового рассеянна двухклеточных роторов
и роторов с фигурными пазами
| Рисунок
| Расчетные формулы | |
| λП.В | λП.Н | |
| 9.66, а | 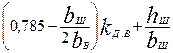
| 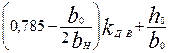
|
| 9.66, б |
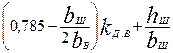
|
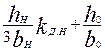
|
| 9.66, в |
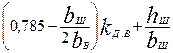
| 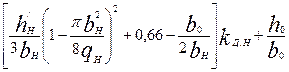
|
| 9.66, г |
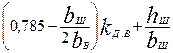
| 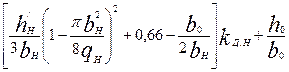
|
| 9.66, д | 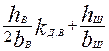
| 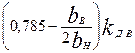
|
| 9.66, е |
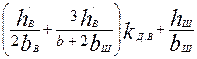
| 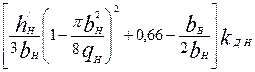
|
Примечания: 1. При закрытых пазах ротора коэффициент магнитной проводимости шлица hш/ bш рассчитывать в соответствии с указаниями, приведенными в § 9.10 (см. рис. 9.52).
2. При расчете параметров холостого хода и номинального режима принимать kд.в = kд.н = 1.
Индуктивное сопротивление фазы ротора, Ом,
х2ξ =7,9 f 1 l ' δ (λп.в + λп.н α2 k ' x + λкл2 + λд) 10-6
В этих формулах k'х и k'r рассчитывают по (9.293) и (9.294), в которых α и β определяют по (9.290), а λп.в и λп.н Для пазов, показанных на рис. 9.66, — по формулам табл. 9.34.
Предполагают, что плотность тока в пределах сечения каждого из стержней постоянна. При ξв > 1 и ξн > 1 можно несколько повысить точность расчета, учитывая влияние эффекта вытеснения тока на сопротивления каждого из стержней. Для этого по формулам, приведенным в § 9.13, последовательно рассчитывают для верхнего стержня ξв, krв, rвξ, kд.в, хвξ и для нижнего стержня ξн, krн, rнξ, kд.н, хп.нξ, после чего определяют
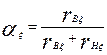
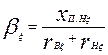 (9.302)
(9.302)
подставляя эти величины вместо α и β последующие формулы, находят k'хξ и k'rξ и по (9.300) и (9.301) рассчитывают r2ξ и х2ξ с учетом влияния эффекта вытеснения тока на сопротивление каждого из стержней обмотки при принятых значениях s. Обычно krв и krн близки к единице, и уточнения расчета, связанного с влиянием эффекта вытеснения тока на каждый из стержней, не требуется.
Для уточнения расчета пускового момента и тока следует учесть также влияние насыщения от полей рассеяния на проводимость паза верхней клетки. Расчет проводят аналогично изложенному в § 9.13.
При расчете сопротивлений роторов с раздельными замыкающими кольцами (двухклеточные роторы с обмоткой из вставных стержней) аналогично принятому ранее допущению (хв.н = хп.в) принимают, что индуктивное сопротивление участков замыкающего кольца верхней клетки приблизительно равно сопротивлению и взаимоиндуктивности участков колец верхней и нижней клеток. Такое допущение позволяет использовать ту же схему замещения (см. рис. 9.65), но с несколько измененными значениями ее параметров. В схеме замещения ротора с раздельными кольцами:
сумма активных сопротивлений стержня и участков замыкающих колец верхней клетки
Rв = rв + 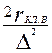 (9.303)
(9.303)
сумма активных сопротивлений стержня и участков замыкающих колец нижней клетки
Rн = rн + 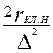 (9.304)
(9.304)
сумма индуктивных сопротивлений пазового рассеяния и участков замыкающих колец верхней клетки
хв = хп.в + хкл.в = 7,9 f 1 l ' δ (λп.в + λкл .в)10 -6 ; (9.305)
сумма индуктивных сопротивлений пазового рассеяния и участков замыкающих колец нижней клетки
хн = хп.н + хкл.н =7,9 f 1 l ' δ (λп.н + λкл .н)10 -6 . (9.306)
В этих выражениях λп.в и λп.н — коэффициенты магнитной проводимости пазового рассеяния соответственно верхней и нижней клеток (рассчитываются в зависимости от конфигурации пазов по данным табл. 9.33); λкл.в, λкл.н — коэффициенты магнитной проводимости участков замыкающих колец [рассчитываются по (9.178) или (9.179)].
Общее сопротивление для обеих параллельных ветвей схемы замещения
z 0 = х0 = хд = 7,9 f 1 l ' δ λД 10 -6., (9.307)
где λд — коэффициент магнитной проводимости дифференциального рассеяния, рассчитываемый по (9.180).
Сопротивления r2 и х2 роторов с раздельными замыкающими кольцами для холостого хода и номинального режима работы, Ом,
r2 = r э . х . х = R в (1 – α ); (9.308)
х 2 = хв + хэ . х . х + х 0 =7,9 f1 l'δ ( λп . в + λп . н α 2 + λкл . в + λд ) 10-6 , (9.309)
где
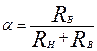
Сопротивления r2ξ и x2ξ, для пусковых режимов работы (s >> sн), Ом,
r 2 ξ = r э = R в (1 – αk'х); (9.310)
х2ξ = 7,9 f 1 l ' δ (λп.в + λп.н α2 k ' x + λкл.в + λд) 10-6, (9.311)
где k'x определяется по (9.293) при
β = Хн / ( R в + R н ). (9.312)
Эффект вытеснения тока в каждом из стержней и влияние насыщения полями рассеяния на параметры ротора учитывают так же, как и для роторов с общими замыкающими кольцами.
Приведенный метод расчета параметров двухклеточных роторов и роторов с фигурными пазами, как и другие аналогичные ему методы, учитывающие индуктивную связь только между полными токами каждого из стержней, являются приближенными, однако они находят применение в расчетной практике благодаря своей простоте. Более точный метод расчета параметров ротора с произвольной конфигурацией стержней рассматривается в спецкурсах [7].
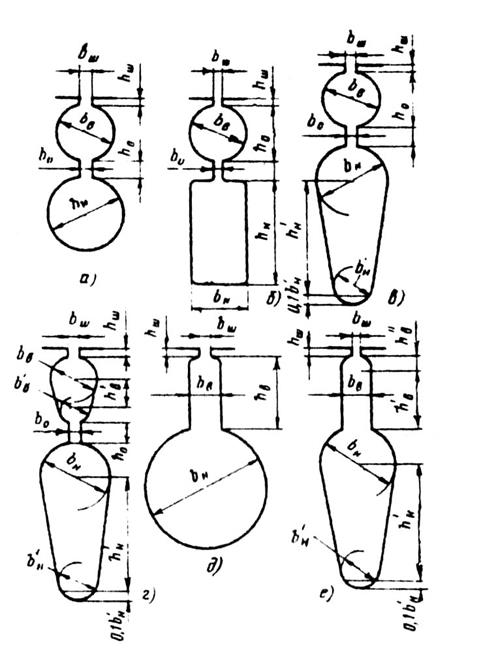
Рис. 9.66. К расчету коэффициентов магнитной
проводимости пазового рассеяния двухклеточных
короткозамкнутых роторов с двойной беличьей клеткой
и с фигурными пазами:
а—г — пазы роторов с двойной беличьей клеткой;
д, е — фигурные пазы

9.15. ОСОБЕННОСТИ ТЕПЛОВОГО И ВЕНТИЛЯЦИОННОГО
РАСЧЕТОВ АСИНХРОННЫХ ДВИГАТЕЛЕЙ
На первоначальной стадии проектирования достаточно достоверную оценку теплового режима двигателя дает приближенный метод теплового расчета, основанный на упрощенном представлении о характере тепловых связей между элементами электрической машины. В нем используют средние значения коэффициентов теплоотдачи с поверхности и теплопроводности изоляции, характерные для определенной конструкции и технологии производства двигателей данного типа.
Для расчета нагрева асинхронных машин, спроектированных на базе серий 4А и АИ, берутся усредненные коэффициенты теплоотдачи с поверхности и теплопроводности изоляции в пазовой и лобовой частях обмоток.
Расчет нагрева проводят, используя значения потерь, полученных для номинального режима, но потери в изолированных обмотках статора и фазного ротора несколько увеличивают по сравнению с расчетными, предполагая, что обмотки могут быть нагреты до предельно допустимой для принятого класса изоляции температуры: при классе нагревостойкости изоляции В — до 120° С, при классе нагревостойкости изоляции F — до 140° С и при классе нагревостойкости изоляции Н — до 165° С. При этом коэффициент увеличения потерь kp по сравнению с полученными для расчетной температуры составит для обмоток с изоляцией класса нагревостойкости В kp = р120/р75 = 1,15, для обмоток с изоляцией класса нагревостойкости F kp = p140/p115 = 1,07, для обмоток с изоляцией класса нагревостойкости Н kp = p165/p115 = 1,45.
Электрические потери в обмотке статора делятся на потери в пазовой части Р'э.п, и потери в лобовых частях катушек Р'э.л1:
Р'э.п = kp P э1 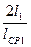 ; (9.313)
; (9.313)
Р'э.л1 = kp P э1 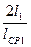 (9.314)
(9.314)
Превышение температуры внутренней поверхности сердечника статора над температурой воздуха внутри машины, ° С,
Δυпов1 = К 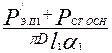 (9.315)
(9.315)
где α1 — коэффициент теплоотдачи с поверхности, определяемый по рис. 9.67 и 9.68 в зависимости от исполнения машины; К — коэффициент, учитывающий, что часть потерь в сердечнике статора и в пазовой части обмотки передается через станину непосредственно в окружающую среду (принимают по табл. 9.35).
Таблица 9.35 Средние значения коэффициента К
| Исполнение двигателя по способу зашиты | Число полюсов двигателя 2р | |||||
| 2 | 4 | 6 | 8 | 10 | 12 | |
| IP44 | 0,22 | 0,20 | 0,19 | 0,18 | 0,17 | 0,16 |
| IP23 | 0.84 | 0.80 | 0,78 | 0,76 | 0.74 | 0.72 |
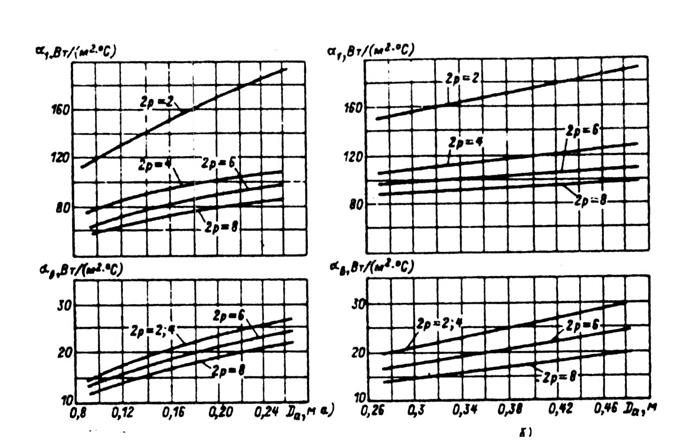
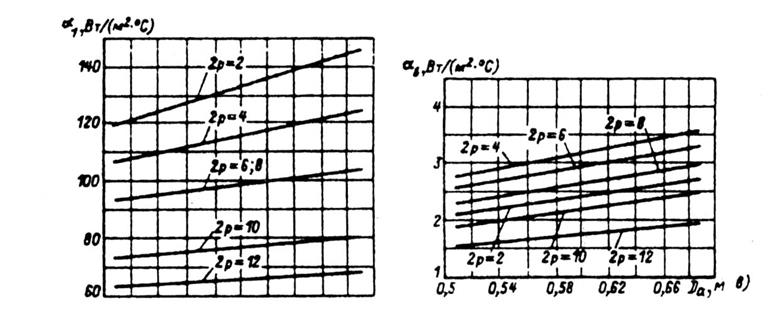
Рис. 9.67. Средние значения коэффициентов теплоотдачи с поверхности α1
и подогрева воздуха αв, для асинхронных двигателей исполнения IP44:
а — при h < 160 мм; б — при h = 160...250 мм; в — при h ≥ 280 мм (для двигателей с продуваемым ротором)
Перепад температуры в изоляции пазовой части обмотки статора,°С,

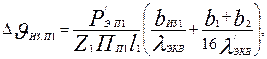 (9.316)
(9.316)
где Пп1 — расчетный периметр поперечного сечения паза статора, равный для полузакрытых трапецеидальных пазов (см. рис. 9.29, а):
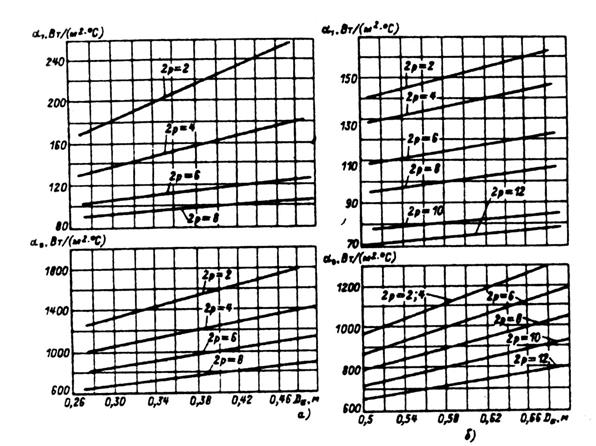
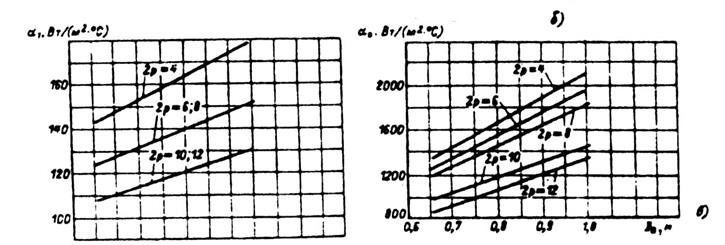
Рис. 9.68. Средние значения коэффициентов теплоотдачи с поверхности α1
и подогрева воздуха αв для асинхронных двигателей исполнения IP23:
а — при h = 160...250 мм, Uном = 660 В;
б — при h ≥ 280 мм,Uном = 660 В;
в — при Uном = 6000 В
Пп1 = 2 h п.к + b 1 + b 2 (9.317)
(hп.к, b1, b2 — размеры паза в штампе); для прямоугольных открытых и полуоткрытых пазов (см. рис. 9.28):
Пп1 = 2( h п + b п );
bиз1 — односторонняя толщина изоляции в пазу; для всыпной обмотки bиз1 берется по соответствующим таблицам (см. гл. 3). Для обмоток из прямоугольного провода
b из1 = ( b п - n эл b )0,5 (9.318)
где nэл и b — число и ширина неизолированных элементарных проводников, расположенных в одном слое по ширине паза; λэкв — средняя эквивалентная теплопроводность пазовой изоляции; для классов нагревостойкости В, F и Н λэкв = 0,16 Вт/(м°С); λ'экв, — среднее значение коэффициента теплопроводности внутренней изоляции катушки всыпной обмотки из эмалированных проводников с учетом неплотности прилегания проводников друг к другу; значение λ'экв берется по рис. 9.69; для обмоток из прямоугольного провода в (9.316) принимают 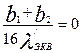
Перепад температуры по толщине изоляции лобовых частей
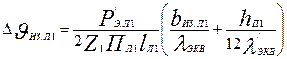 , (9.319)
, (9.319)
где Пл1 — периметр условной поверхности охлаждения лобовой части одной катушки; Пл1 ≈ Пп1; bиз.л1 — односторонняя толщина изоляции лобовой части катушки (по табл. гл. 3). При отсутствии изоляции в лобовых частях bиз.л1 = 0; λ  'экв для всыпной обмотки определяется по рис. 9.69. Для катушек из прямоугольного провода принимают hп1/(12 λ'экв) = 0.
'экв для всыпной обмотки определяется по рис. 9.69. Для катушек из прямоугольного провода принимают hп1/(12 λ'экв) = 0.
Превышение температуры наружной поверхности изоляции лобовых частей обмотки над температурой воздуха внутри машины, ° С,
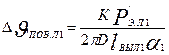 (9.320)
(9.320)
Среднее превышение температуры обмотки статора над температурой воздуха внутри машины, ° С,
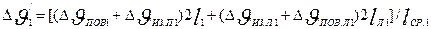 (9.321)
(9.321)
Превышение температуры воздуха внутри машины над температурой окружающей среды определяется в предположении, что температура корпуса равна температуре воздуха внутри машины. При этом условии
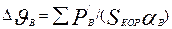 (9.322)
(9.322)
где 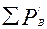 — сумма потерь, отводимых в воздух внутри двигателя, Вт; αВ — коэффициент подогрева воздуха, Вт/(м2•С), учитывающий теплоотдающую способность поверхности корпуса и интенсивность перемешивания воздуха внутри машины (см. рис. 9.67, 9.68); Sкор -эквивалентная поверхность охлаждения корпуса, м2. Для двигателей со степенью защиты IP23
— сумма потерь, отводимых в воздух внутри двигателя, Вт; αВ — коэффициент подогрева воздуха, Вт/(м2•С), учитывающий теплоотдающую способность поверхности корпуса и интенсивность перемешивания воздуха внутри машины (см. рис. 9.67, 9.68); Sкор -эквивалентная поверхность охлаждения корпуса, м2. Для двигателей со степенью защиты IP23
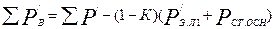 , (9.323)
, (9.323)
где
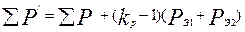 ; (9.324)
; (9.324)
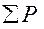 — сумма всех потерь в двигателе при номинальном режиме и расчетной температуре.
— сумма всех потерь в двигателе при номинальном режиме и расчетной температуре.
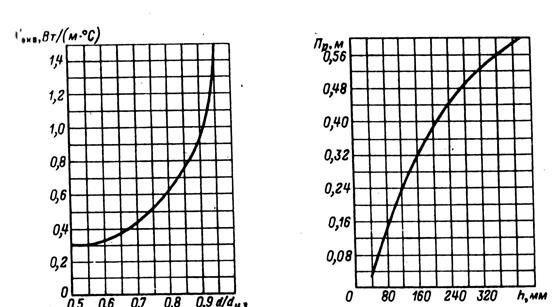
Рис. 9.69. Средние значения коэффи- Рис. 9.70. Средние значения периметра
циентов теплопроводности λ'экв внут- поперечного сечения ребер корпуса
ренней изоляции в катушках обмотки из асинхронных двигателей
круглого эмалированного провода
Эквивалентная поверхность охлаждения корпуса, м2,
S кор = π Da ( l 1 + 2 l выл1 ). (9.325)
Для двигателей со степенью защиты IP44 при расчете ∑Р'в не учитывают также мощность, потребляемую наружным вентилятором, которая составляет примерно 0,9 суммы полных механических потерь:
∑Р'в = ∑Р' - (1 - К)(Р'э.п1 + Pст.осн) - 0,9Рмех, (9.326)
где ∑Р' —по (9.324).
При расчете Sкор учитывают поверхность ребер станины:
S к op =( π Da + 8 Пр )(l1 + 2l выл 1 ), (9.327)
где Пр—условный периметр поперечного сечения ребер корпуса двигателя; значение Пр может быть принято приближенно по кривой рис. 9.70.
Среднее превышение температуры обмотки статора над температурой окружающей среды,°С,
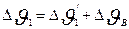 , (9.328)
, (9.328)
Из-за приближенного характера расчета 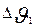 , должно быть, по крайней мере, на 20 % меньше, чем допускаемое превышение температуры для принятого класса изоляции (см. табл. 7.1).
, должно быть, по крайней мере, на 20 % меньше, чем допускаемое превышение температуры для принятого класса изоляции (см. табл. 7.1).
Превышение температуры обмотки фазного ротора определяется аналогично в следующей последовательности.
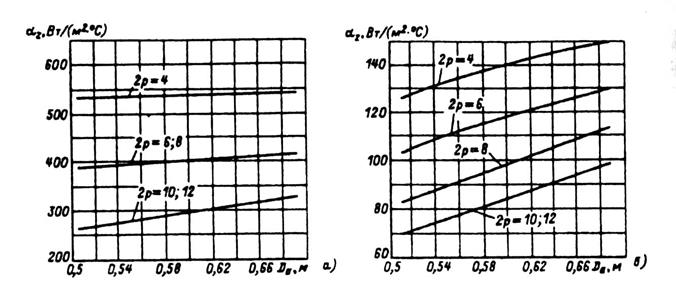
Рис. 9.71. Средние значения коэффициента теплоотдачи с
поверхности от фазных роторов асинхронных двигателей с Uном = 660 В:
а — исполнения IP44 с продуваемым ротором; б — исполнения IP23
Превышение температуры магнитопровода ротора над температурой воздуха внутри машины,°С,
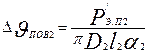 , (9.329)
, (9.329)
где α2 — коэффициент теплоотдачи, определяемый по рис. 9.71 и 9.72; Р'э.п2 — электрические потери в пазовой части обмотки ротора:
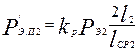 (9.330)
(9.330)
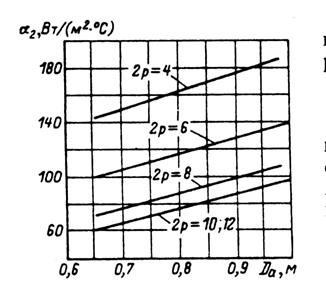
Рис. 9.72. Средние значения коэффициентов теплоотдачи
с поверхности α2 фазных роторов асинхронных
двигателей с Uном = 6000 В исполнения IP23
Перепад температуры в изоляции пазовой части обмотки ротора, °С
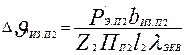 , (9.331)
, (9.331)
где Пп2 — периметр паза ротора. Для прямоугольных пазов
Пп2 = 2( h п2 + b п2 ). (9.332)
Превышение температуры наружной поверхности лобовых частей над температурой воздуха внутри машины, ° С,
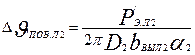 , (9.333)
, (9.333)
где Р'эл2 — электрические потери в лобовых частях обмотки, Вт:
Р'эл2 = k р РЭ1 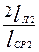 (9.334)
(9.334)
Перепад температуры в изоляции лобовых частей обмотки ротора, ° С,
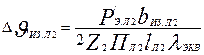 (9.335)
(9.335)
где Пл2 — периметр поперечного сечения условной поверхности охлаждения лобовой части одной катушки: Пл2 = Пп2; bиз.л2 — односторонняя толщина изоляции лобовых частей (по табл. гл. 3).
Среднее превышение температуры обмотки ротора над температурой воздуха внутри двигателя, ° С,
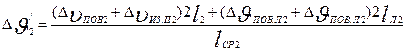 (9.336)
(9.336)
Среднее превышение температуры обмотки ротора над окружающей средой, ° С,
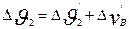 . (9.337)
. (9.337)
Вентиляционный расчет асинхронных двигателей, так же как и тепловой на первоначальном этапе проектирования, может быть выполнен приближенным методом, который заключается в сопоставлении расхода воздуха, необходимого для охлаждения двигателя и расхода, который может быть получен при данной конструкции и размерах двигателя.
Для двигателей со степенью защиты IP23 требуемый для охлаждения расход воздуха, м3/с,
Q в = ∑Р'в / (1100 Δ 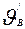 ), (9.338)
), (9.338)
где ∑Р'в — по (9.326); Δ 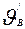 — превышение температуры выходящего из двигателя воздуха над температурой входящего; приближенно Δ
— превышение температуры выходящего из двигателя воздуха над температурой входящего; приближенно Δ 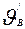 = 2 Δv'в, где Δv'в — по (9.322).
= 2 Δv'в, где Δv'в — по (9.322).
Расход воздуха, который может быть получен при данных размерах двигателя, оценивается по эмпирической формуле
Q' в = m'(n к b к + 0,1) 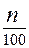 D2a, (9.339)
D2a, (9.339)
где nк и bк — число и ширина, м, радиальных вентиляционных каналов; n — частота вращения двигателя, об/мин; m' — коэффициент (m' — 2,6 для двигателя с 2р = 2; m' = 3,15 для двигателя с2р ≥ 4).
Формула (9.339) приближенно учитывает суммарное действие всех нагнетательных элементов в двигателе: лопаток на замыкающих кольцах литой клетки, вылетов стержней при сварных клетках короткозамкнутых роторов, лобовых частей фазных роторов, вентиляционных распорок в радиальных каналах и др.
Для двигателей со степенью защиты IP44 требуемый для охлаждения расход воздуха, м3/с,
Q в = km ∑Р'в /(1100 Δ 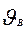 ) , (9.340)
) , (9.340)
где km — коэффициент, учитывающий изменение условий охлаждения по длине поверхности корпуса, обдуваемого наружным вентилятором:
km = m ' 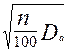 (9.341)
(9.341)
Коэффициент m' = 2,6 для двигателей с 2р = 2 при h ≤ 132 мм и m' = 3,3 при h ≥ 160 мм; m' = 1,8 для двигателей с 2р ≥ 4 при h ≤ 132 мм и m' = 2,5 при h ≥ 160 мм.
Расход воздуха, м3/с, обеспечиваемый наружным вентилятором, может быть приближенно определен по следующей формуле:
Q'в =0,6 D3а 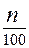 . (9.342)
. (9.342)
Расход воздуха Q'в должен быть больше требуемого для охлаждения машины Qв.
На этом, если не требуется более детального определения температуры отдельных элементов, расчет асинхронного двигателя может быть закончен. Для уточненного расчета теплового режима двигателя могут быть использованы методы, рассмотренные в гл. 7.
9.16. ПРИМЕРЫ РАСЧЕТА
9.16.1 Расчет асинхронного двигателя с короткозамкнутым ротором
Техническое задание
Спроектировать асинхронный трехфазный двигатель с короткозамкнутым ротором: Р2 = 15 кВт, U = 220/380 В, 2р = 4; конструктивное исполнение IM 1001; исполнение по способу защиты IP44; способ охлаждения IC0 141; климатическое исполнение и категория размещения УЗ, класс нагревостойкости изоляции F.
Выбор главных размеров
1. Высота оси вращения (предварительно) по рис. 9.18, a h = 0,17 м. Принимаем ближайшее стандартное значение h = 160 мм; Da = 0,272 м (см. табл. 9.8).
2. Внутренний диаметр статора D = kD Da = 0,68 • 0,272 = 0,185 м, kD = по табл. 9.9.
3. Полюсное деление τ = π D/(2p) = π 0,185/4 = 0,145 м.
4. Расчетная мощность по (9.4)
P ' = mIE = P 2 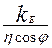 =
= 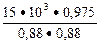 = 18 885 ≈ 18 900 В
= 18 885 ≈ 18 900 В  А
А
(kE — по рис. 9.20; η и cos φ— по рис. 9.21, а).
5. Электромагнитные нагрузки (предварительно по рис. 9.22, б)
А = 32 • 103 А/м; Вδ = 0,75 Тл
6. Обмоточный коэффициент (предварительно для однослойной обмотки) kоб1 = 0,95.
7. Расчетная длина магнитопровода по (9.6)
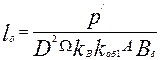 =
= 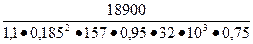 = 0,139 ≈ 0,14 м
= 0,139 ≈ 0,14 м
(по (9.5) Ω = 2nf / p = 2n • 50/2 = 157 рад/с].
8. Отношение λ = lδ /τ = 0,14/0,145 = 0,97. Значение λ = 0,97 находится в допустимых пределах (см. рис. 9.25).
Определение Z1, w1 и площади поперечного сечения провода обмотки статора
9. Предельные значения tz1 (по рис. 9.26): tz1max = 15 мм; tz1min = 12 мм.
10. Число пазов статора по (9.16)
Z1min = 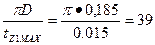
Z2max = 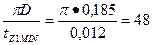
Принимаем Z1 = 48, тогда q1 = Z1/(2pm) - 48/(4 • 3) = 4. Обмотка однослойная.
11 . Зубцовое деление статора (окончательно)
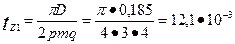 м
м
12. Число эффективных проводников в пазу [предварительно, при условии а = 1 по (9.17)]
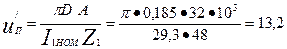
(по 9.18)
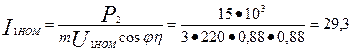 А
А
13. Принимаем а = 1, тогда по (9.19) u п = а u 'п = 13 проводников.
14. Окончательные значения:
число витков в фазе по (9.20)
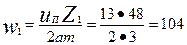
линейная нагрузка по (9.21)
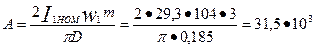 А/м
А/м
магнитный поток по (9.22)
Ф = 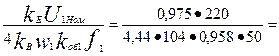 9,7
9,7  10-3 Вб
10-3 Вб
(для однослойной обмотки с q = 4 по табл. 3.16 kоб1 = kp1 = 0,958; для Da = 0,272 м по рис. 9.20 kE = 0,975);
индукция в воздушном зазоре по (9.23)
Вδ = 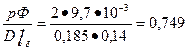 Тл
Тл
Значения А и Вδ находятся в допустимых пределах (см. рис. 9.22, б).
15. Плотность тока в обмотке статора (предварительно) по (9.25). А по п. 14 31,5  103 А/м
103 А/м
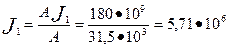 А/м2
А/м2
(AJ1 = 180  109 по рис. 9.27, б).
109 по рис. 9.27, б).
16. Площадь поперечного сечения эффективного проводника (предварительно) по (9.24), а = 1.
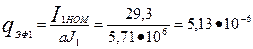 м2 =5,13 мм2.
м2 =5,13 мм2.
17.Сечение эффективного проводника (окончательно): принимаем nэл = 3, тогда qэл = qэф/nэф = 5,13/3 = 1,71 мм2. Принимаем обмоточный провод марки ПЭТВ (см. приложение 3), dэл = 1,5 мм, qэл = 1,767 мм2, qэ.ср = nэл qэл = 3 • 1,767 = 5,3 мм2.
18. Плотность тока в обмотке статора (окончательно) по (9.27)
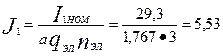 А/мм2.
А/мм2.
Расчет размеров зубцовой зоны статора и воздушного зазора
Паз статора определяем по рис. 9.29, а с соотношением размеров, обеспечивающих параллельность боковых граней зубцов.
19. Принимаем предварительно по табл. 9.12 Вz1 = 1,9 Тл; Ва = 1,6 Тл, тогда по (9.37)
bZ1 = 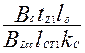 =
= 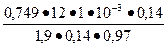 = 4,9•10-3 м = 4,9 мм
= 4,9•10-3 м = 4,9 мм
(по табл. 9.13 для оксидированной стали марки 2013 kc = 0,97);
по (9.28)
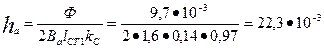 м = 22,3 мм.
м = 22,3 мм.
20. Размеры паза в штампе: bш = 3,7 мм; hш = 1 мм; 45° (см. рис. 9.29, а);
по (9.38)
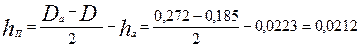 м = 21,2 мм;
м = 21,2 мм;
по (9.40)
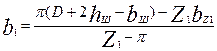 =
= 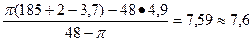 мм
мм
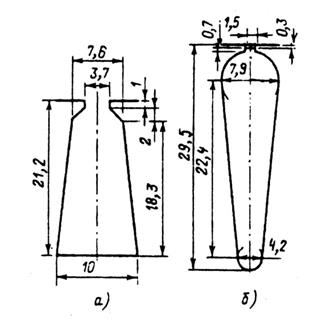
Рис. 9.73. Пазы спроектированного двигателя с короткозамкнутым
ротором (Р2 =15 кВт, 2р = 4, Uном =220/380 В)
по (9.39)
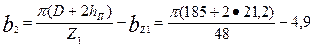 = 9,98 = 10 мм2;
= 9,98 = 10 мм2;
по (9.42)—(9.45)
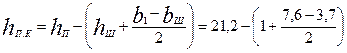 = 18,25 ≈ 18,3 мм
= 18,25 ≈ 18,3 мм
Паз статора показан на рис. 9.73, а.
21. Размеры паза в свету с учетом припуска на сборку:
b'1 = b1 – Δ bп = 7,6 – 0,2 = 7,4 мм
b'2 = b2 – Δ bп = 10 – 0,2 = 9,8 мм
b'п.к = hп.к – Δh = 18,3 – 0,2 = 18,1 мм.
Площадь поперечного сечения паза для размещения проводников обмотки по (9.48)
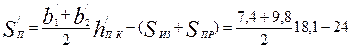 = 131,7 мм2
= 131,7 мм2
[площадь поперечного сечения прокладок Sпр = 0; площадь поперечного сечения корпусной изоляции в пазу
Sиз = bиз(2hп + b1 + b2) = 0,4(2•21,2 + 7,6 + 10) = 24 мм2,
гдe односторонняя толщина изоляции в пазу bиз = 0,4 мм — по табл. 3.1].
22. Коэффициент заполнения паза по (3.2):
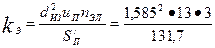 = 0,74
= 0,74
Полученное значение kз допустимо для механизированной укладки обмотки.
Расчет ротора
23. Воздушный зазор (по рис. 9.31) δ = 0,5 мм.
24. Число пазов ротора (по табл. 9.18) Z2 = 38.
25. Внешний диаметр ротора D2 = D - 2δ = 0,185 - 2 • 0,5 • 10-3 = 0,184 м.
26. Длина магнитопровода ротора l2 = l1 = 0,14 м.
27. Зубцовое деление ротора
tz2 = πD2/Z2 =π 0,184/38 = 0,0152 м = 15,2 мм.
28.Внутренний диаметр ротора равен диаметру вала, так как сердечник ротора непосредственно насаживается на вал; по (9.102)
Dj = DB = kBDa = 0,23•0,272 = 0,0626 м ≈ 60 мм
(kB, — по табл. 9.19).
29. Ток в обмотке ротора по (9.57)
I2 = ki I1 vi = 0,904 • 29,3 • 15,73 = 417 А,
где по (9.58) ki = 0,2 + 0,8 cos φ = 0,2 + 0,8 • 0,88 = 0,904;
по (9.66)
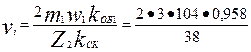 = 15,73
= 15,73
(пазы ротора выполняем без скоса — kск = 1)
30. Площадь поперечного сечения стержня (предварительно) по (9.68)
qп = I 2 / J 2 = 417/(2,5 • 106) = 166,8 • 10 -6 м2 = 166,8 мм2
(плотность тока в стержне литой клетки принимаем J2 = 2,5 • 106 А/м2).
31. Паз ротора определяем по рис. 9.40, б. Принимаем bш = 1,5 мм; hш = 0,7 мм; h'Ш = 0,3 мм.
Допустимая ширина зубца по (9.75)
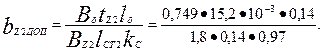 = 6,52•10 -3 м = 6,5 мм
= 6,52•10 -3 м = 6,5 мм
(принимаем ВZ2 = 1,8 Тл по табл. 9.12).
Размеры паза (см. рис. 9.40):
по (9.76)
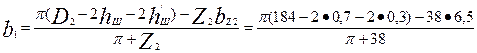 = 7,9 мм
= 7,9 мм
по (9.77)
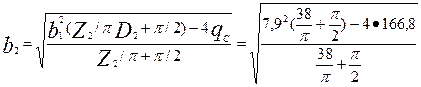 = 4,2 мм
= 4,2 мм
по (9.78)
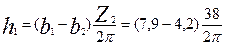 =22,38 ≈ 22,4 мм.
=22,38 ≈ 22,4 мм.
32. Уточняем ширину зубцов ротора по формулам табл. 9.20:
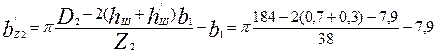 = 6,49мм ≈ 6,5 мм;
= 6,49мм ≈ 6,5 мм;
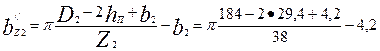 = 6,5 мм
= 6,5 мм
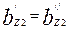 ≈ 6,5 мм
≈ 6,5 мм
Принимаем (см. рис. 9.73, б) b1= 7,9; b2 = 4,2 мм; h1 = 22,4 мм.
Полная высота паза
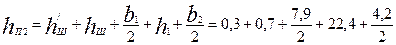 = 29,5 мм
= 29,5 мм
33. Площадь поперечного сечения стержня по (9.79)
qc = 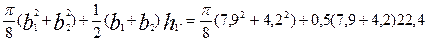 =166,96 ≈167 мм2.
=166,96 ≈167 мм2.
Плотность тока в стержне
J2 = I2/qс = 417/167 • 10 -6 = 2,5 • 106 А/м.
34. Короткозамыкающие кольца (см рис. 9.37, б). Площадь поперечного сечения кольца по (9.72)
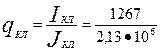 = 595 мм2
= 595 мм2
По (9.70) и (9.71)
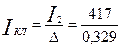 =1267 А
=1267 А
где
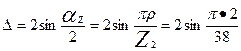 = 0,329 А
= 0,329 А
Jкл = 0,85 J2 = 0,85•2,5•106 = 2,13 • 106 А/м2
Размеры короткозамыкающих колец:
hкл = 1,25 hп2 = 1,25•29,5 = 37 мм;
bкл = qкл / hкл = 595/37 = 16 мм;
qкл = hкл / bкл = 37 • 16 = 592 мм2;
Dк.ср = D2 – hкл = 184 – 37 = 147 мм.
Расчет магнитной цепи
Магнитопровод из стали 2013; толщина листов 0,5 мм.
35. Магнитное напряжение воздушного зазора по (9.103)
Fδ = 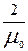 Вδδkδ = 1,59
Вδδkδ = 1,59  106
106  0,749
0,749  1,22
1,22  0,510-3 = 726,5 А ,
0,510-3 = 726,5 А ,
по(4.15)
kδ = 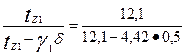 = 1,22,
= 1,22,
где
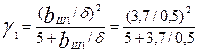 =4,42
=4,42
36. Магнитное напряжение зубцовой зоны статора по (9.104)
FZ1 = 1hz1Hz1 = 2 • 21,2 • 10-3 • 2070 = 87,8 А,
где hZ1 = Hп1 = 21,2 мм (см п. 20 расчета);
расчетная индукция в зубцах по (9.105)
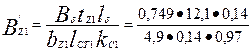 =1,91 Тл
=1,91 Тл
(bz1 = 4,9 мм по п. 19 расчета; kc1, = 0,97 по табл. 9.13). Так как B'z1 > 1,8 Тл, необходимо учесть ответвление потока в паз и найти действительную индукцию в зубце ВZ1. Коэффициент kПХ по высоте hzх = 0,5 hz по (4.33)
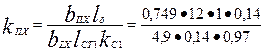 =1,85
=1,85
где
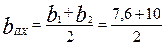 =8,8
=8,8
по (4.32)
BZ1 = B'z1 – μ0 HZ1 kПХ
Принимаем Bz1 = 1,9 Тл, проверяем соотношение BZ1 и B'z1:
1,9 = 1,91 - 1,256 • 10-6 • 2070 • 1,85 = 1,9,
где для Bz1 = 1,9 Тл по табл. П1.7 HZ1 = 2070 А/м.
37. Магнитное напряжение зубцовой зоны ротора по (9.108)
FZ2 = 2hz2 Hz2 = 2 • 0,029 • 1570 = 91,1 А
при зубцах по рис. 9.40, б из табл. 9.20 hz2 = hП2 - 0,1 b2 = 29,4 - 0,1 • 4,2 = 29 мм;
индукция в зубце по (9.109)
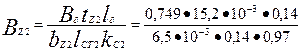 =1,81 Тл
=1,81 Тл
по табл. П1.7 для ВZ2 = 1,81 Тл находим НZ2 = 1570 А/м
38. Коэффициент насыщения зубцовой зоны по (9.115)
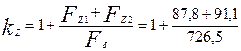 =1,25
=1,25
39. Магнитное напряжение ярма статора по (9.116)
F = LаНa = 0,196  750 = 147 А,
750 = 147 А,
по (9.119)
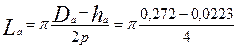 =0,196 м;
=0,196 м;
где
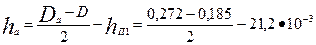 =22,3
=22,3  10-3 м;
10-3 м;
no (9.117)
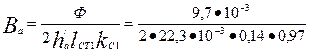 =1,6 Тл
=1,6 Тл
(при отсутствии радиальных вентиляционных каналов в статоре h'a = hа = 22,3 • 10-3 м), для Ва = 1,6 Тл по табл. П1.6 находим На = 750 А/м.
40. Магнитное напряжение ярма ротора по (9.121)
Fj = Lj Hj = 72,7 • 10-3 • 155 = 11,3 А.
По (9. 127)
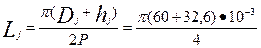 =72,7
=72,7  10-3 м;
10-3 м;
где
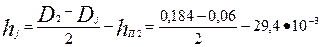 =32,6
=32,6  10-3 м;
10-3 м;
по (9.122)
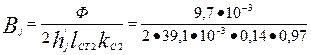 =0,91 Тл
=0,91 Тл
где по (9.124) для четырехполюсных машин при 0,75 (0,5 D2 - hп2) < Dj
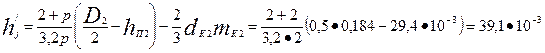 м,
м,
где для mК2 = 0,91 Тл по табл. П1.6 находим Hj = 155 А/м.
41. Магнитное напряжение на пару полюсов (по 9.128)
Fц = Fδ + FZ1 + FZ2 + Fa + Fj = 726,5 + 87,8 + 91,1 + 147 + 11,3 = 1063,7 А.
42. Коэффициент насыщения магнитной цепи по (9.129)
kμ = FЦ/ Fδ = 1063,7/726,5 = 1,46.
43. Намагничивающий ток по (9.130)
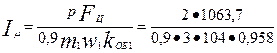 =7,91 A.
=7,91 A.
Относительное значение по (9.131)
Iμ* = Iμ /I1НОМ = 7,91/29,3 = 0,27.
0,2 < Iμ* < 0,3.
Параметры рабочего режима
44. Активное сопротивление обмотки статора по (9.132)
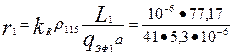 =0,355 Ом
=0,355 Ом
(дня класса нагревостойкости изоляции F расчетная температура vрасч = 115° С; для медных проводников ρ115 = 10-6/41 Ом  м).
м).
Длина проводников фазы обмотки по (9.134)
L1 = lcp1 w1 = 0,742 • 104 = 77,17 м;
по (9.135) lср1 = 2(lП1 + lл1) = 2(0,14 + 0,231) = 0,742 м; lП1 = l1 = 0,14 м; по (9.136)
lл1 = Клbкт + 2В = 1,3 • 0,162 + 2 • 0,01 = 0,231 м, где В = 0,01 м; по табл. 9.23 Кл = 1,3;
по (9.138)
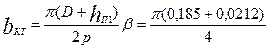 =0,162 м
=0,162 м
Длина вылета лобовой части катушки по (9.140)
lвыл = kВЫЛВКТ + В = 0,4 • 0,162 + 0,01 = 0,0748 м = 74,8 мм, где по табл. 9.23 Квыл = 0,4.
Относительное значение r1
r1* = r1 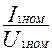 =0,355
=0,355 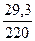 = 0,047.
= 0,047.
45. Активное сопротивление фазы алюминиевой обмотки ротора по (9.168)
r2 =rс + 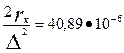 =40,89
=40,89  10-6 +
10-6 + 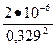 = 59,37
= 59,37  10-6 Ом;
10-6 Ом;
по (9.169)
rc = ρ115 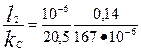 = 40,89
= 40,89  10-6 Ом;
10-6 Ом;
здесь kr = 1 ;
по (9.170)
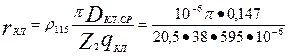 = 10-6 Ом,
= 10-6 Ом,
где для литой алюминиевой обмотки ротора ρ115 = 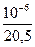 Ом
Ом  м
м
Приводим r2 к числу витков обмотки статора по (9.172), (9.173):
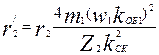 = 59,37
= 59,37  10-6
10-6 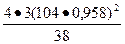 = 0,186 Ом,
= 0,186 Ом,
здесь kc1 = 1.
Относительное значение
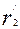 = r2
= r2 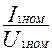 =0,186
=0,186 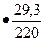 =0,0248
=0,0248
46. Индуктивное сопротивление фазы обмотки статора по (9.152)
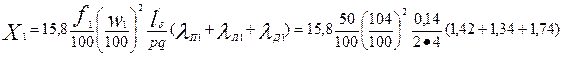 =673 Ом,
=673 Ом,
где по табл. 9.26 (см. рис. 9.50, е) и по рис. 9.73
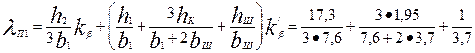 =1,42
=1,42
где (см. рис. 9.50, е и 9.73)
h2 = hП.К – 2bИЗ = 18,1 - 2 • 0,4 = 17,3 мм; b1 = 7,6 мм; hк = 0,5(b1 - bш) = 0,5(7,6 - 3,7) = 1,95 мм; h1 = 0 (проводники закреплены пазовой крышкой); kβ = 1; k'β = 1; l'δ = lδ = 0,14м по (9.154);
по (9.159)
λл1 =0,34 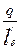 (lл1 - 0,64βτ) = 0,34
(lл1 - 0,64βτ) = 0,34 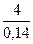 (0,231- 0,64
(0,231- 0,64  0,145) = 1,34;
0,145) = 1,34;
по (9.174)
λд1 = 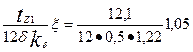 =1,74
=1,74
по (9.176)
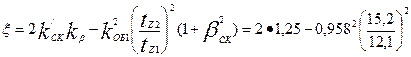 =1,05
=1,05
для βcк = 0 и tz2/tz1 = 15,2/12,1 = 1,26 по рис. 9.51, д k'CK = 1,25.
Относительное значение
x1* = x1 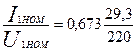 = 0,09
= 0,09
47. Индуктивное сопротивление фазы обмотки ротора по (9.177)
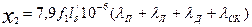 = 7,9•50•0,14(2,58+0,59+2,09) = 291•10-6 Ом,
= 7,9•50•0,14(2,58+0,59+2,09) = 291•10-6 Ом,
где по табл. 9.27 (см. рис. 9.52, а, ж)
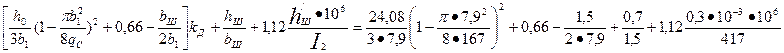 = 2,58
= 2,58
где (см. рис. 9.52, а, ж и рис. 9.73)
h0 = h1 + 0,4b2 = 22,4 + 0,4 • 4,2 = 24,08 мм; b1 = 7,9 мм; bш = 1,5 мм;
hш = 0,7 мм; h'ш = 0,3 мм; qc = 167 мм2; по (9.178)
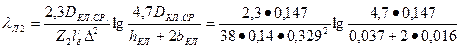 =0,587
=0,587
по (9. 180)
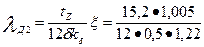 =2,09
=2,09
по (9.181)
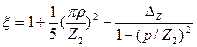 =1,005
=1,005
так как при закрытых пазах Δz ≈ 0.
Приводим Х2 к числу витков статора по (9.172) и (9.183):
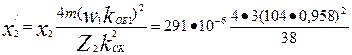 = 0,912 Ом.
= 0,912 Ом.
Относительное значение
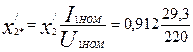 = 0,121
= 0,121
Расчет потерь
48. Потери в стали основные по (9.187)
Рст.осн = р1,0/50 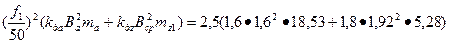 = 276,4 Вт
= 276,4 Вт
[p1,0/5,0 = 2,5 Вт/кг для стали 2013 по табл. 9.28];
по (9.188)
ma = π(Dа – ha) ha lст1 kc1 vc = π(0,272 – 0,0223) • 0,0223 • 0,14 • 0,97 • 7,8 • 103 = 18,53 кг;
по (9.189)
mz1 = hz1 bz1cp Z1 lст1 kc1 vc1 = 21,2 • 10-3 • 4,9 • 10-3 • 48 • 0,14 • 0,97 • 7,8 – 10-3 = 5,28 кг;
kДА = 1,6; kдz= 1,8 (см. § 9.11)].
49. Поверхностные потери в роторе по (9.194)
Рпов2 =pпов2(tz2 - bш2)Z2 lcт2 = 242,4(15,2 – 1,5)38,0,14 = 17,7 Вт;
по (9.192)
Рпов2 = 0,5 k02 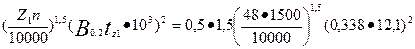 = 242,4 Вт/м2.
= 242,4 Вт/м2.
где k02 = 1,5;
по (9.190)
B01(2) = β01(2) kδ Bδ = 0,37 • 1,22 • 0,749 = 0,338 Тл;
где bш/δ = 3,7/0,5 = 7,4 по рис. 9.53 β02 = 0,37.
50. Пульсационные потери в зубцах ротора по (9.200)
Pпул2 ≈ 0,11 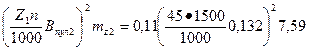 = 75,4 Вт
= 75,4 Вт
по (9.196)
Впул2 = 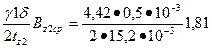 = 0,132 Тл
= 0,132 Тл
Bz2ср = 1,81 Тл из п. 37 расчета; γ1 = 4,42 из п. 35 расчета;
по (9.201)
mz2 = Z2 hz2 bz2ср lст2 kc2 = 38 • 29 • 10-3 • 6,5 • 10-3 • 0,14 • 0,97 • 7800 = 7,59 кг;
hz2 = 29 мм из п. 37 расчета; bz2 = 6,5 мм из п. 32 расчета.
51. Сумма добавочных потерь в стали по (9.202)
Рст.доб = Рпов1 + Рпул1 + Рпов2 + Рпул2= I7,7 + 75,4 = 93,1 Вт
(Рпов1 и Рпул1 ≈ 0, см. § 9.11).
52. Полные потери в стали по (9.203)
Pст = Рст.осн + Рст.доб = 276,4 + 93,1 = 369,5 Вт
53. Механические потери по (9.210)
Рмех = Кт ( n /10)2 D 4 a = 0,95 (1500/10)2 0,2724 = 117Вт
[для двигателей с 2р = 4 коэффициент Кт = 1,3(1 - Da) = 1,3(1 - 0,272) = 0,95].
54. Холостой ход двигателя:
по (9.217)
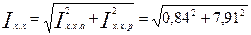 = 7,95 А
= 7,95 А
[по (9.128)
I х.х.а = 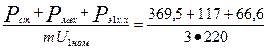 = 0,84 А
= 0,84 А
где по (9.219)
Рэ1х.х ≈ 3 I2μ r1 = 3  7,912
7,912  0,355 = 66,6 Вт];
0,355 = 66,6 Вт];
по (9.221)
cos φх.х = Iх.х.а / Iх.х = 0,84/7,95 = 0,11
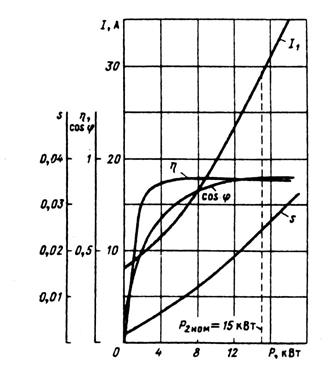
Рис 9.74. Рабочие характеристики спроектированного
двигателя с короткозамкнутым ротором (Р2ном=15 кВт,
2р = 4, Uном=220/380В, Iн=28,4 А,
соs φном = 0,894; ηном = 0,892, Sном = 0,024)
Расчет рабочих характеристик
55. Параметры
по (9.184)
r12 = 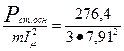 = 1,47 Ом;
= 1,47 Ом;
по (9.185)
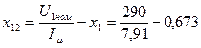 = 27,14 Ом;
= 27,14 Ом;
по (9.223)
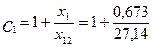 = 1,025
= 1,025
используем приближенную формулу, так как |у | < 1°:
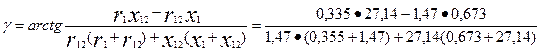 = arctg 0,01 рад = |34'| < 1º
= arctg 0,01 рад = |34'| < 1º
Активная составляющая тока синхронного холостого хода: по (9.226)
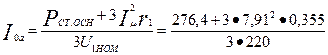 = 0,52 A
= 0,52 A
по (9.227)
а' = 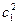 = 1,0252 = 1,051; b' = 0;
= 1,0252 = 1,051; b' = 0;
а = с1 r1 = 1,025 • 0,355 = 0,364 Ом;
b = c1(x1 + с1 x'2) = 1,025(0,673 + 1,025•0,912) = 1,648 Ом.
Потери, не изменяющиеся при изменении скольжения,
Рст + Рмех = 369,5 + 117 = 487 ≈ 0,49 кВт.
56. Рассчитываем рабочие характеристики для скольжений s = 0,005; 0,01; 0,015; 0,02; 0,025; 0,03, принимая предварительно, что sном ≈ 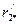 = 0,025. Результаты расчета сведены в табл. 9.36. После построения рабочих характеристик (рис. 9.74) уточняем значение номинального скольжения: sном = 0,024.
= 0,025. Результаты расчета сведены в табл. 9.36. После построения рабочих характеристик (рис. 9.74) уточняем значение номинального скольжения: sном = 0,024.
Расчет рабочих характеристик см. § 9.12.
Номинальные данные спроектированного двигателя:
Р2ном = 15 кВт, U1ном = 220/380 В, I1ном = 28,4 А, соs φном = 0,894, ηном = 0,892.
Таблица 9.36. Рабочие характеристики асинхронного двигателя (см. табл. 9.30)
Рном = 15 кВт; 2р = 4; U1ном = 220/380 В; I0a =0,52 А;
I0р ≈ Iμ = 7,91 А; Рст + Ртр.щ. + Рмех = 0,49 кВт;
r1 = 0,355 Ом; r/2 = 0,186 Ом; с1 = 1,025;
a/ = 1,051; a = 0,364 Ом; b/ = 0 Ом; b = 1,65 Ом
| № п/п |
Расчетная формула | Раз-мерность | Скольжение s | ||||||
| 0,005 | 0,01 | 0,015 | 0,02 | 0,025 | 0,03 | Sном = =0,024 | |||
| 1 | 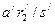
| Ом | 39,1 | 19,55 | 13,03 | 9,77 | 7,82 | 6,52 | 8,15 |
| 2 | 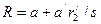
| Ом | 39,46 | 19,91 | 13,39 | 10,13 | 8,81 | 6,88 | 8,51 |
| 3 | Х = b + 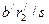
| Ом | 1,65 | 1,65 | 1,65 | 1,65 | 1,65 | 1,65 | 1,65 |
| 4 | 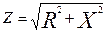
| Ом | 39,49 | 19,98 | 13,49 | 10,26 | 8,34 | 7,08 | 8,67 |
| 5 | 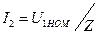
| А | 5,57 | 11,011 | 16,31 | 21,44 | 26,38 | 31,07 | 25,37 |
| 6 | 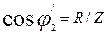
| - | 6,999 | 0,996 | 0,993 | 0,987 | 0,981 | 0,972 | 0,982 |
| 7 | 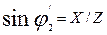
| - | 0,042 | 0,083 | 0,122 | 0,161 | 0,198 | 0,233 | 0,19 |
| 8 | 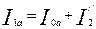 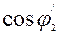
| А | 6,08 | 11,49 | 16,72 | 21,68 | 26,4 | 30,72 | 25,43 |
| 9 | 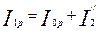 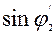
| А | 8,14 | 8,82 | 9,9 | 11,36 | 13,13 | 15,15 | 12,73 |
| 10 | 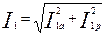
| А | 10,16 | 14,48 | 19,43 | 24,28 | 29,48 | 34,25 | 28,44 |
| 11 | 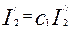
| А | 5,71 | 11,29 | 16,72 | 21,98 | 27,04 | 31,85 | 26 |
| 12 | P1 = 3 U1ном I1a 10 -3 | кВт | 4,01 | 7,58 | 11,03 | 14,31 | 17,42 | 20,28 | 16,78 |
| 13 | Рэ1 = 3 I12 r1 10 -3 | кВт | 0,11 | 0,223 | 0,402 | 0,638 | 0,926 | 1,25 | 0,861 |
| 14 | Рэ2 = 3 (I11) 2 r/2 10 -3 | кВт | 0,018 | 0,071 | 0,156 | 0,27 | 0,408 | 0,566 | 0,377 |
| 15 | Рдоб = 0,005 Р1 | кВт | 0,034 | 0,048 | 0,064 | 0,081 | 0,097 | 0,113 | 0,084 |
| 16 | Σ Р = Рст + Рмех + Ртр.щ + Рэ1+ +Рэ2 + Рэ.щ + Рдоб | кВт | 0,652 | 0,832 | 1,112 | 1,479 | 1,921 | 2,418 | 1,812 |
| 17 | Р2 = Р1 - ∑Р | кВт | 3,36 | 6,75 | 9,92 | 12,83 | 15,5 | 17,86 | 14,97 |
| 18 | η = 1 - ∑Р/ P1 | - | 0,838 | 0,891 | 0,899 | 0,897 | 0,89 | 0,881 | 0,892 |
| 19 | cos φ = I1a/I1 | - | 0,598 | 0,794 | 0,861 | 0,886 | 0,896 | 0,897 | 0,894 |
Расчет пусковых характеристик
а) Расчет токов с учетом влияния изменения параметров под влиянием эффекта вытеснения тока (без учета влияния насыщения от полей рассеяния)
Расчет проводится по формулам табл. 9.32 в целях определения токов в пусковых режимах для дальнейшего учета влияния насыщения на пусковые характеристики двигателя. При отсутствии необходимости учитывать влияние насыщения от полей рассеяния расчет пусковых характеристик проводится аналогично, включая последние пункты формуляра (см. табл. 9.32). Подробный расчет приведен для s = 1. Данные расчета остальных точек сведены в табл. 9.37.
Таблица 9.37. Расчет токов в пусковом режиме асинхронного двигателя
с короткозамкнутым ротором с учетом влияния эффекта вытеснения тока
(см. табл. 9. 32)
Р2ном = 15 кВт; U1ном = 220/380 В; 2р = 4; I1ном = 28,4 А;
I'2ном = 26 A; x1 = 0,673 Ом; x'2 = 0,912 Ом; х12п = 39,62 Ом;
с1п = 1,017; r1 = 0,355 Ом; r'2 = 0,186 Ом; sном = 0,024
| № п/п | Расчетная формула | Раз-мерность | Скольжение s | |||||
| 1 | 0,8 | 0,5 | 0,2 | 0,1 | Sкр = =0,14 | |||
| 1 | ξ = 6361 hc 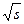 (9.245) (9.245)
| - | 1,81 | 1,63 | 1,28 | 0,81 | 0,57 | - |
| 2 |
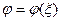
| - | 0,66 | 0,45 | 0,19 | 0,04 | 0,01 | - |
| 3 | 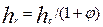
| мм | 17,2 | 19,7 | 23,9 | 28,5 | 28,5 | 28,5 |
| 4 | 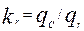
| - | 1,46 | 1,3 | 1,12 | 1 | 1 | 1 |
| 5 | 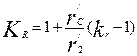
| - | 1,32 | 1,21 | 1,08 | 1 | 1 | 1 |
| 6 | 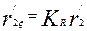
| Ом | 0,246 | 0,225 | 0,2 | 0,186 | 0,186 | 0,186 |
| 7 | 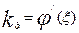
| - | 0,81 | 0,86 | 0,93 | 0,97 | 0,99 | 0,98 |
| 8 | 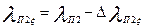
| - | 2,33 | 2,4 | 2,49 | 2,54 | 2,57 | 2,55 |
| 9 | 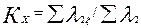
| - | 0,95 | 0,97 | 0,98 | 0,99 | 1 | 1 |
| 10 | 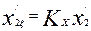
| Ом | 0,866 | 0,885 | 0,894 | 0,903 | 0,912 | 0,908 |
| 11 | 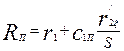
| Ом | 0,605 | 0,641 | 0,762 | 1,3 | 2,25 | 1,7 |
| 12 | 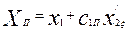
| Ом | 1,55 | 1,57 | 1,58 | 1,59 | 1,6 | 1,6 |
| 13 | 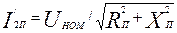
| А | 132,2 | 129,7 | 125,4 | 107,1 | 79,7 | 94,2 |
| 14 | 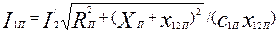
| А | 135,1 | 132,6 | 128,2 | 109,6 | 81,7 | 96,8 |
57. Активное сопротивление обмотки ротора с учетом влияния эффекта вытеснения тока [vрасч = 115° С, p115 = 10-6/20,5 Ом  м; bс/ bп = l; f1 = 50 Гц];
м; bс/ bп = l; f1 = 50 Гц];
по рис. 9.73 hc = hп - (hш + h'ш) = 29,5 - (0,7 + 0,3) = 28,5 мм;
ξ = 2πhс 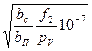 = 63,61 hc
= 63,61 hc 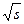 = 63,61
= 63,61  0,0285 = l,81;
0,0285 = l,81;
по рис. 9.57 для ξ = 1,81; = 1,81 находим φ = 0,66;
по (9.246)
hr = hc / (1+φ) = 0,0285/(1+0,66) = 0,1772 м = 17,2 мм;
по (9.253), так как (0,5 • 7,9) < 17,2 < (22,4 + 0,5 • 7,9) (см. рис. 9.73)
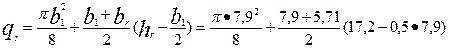 = 114,7 мм2,
= 114,7 мм2,
где
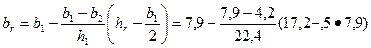 = 5,71 мм;
= 5,71 мм;
по (9.247)
kr = qс/qr = 167/114,7 =1,46
(qc - по п. 33 расчета);
по (9.257)
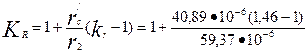 = 1,32
= 1,32
(по п. 45 расчета r'c = rс = 40,89•10-6 Ом; r2 = 59,37•10-6 Ом). Приведенное сопротивление ротора с учетом влияния эффекта вытеснения тока
r'2ξ = Кr r'2 = 1,32 • 0,186 = 0,246 Ом.
58. Индуктивное сопротивление обмотки ротора с учетом влияния эффекта вытеснения тока по рис. 9.58 для ξ = 1,81 (см. п. 57 расчета) φ' = kд = 0,81; по табл. 9.27, рис. 9.52, а, ж (см. также п. 47 расчета) и по (9.262)
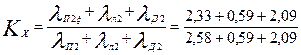 = 0,59
= 0,59
где
по п. 47 расчета λп2ξ = λп2 – Δ λп2ξ = 2,58 - 0,25 = 2,33,
Δ λп2ξ = λ'п2 (1 - kд) = 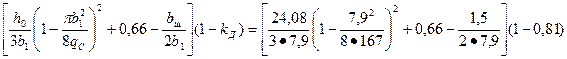 =
=
= 0,25
по (9.261) — см. также п. 47 расчета
х'2ξ = х'2 Кх = 0,912 • 0,95 = 0,866 Ом.
59. Пусковые параметры по (9.277) и (9.278)
х12п = kμ x12 = 1,46 • 27,14 = 39,62 Ом;
c12п = 1 + 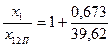 = 1,017
= 1,017
60. Расчет токов с учетом влияния эффекта вытеснения тока:
по (9.280) для s =1
Rп = r1 + c1п r'2ξ/s = 0,355 + 1,017 • 0,246 = 0,605 Ом;
Хп = х1 + c1п x'2ξ = 0,673 + 1,017 • 0,866 = 1,55 Ом;
по (9.281)
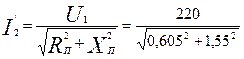 = 132,2 А;
= 132,2 А;
по (9.283)
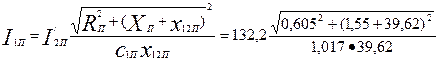 = 135,1 А.
= 135,1 А.
Расчет пусковых характеристик с учетом влияния вытеснения тока и насыщения от полей рассеяния
Расчет проводим для точек характеристик, соответствующих s = 1; 0,8; 0,5; 0,1, при этом используем значения токов и сопротивлений для тех же скольжений с учетом влияния вытеснения тока (см. табл. 9.37).
Данные расчета сведены в табл. 9.38. Подробный расчет приведен для s = 1.
Таблица 9.38. Расчет пусковых характеристик асинхронного двигателя
с короткозамкнутым ротором с учетом эффекта вытеснения тока
и насыщения от полей рассеяния (см. табл. 9.33)
Р2ном = 15 кВт; U1 = 220/380 В; 2р = 4; I1ном = 28,4 A; I'2ном = 26 А;
х1 = 0,67 Ом; х'2 = 0,912 Ом; х12п = 39,62 Ом; r1 = 0,355 Ом;
r'2 =0,186 Ом; sном = 0,024; СN = 0,978
| № п/п
| Расчетная формула
| Раз-мерность
|
Скольжение s | |||||
| 1 | 0,8 | 0,5 | 0,2 | 0,1 | sкр= = 0,14 | |||
| 1 | kнас | — | 1,35 | 1,3 | 1,2 | 1,1 | 1,05 | 1,08 |
| 2 | Fп.ср = 0,7 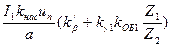
| А | 3668 | 3467 | 3094 | 2422 | 1725 | 2102 |
| 3 | ВФδ = Fп.ср 10-6 / (1,6 δ CN) | Тл | 4,69 | 4,43 | 3,95 | 3,1 | 2,21 | 2,69 |
| 4 | kδ = f (ВФδ) | — | 0,5 | 0,53 | 0,61 | 0,72 | 0,84 | 0,79 |
| 5 | c1 = (tz1 - bш)(1 - kδ) | мм | 4,2 | 3,95 | 3,28 | 2,35 | 1,34 | 1,76 |
| 6 | λп1нас = λп1 - Δ λп1нас | — | 1,17 | 1,18 | 1,2 | 1,25 | 1,31 | 1,28 |
| 7 | λД1 = kδ λД1 | — | 0,87 | 0,92 | 1,06 | 1,25 | 1,46 | 1,37 |
| 8 | х1нас = х1 ∑ λ1нас / ∑ λ1 | Ом | 0,505 | 0,514 | 0,538 | 0,574 | 0,615 | 0,597 |
| 9 | с1п = 1 + х1нас / х12п | — | 1,013 | 1,013 | 1,014 | 1,014 | 1,016 | 1,015 |
| 10 | с2 =(tz2 – bш2)(1 - kδ) | мм | 6,85 | 6,44 | 5,34 | 3,84 | 2,19 | 2,88 |
| 11 | λп2ξнас = λп2ξ - Δλп2нас | — | 1,78 | 1,86 | 1,96 | 2,06 | 2,17 | 2,11 |
| 12 | λД2 = kδ λД2 | — | 1,05 | 1,11 | 1,27 | 1,5 | 1,76 | 1,65 |
| 13 | х'2ξнас = х'2 ∑ λ2ξнас / ∑ λ2 | Ом | 0,593 | 0,617 | 0,662 | 0,72 | 0,787 | 0,754 |
| 14 | Rп.нас = r1 + c1п.нас r'2ξ / s | Ом | 0,6 | 0,64 | 0,76 | 1,3 | 2,24 | 1,7 |
| 15 | Хп.нас = х1нас + с1п.нас х'2ξнас | Ом | 1,11 | 1,14 | 1,21 | 1,3 | 1,41 | 1,36 |
| 16 | I'2нас = U1 / 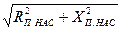
| А | 174,4 | 168,3 | 153,9 | 119,7 | 83,1 | 101,1 |
| 17 | I1нас = I'2нас 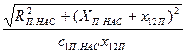
| А | 177 | 170,9 | 156,4 | 122 | 84,6 | 103,1 |
| 18 | k'нас = I1нас / I1п (сравнить с принятым в п.1 kнас) | — | 1,31 | 1,29 | 1,22 | 1,11 | 1,04 | 1,07 |
| 19 | I1* = I1нас / I1ном | — | 6,2 | 6 | 5,5 | 4,3 | 3 | 3,6 |
| 20 | М* = 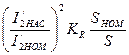
| — | 1,43 | 1,52 | 1,82 | 2,54 | 2,45 | 2,59 |
61. Индуктивные сопротивления обмоток. Принимаем kнас = 1,35:
по (9.263)
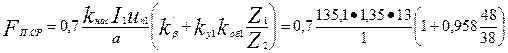 = 3668 А
= 3668 А
по (9.265)
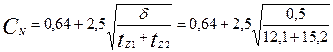 = 0,968;
= 0,968;
по (9.264)
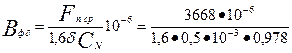 = 4,69 Тл
= 4,69 Тл
Пo рис. 9.61 для ВФδ = 4,69 Тл находим kδ = 0,5.
Коэффициент магнитной проводимости пазового рассеяния обмотки статора с учетом влияния насыщения:
по (9.266)
сЭ1 = (tz1 – bш1)(1 – kδ) = (12,1 – 3,7)(1 – 0,5) = 4,2;
по (9.269)
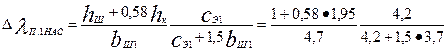 = 0,25
= 0,25
[hк = 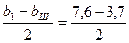 = 1,95мм (см. рис. 9.73)];
= 1,95мм (см. рис. 9.73)];
по (9.272)
λп1нас = λп - Δλп1нас = 1,42 - 0,25 = 1,18.
Коэффициент магнитной проводимости дифференциального рассеяния обмотки статора с учетом влияния насыщения по (9.274)
λД1нас = λД1 кδ =1,74 • 0,5 = 0,87.
Индуктивное сопротивление фазы обмотки статора с учетом влияния насыщения по (9.275)
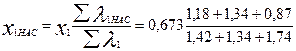 = 0,505 Ом
= 0,505 Ом
Коэффициент магнитной проводимости пазового рассеяния обмотки ротора с учетом влияния насыщения и вытеснения тока:
по (9.271) (см. п. 47 и 58 расчета)
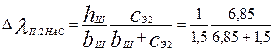 = 0,55
= 0,55
где по (9.270)
сЭ2 = (t2 - bш )(1 - kδ) = (15,2 - 1,5)(1 - 0,5) = 6,85
(для закрытых пазов ротора hш2 = h'ш + hш = 0,3 + 0,7 = 1 мм);
по (9.273)
λп2нас = λп2ξ - Δλп2нас = 2,33 - 0,55 = 1,78.
Коэффициент магнитной проводимости дифференциального рассеяния ротора с учетом влияния насыщения по (9.274)
λД2нас = λД2 кδ = 2,09 • 0,5 = 1,05.
Приведенное индуктивное сопротивление фазы обмотки ротора с учетом влияния эффекта вытеснения тока и насыщения по (9.276)
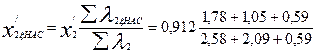 = 0,593 Ом;
= 0,593 Ом;
по (9.278)
с1П = 1 + 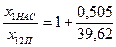 = 1,013
= 1,013
здесь х12п по (9.277).
62. Расчет токов и моментов:
по (9.280)
Rп.нас = r1 + c1п.нас 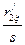 = 0,355 + 1,013 • 0,246 = 0,604 Ом;
= 0,355 + 1,013 • 0,246 = 0,604 Ом;
Хп.нас = Х1нас + с1п.нас х'2ξнас = 0,505 + 1,013.0,593 = 1,11 Ом;
по (9.281)
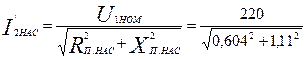 = 174,1 А
= 174,1 А
по (9.283)
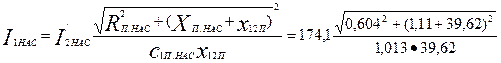 = 176,7 А;
= 176,7 А;
Кратность пускового тока с учетом влияния эффекта вытеснения тока и насыщения
Iп* = 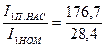 = 6,2
= 6,2
Кратность пускового момента с учетом влияния вытеснения тока и насыщения по (9.284)
Мп* = 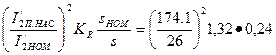 = 1,43
= 1,43
Полученный в расчете коэффициент насыщения
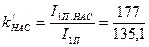 = 1,31
= 1,31
отличается от принятого kнас =1,35 менее чем на 3 %.
Для расчета других точек характеристики задаемся kнас, уменьшенным в зависимости от тока I1 (см. табл. 9.37);
принимаем при
s = 0,8 kнас = 1,3;
s = 0,5 kнас = 1,2;
s = 0,2 kнас = 1,1;
s = 0,1 kнас = 1,05.
Данные расчета сведены в табл. 9.38, а пусковые характеристики представлены на рис. 9.75.
63. Критическое скольжение определяем после расчета всех точек пусковых характеристик (табл. 9.38) по средним значениям сопротивлений x1нас и х'2ξнас, соответствующим скольжениям s = 0,2... 0,1:
по (9.286)
SКР = 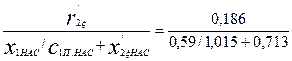 = 0,14,
= 0,14,
после чего рассчитываем кратность максимального момента: М*max = 2,59 (см. табл. 9.38).
Спроектированный асинхронный двигатель удовлетворяет требованиям ГОСТ как по энергетическим показателям (КПД и сos φ), так и по пусковым характеристикам.
Тепловой расчет
64. Превышение температуры внутренней поверхности сердечника статора над температурой воздуха внутри двигателя по (9.315)
Δυпов1 = К 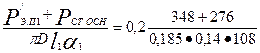 = 44,62 ºС
= 44,62 ºС
[по табл. 9.35 К = 0,2; по (9.313) Р'э.п = kp Pэ1 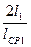 =1,07•861•2•0,14/0,742 = 348 Вт, где из табл. 9.36 для s = sном находим Рэ1 = 861 Вт; по рис. 9.67, б а1 = 108 Вт/м2 ºС; kp = 1,07]
=1,07•861•2•0,14/0,742 = 348 Вт, где из табл. 9.36 для s = sном находим Рэ1 = 861 Вт; по рис. 9.67, б а1 = 108 Вт/м2 ºС; kp = 1,07]
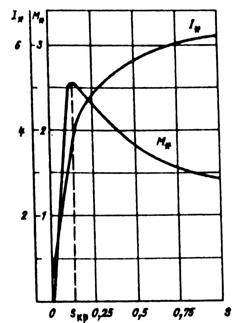
Рис. 9.75. Пусковые характеристики спроектированного
двигателя с короткозамкнутымротором
(Р2 = 15 кВт, 2р=4, Uном = 220/380 В, Мп* = 1,43, Iп* = 6,2, Мmax = 2,59)
65. Перепад температуры в изоляции пазовой части обмотки статора по (9.316)
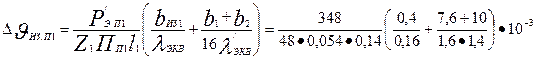 = 3,15 ºС
= 3,15 ºС
[по (9.317) Пп1 = 2hпк + b1 + b2 = 2 • 18,3 + 10 + 7,6 = 54,2 мм = 0,054 м; для изоляции класса нагревостойкости Fλэкв = 0,16 Вт/м2, по рис. 9.69 для d/dиз = 1,5/1,585 = 0,95 находим λ'экв = 1,4 Вт/(м2  °С)].
°С)].








