Коэффициент магнитной проводимости лобового рассеяния
λл = 0,34 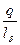 ( l л – 0,64 β τ ) (9.159)
( l л – 0,64 β τ ) (9.159)
где q и lл — число пазов на полюс и фазу и длина лобовой части витка обмотки; β = урасч / τ — укорочение шага обмотки, для которой проводится расчет, т. е. обмотки статора или фазного ротора.
Коэффициент магнитной проводимости дифференциального рассеяния для обмоток статора и фазного ротора
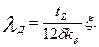 (9.160)
(9.160)
Значение коэффициента ξ зависит от числа q, укорочения шага обмотки и размерных соотношений зубцовых зон и воздушного зазора.
Ниже приводятся формулы, в которые при расчете ξ, для обмоток статора или ротора следует подставлять данные обмоток и зубцовых зон соответственно статора или ротора.
Для обмоток статора и ротора при q, выраженном целым числом (q ≥ 2), для обмотки с β = 1
ξ = 2 + 0,022 q 2 – k 2 об (1 + Δ z ); (9.161)
при укороченном шаге обмотки (β < 1)
ξ = k '' q 2 + k ' β – k 2 об (1 + Δ z ); (9.162)
при дробном (q ≥ 2)
ξ = k''q2 + 2k''β – k2 об ( 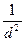 + Δ z); (9.163)
+ Δ z); (9.163)
при дробном q, значение которого 1 < q < 2,
ξ = k '' q 2 + 2 k '' β – 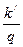 – k 2 об (
– k 2 об ( 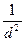 + Δ z ); (9.164)
+ Δ z ); (9.164)
В этих формулах коэффициенты Δz, k', k" и k"β определяют по кривым, приведенным на рис. 9.51. Для определения k"β и k' необходимо найти дробную часть числа q, равную c/d (дробное число q = b + c/d, где b — целое число, c/d < 1 — дробная часть числа q), коэффициент k'β — по (9.156) или (9.157).
Индуктивное сопротивление обмотки фазного ротора, определенное по (9.152), должно быть приведено к числу витков обмотки статора:
х'2 = v 12 x 2, (9.165)
где v12 — коэффициент приведения сопротивлений по (9.151).
9.10.3. Сопротивления обмоток двигателей с короткозамкнутыми роторами
Активное сопротивление фазы обмотки статора двигателя с короткозамкнутым ротором рассчитывается так же, как и для двигателя с фазным ротором.
Активное сопротивление фазы короткозамкнутого ротора определяется следующим образом. Как говорилось выше, за фазу обмотки, выполненной в виде беличьей клетки, принимают один стержень и два участка замыкающих колец (см. рис. 9,35). Токи в стержнях и замыкающих кольцах различны, поэтому их сопротивления при расчете общего сопротивления фазы должны быть приведены к одному току. Таким образом, сопротивление фазы короткозамкнутого ротора r2 является расчетным параметром, полученным из условия равенства электрических
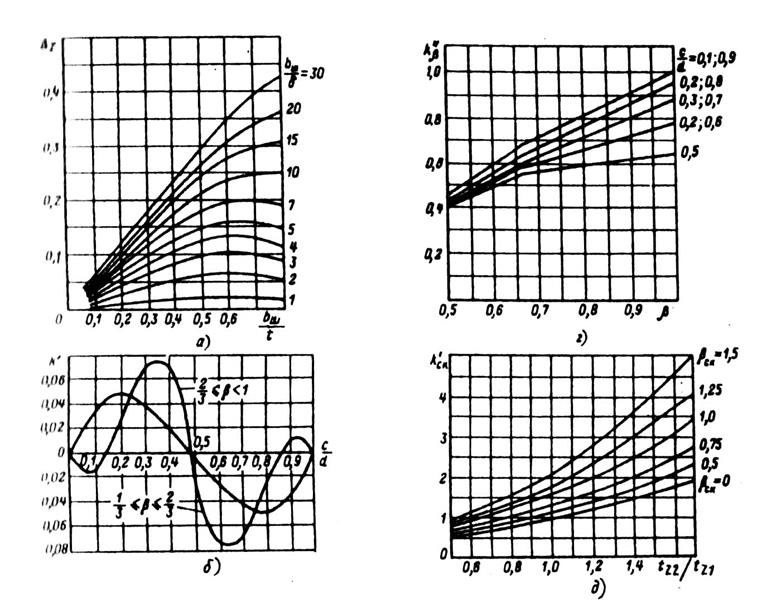
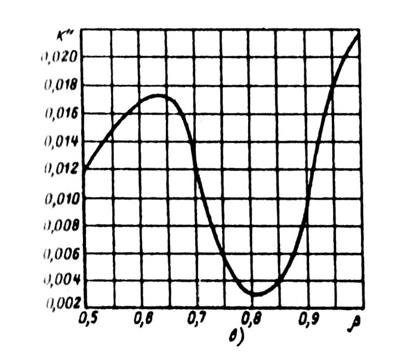
Рис. 9.51. Коэффициенты к расчету проводимости
дифференциального рассеяния:
а — коэффициент Δz в зависимости от размерных соотношений bш/tz и bш/S;
б — коэффициент k' в зависимости от дробной части числа q;
в — коэффициент К' в зависимости от укорочения шага обмотки β;
г — коэффициент К''β в зависимости от укорочения шага обмотки β и дробной части числа q;
д — коэффициент k'ск в зависимости от соотношения tz2/tz1 и относительного скоса пазов βck
потерь в сопротивлении r2 от тока I2 и суммарных потерь в стержне и участках замыкающих колец соответственно от тока в стержне Ic и тока в замыкающем кольце Iкл реальной машины:
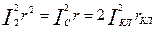 (9.166)
(9.166)
где Iс — ток в стержне ротора; Iкл — ток в замыкающих кольцах; rC — сопротивление стержня; rкл — сопротивление участка замыкающего кольца, заключенного между двумя соседними стержнями (см. рис. 9.35).
Ток Iс называют током ротора и в расчетах обозначают I2.
Учитывая, что
I кл = I с / Δ = I2 / Δ, (9.167)
где Δ = 2sin 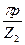 — (см. § 9.7), из (9.167), получаем
— (см. § 9.7), из (9.167), получаем
r 2 = r с + 2 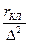 (9.168)
(9.168)
где
rc = 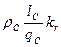 ; (9.169)
; (9.169)
r кл = 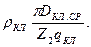 (9.170)
(9.170)
В этих выражениях Iс — полная длина стержня, равная расстоянию между замыкающими кольцами, м; Dкл.ср — средний диаметр замыкающих колец, м (см. рис. 9.37):
D кл .ср = D2 - h кл; (9.171)
qc — сечение стержня, м2; kr — коэффициент увеличения активного сопротивления стержня от действия эффекта вытеснения тока; при расчете рабочих режимов в пределах изменения скольжения от холостого хода до номинального для всех роторов принимают kr = 1; qкл — площадь поперечного сечения замыкающего кольца, м2; рс и ркл — соответственно удельные сопротивления материала стержня и замыкающих колец, Ом  м, при расчетной температуре (см. табл. 5.1).
м, при расчетной температуре (см. табл. 5.1).
Сопротивление r2 для дальнейших расчетов должно быть приведено к числу витков первичной обмотки. Выражение коэффициента приведения для сопротивления фазы короткозамкнутого ротора получают, подставляя в (9.151) значения m2 = Z2, w 2 = 1/2, kоб2 = 1 и учитывая влияние скоса пазов:
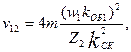 (9.172)
(9.172)
где коэффициент скоса пазов (по 3.17)
k ск = 2 sin 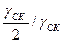 ;
; 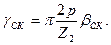
Обычно значения βск выражают в долях зубцового деления ротора tz2. При скосе пазов ротора на одно зубцовое деление статора γck = π2p / Z1. В этом случае в двигателях с 2р = 2 из-за малости угла γck принимают kcк = 1.
Приведенное значение активного сопротивления фазы обмотки короткозамкнутого ротора
r ' 2 = r2 v 12. (9.173)
Индуктивное сопротивление рассеяния обмотки статора асинхронного двигателя с короткозамкнутым ротором рассчитывается по той же формуле, что и для статора с фазными роторами, т. е.
x = 1,58 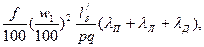 (9.174)
(9.174)
Входящий в формулу коэффициент магнитной проводимости пазового рассеяния λп определяют в зависимости от конфигурации пазов по формулам табл. 9.26.
Коэффициент магнитной проводимости лобового рассеяния λл определяется по (9.159).
Коэффициент магнитной проводимости дифференциального рассеяния λд1 определяют по формуле
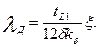 (9.174а)
(9.174а)
в которой ξ, находят следующим образом.
При открытых пазах статора и отсутствии скоса статора или ротора
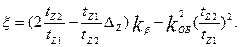 (9.175)
(9.175)
При полузакрытых или полуоткрытых пазах статора с учетом скоса пазов
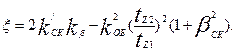 (9.176)
(9.176)
В этих формулах tz1 и tz2 — зубцовые деления статора и ротора; ΔZ определяют по кривой рис. 9.51, a, kβ определяют по (9.155) или (9.158); βcк = βcк/tz2 — скос пазов, выраженный в долях зубцового деления ротора. При отсутствии скоса пазов bск = 0; k'cк определяют по кривым рис. 9.51, д в зависимости от tz2/tz1 и βcк (при отсутствии скоса пазов — по кривой, соответствующей βск = 0).
Индуктивное сопротивление обмотки короткозамкнутого ротора определяют по формуле
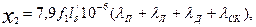 (9.177)
(9.177)
полученной после подстановки в (9.152) значений m2 = Z2 и q2 = 1/(2р) обмотки короткозамкнутого ротора и введения дополнительного слагаемого λск.
Коэффициент магнитной проводимости пазового рассеяния обмотки короткозамкнутого ротора рассчитывают по приведенным в табл. 9.27 формулам в зависимости от конфигурации паза ротора (рис. 9.52).
Таблица 9.27. Расчетные формулы для определения коэффициентов
магнитной проводимости пазового рассеяния короткозамкнутых роторов
| Рисунок | Расчетные формулы |
| 9.52, а | 
|
| 9.52,6 | 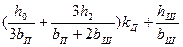
|
| 9.52, в | 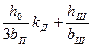
|
| 9.52, г | 
|
| 9.52, д | 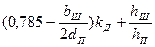
|
При расчете номинального режима двигателя во всех формулах kд= 1.
При закрытых пазах ротора любой конфигурации (рис. 9.52, а—д) в расчетных формулах табл. 9.27 нужно при шлицах по рис. 9.52, е слагаемые hш /bш заменить на 0,3 + 1,12 • 106 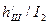 , по рис. 9.52, ж — на hш/bш + 1,12 • 106
, по рис. 9.52, ж — на hш/bш + 1,12 • 106  , где
, где  — толщина ферромагнитной перемычки над пазом, м; I2 — ток ротора, А.
— толщина ферромагнитной перемычки над пазом, м; I2 — ток ротора, А.
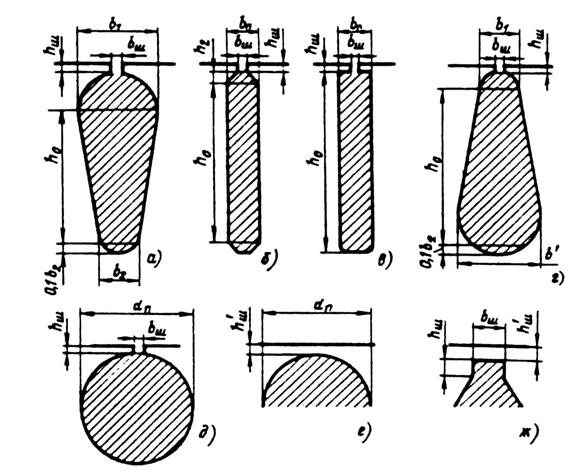
Рис. 9.52. К расчету коэффициентов магнитной проводимости
пазового рассеяния короткозамкнутых роторов:
а — д — полузакрытые пазы; е, ж — закрытые пазы
Коэффициент магнитной проводимости лобового рассеяния рассчитывают в зависимости от размеров и расположения замыкающих колец обмотки по следующим формулам.
В роторах с литыми обмотками при замыкающих кольцах, прилегающих к торцам сердечника ротора (см. рис. 9.37, б), используют формулу
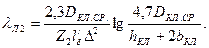
 (9.178)
(9.178)
Если замыкающие кольца отставлены от торцов ротора (см. рис. 9.37, а), как, например, в обмотке, выполненной из медных или латунных стержней, впаянных в замыкающие кольца, расчет проводят по формуле
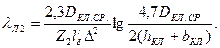 (9.179)
(9.179)
В этих формулах Dкл.ср — средний диаметр замыкающих колец по (9.171); Δ = 2 sin πρ/Z2 — коэффициент приведения токов в кольце к току в стержне; hкл и bкл — средние высота и ширина колец (см. рис. 9.37); 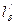 ; — по (9.154).
; — по (9.154).
Коэффициент магнитной проводимости дифференциального рассеяния обмотки, короткозамкнутого ротора
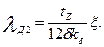 (9.180)
(9.180)
где
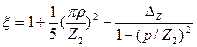 (9.181)
(9.181)
ΔZ находят по кривым рис. 9.51, а.
Как видно из (9.181), при большом числе пазов ротора, приходящихся на пару полюсов: Z2/p ≥ 10, без заметной погрешности можно принять ξ = 1.
Коэффициент проводимости скоса, учитывающий влияние на ЭДС обмотки ротора скоса пазов,
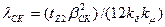 , (9.182)
, (9.182)
где βск — скос пазов, выраженный в зубцовых делениях ротора. При скосе пазов на одно зубцовое деление ротора βск = 1; kμ — коэффициент насыщения магнитной цепи (по 9.129).
Приведенное к числу витков обмотки статора индуктивное сопротивление обмотки короткозамкнутого ротора
х'2 = х2 γ12 (9.183)
где v12 — по (9.172).
Сопротивление схемы замещения rμ (см. рис. 9.47, а) является расчетным. Введением его в схему замещения учитывают влияние потерь в стали статора на процессы в асинхронной машине, поэтому значение сопротивления rμ должно быть принято таким, чтобы выделяющаяся в нем активная мощность была равна мощности, затрачиваемой на потери в стали в реальной машине и отнесенной к одной фазе. Таким образом, rμ = РСТ/(m I20a ), так как активные потери в стали определяются активной составляющей тока холостого хода ,I0а. Из схемы замещения rμ = 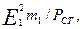 где
где 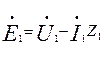 .
.
Сопротивление взаимной индукции обмоток статора и ротора xμ по схеме замещения может быть определено как xμ = Е1\Iμ.
В расчетной практике параллельное включение сопротивлений rμ и хμ оказалось удобнее заменить последовательно включенными сопротивлениями r12 и х12 (см. рис. 9.47, 6), значения которых определяют из условия
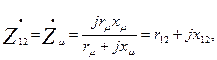
откуда
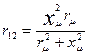 и
и 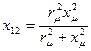
Так как в асинхронных машинах rμ ≤ xμ, то х12 ≈ хμ, а r12 << х12. В связи с этим значение r1 не играет заметной роли при анализе процессов в машине, и в расчетах им часто пренебрегают.
Сопротивления r1 и х12 с достаточной для обычных расчетов точностью определяют по следующим формулам:
r12 = Pcт.осн / (m I2μ) ; (9.184)
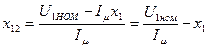 (9.185)
(9.185)
9.10.4. Относительные значения параметров
Для удобства сопоставления параметров отдельных машин и упрощения расчета характеристик параметры асинхронных машин выражают в относительных единицах, принимая за базисные значения номинальное фазное напряжение и номинальный фазный ток статора.
Значения параметров, выраженные в относительных единицах, отмечают звездочкой:
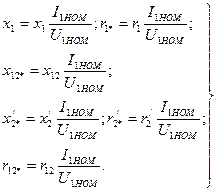 (9.186)
(9.186)
Относительные значения одних и тех же параметров схемы замещения различных асинхронных двигателей нормального исполнении незначительно отличаются друг от друга.
Так, относительные значения индуктивных сопротивлений рассеяния обмотки статора и приведенного сопротивления обмотки ротора большей частью находятся в пределах х1 = 0,08...0,14 и х'2 = 0,1...0,16.
Относительные значения сопротивлений взаимной, индукции, как правило, в 30—40 раз больше, чем x1*. Обычно х12* = 2...4.
Относительные значения активных сопротивлений обмотки статора и приведенного сопротивления обмотки ротора близки друг к другу и обычно составляют несколько сотых долей: r1* ≈ r'2* ≈ 0,02... 0,03; лишь, в машинах малой мощности их значения несколько увеличиваются.
Сопротивление r12* обычно составляет 0,05...0,2.
9.11. ПОТЕРИ И КПД
Потери в асинхронных машинах подразделяют на потери в стали (основные и добавочные), электрические, вентиляционные, механические и добавочные при нагрузке.
Основные потери в стали в асинхронных двигателях рассчитывают только в сердечнике статора, так как частота перемагничивания ротора, равная f2 = s f1, в режимах, близких к номинальному, очень мала и потери в стали ротора даже при больших индукциях незначительны [6].
В пусковых режимах f2 близка к f1 и потери в стали ротора соответственно возрастают, однако при расчете пусковых характеристик потери находят только для определения нагрева ротора за время пуска. Наибольшими потерями в пусковых режимах являются электрические потери в обмотках. Они во много раз превышают потери номинального режима, поэтому пренебрежение потерями в стали ротора при больших скольжениях не вносит сколько-нибудь заметной погрешности в расчет.
Основные потери в стали статоров асинхронных машин определяют в соответствии с (6.4) по следующей формуле:
Рст.осн = р1,0/50 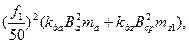 (9.187)
(9.187)
где p1,0/50 — удельные потери (табл. 9.28) при индукции 1 Тл и частоте перемагничивания 50 Гц; β — показатель степени, учитывающий зависимость потерь в стали от частоты перемагничивания; для большинства электротехнических сталей β = 1,3...1,5; kда и kдz —коэффициенты, учитывающие влияние на потери в стали неравномерности распределения потока по сечениям участков магнитопровода и технологических факторов. Для машин мощностью меньше 250 кВт приближенно можно принять kда = l,6 и kдz = 1,8; для машин большей мощности kда = 1,4 и kдz = 1,7; Ва и Вz1ср— индукция в ярме и средняя индукция в зубцах статора, Тл; mа, mz1 — масса стали ярма и зубцов статора, кг:
ma = π ( Da - ha ) ha l ст1 kc 1 γc ; (9.188)
mz 1 = hz 1 bz 1ср Z 1 l ст1 kc 1 γc ; (9.189)
hа — высота ярма статора, м:
h а = 0,5( Da - D) – h п1 ;
hz1 — расчетная высота зубца статора, м; bz 1ср — средняя ширина зубца статора, м:
bz 1ср = ( bz 1 max + bz 1 min )/ 2 ;
γс — удельная масса стали; в расчетах принимают γс = 7,8 • 103 кг/м3.
Таблица 9.28. Удельные потери в стали, Вт/кг, толщиной 0,5 мм
при индукции В = 1 Тл и частоте перемагничивания f = 50 Гц
| Марка стали | Удельные потери, Вт/кг | Марка стали | Удельные потери, Вт/кг |
| 2013 | 2,5 | 2312 | 1,75 |
| 2212 | 2,2 | 2412 | 1,3 |
| 2214 | 2 |
Добавочные потери в стали (добавочные потери холостого хода) подразделяют на поверхностные (потери в поверхностном слое коронок зубцов статора и ротора от пульсаций индукции в воздушном зазоре) и пульсационные потери в стали зубцов (от пульсации индукции в зубцах).
Для определения поверхностных потерь вначале находят амплитуду пульсации индукции в воздушном зазоре над коронками зубцов статора и ротора (рис. 9.53, а), Тл:
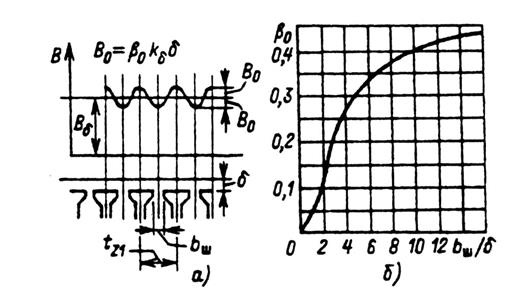
Рис. 9.53. К расчету поверхностных потерь в асинхронных машинах:
а — пульсация индукции в воздушном зазоре;
б — зависимость β0 =f /(bш / S)
B 01(2) = β01(2) kδ Bδ . (9.190)
Для зубцов статора β01 зависит от отношения ширины шлица пазов ротора к воздушному зазору: β01 = f (bш2 / δ); для зубцов ротора — от отношения ширины шлица пазов статора к воздушному зазору: β02 = f (bш1 / δ) . Зависимость β0 = f (bш / δ) приведена на рис. 9.53, б.
По В0 и частоте пульсаций индукции над зубцами, равной Z2n для статора и Z1n для ротора, рассчитывают удельные поверхностные потери, т. е. потери, приходящиеся на 1м2 поверхности головок статора и ротора:
для статора
Рпов1 = 0,5 k 01 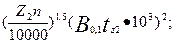 (9.191)
(9.191)
для ротора
Рпов2 = 0,5 k 02 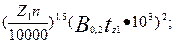 (9.192)
(9.192)
В этих выражениях k01(02) — коэффициент, учитывающий влияние обработки поверхности головок зубцов статора (ротора) на удельные потери; если поверхность не обрабатывается (двигатели мощностью до 160 кВт, сердечники статоров которых шихтуют на цилиндрические оправки), то k01(02) = 1,4...1,8, при шлифованных поверхностях (наружная поверхность роторов машин средней и большой мощности и внутренняя поверхность статора двигателей Р2 > 160 кВт) k01(02) = 1,7...2,0; n = nc (1 - s) ≈ nc — частота вращения двигателя, об/мин.
Полные поверхностные потери статора, Вт,
Рпов.1 = pпов.1 (t z 1 – b ш1 ) Z 1 l ст1. (9.193)
Полные поверхностные потери ротора, Вт,
Рпов2 = p пов2 (tz2 - b ш2 ) Z 2 l cт2. (9.194)
Для определения пульсационных потерь вначале находится амплитуда пульсаций индукции в среднем сечении зубцов Впул, Тл:
для зубцов статора
Впул1 = 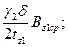 (9.195)
(9.195)
для зубцов ротора
Впул2 = 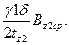 (9.196)
(9.196)
В этих формулах Bz1cp и Bz2cp — средние индукции в зубцах статора и ротора, Тл:
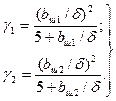 (9.197)
(9.197)
При открытых пазах на статоре или на роторе при определении γ1 и γ2 в (9.197) вместо bш1 или bш2 подставляют расчетную ширину раскрытия паза, равную:
b 'ш1(2) = 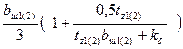 (9.198)
(9.198)
(индекс 1 при расчете b'ш1, индекс 2 при расчете b'ш2).
Значения коэффициента kδ в зависимости от отношения δп/δ для открытых пазов приведены на рис. 9.54.
Пульсационные потери в зубцах статора
P пул1 ≈ 0,11 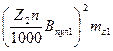 ; (9.199)
; (9.199)
пульсационные потери в зубцах ротора
P пул2 ≈ 0,11 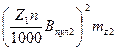 ; (9.200)
; (9.200)
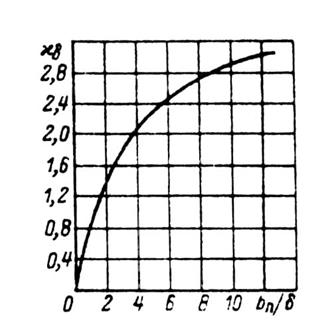
Рис. 9.54. К расчету пульсационных потерь
в асинхронных машинах
В этих формулах mz1 — масса стали зубцов статора, кг, определяется по (9.189); mz2 — масса стали зубцов ротора, кг:
mz 2 = Z 2 hz 2 bz 2ср l ст2 kc 2 γc (9.201)
где hz2 — расчетная высота зубца ротора, м; bz2cp — средняя ширина зубца ротора, м:
bz2 c p = (bz2 max + bz2 min ) / 2.
Поверхностные и пульсационные потери в статорах двигателей с и короткозамкнутыми или фазными роторами со стержневой обмоткой обычно малы, так как в пазах таких роторов bш2 мало и пульсации индукции в воздушном зазоре над головками зубцов статора незначительны. Поэтому расчет этих потерь в статорах таких двигателей не проводят.
В общем случае добавочные потери в стали
Рстдоб = Рпов1 + Рпул1 + Рпов2 + Рпул2 (9.202)
и полные потери в стали асинхронных двигателей
Pст = Рст.осн + Рст.доб. (9.203)
Обычно Рст.доб приблизительно в 5—8 раз меньше, чем Рст.осн.
Электрические потерн в асинхронных двигателях рассчитывают раздельно в обмотках статоров и роторов.
Электрические потери во всех фазах обмотки статора, Вт,
Pэ1 = m 1 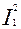 r 1. (9.204)
r 1. (9.204)
Электрические потери во всех фазах обмотки фазного ротора, Вт,
Рэ2 = m 2 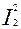 r 2 = m 1
r 2 = m 1 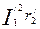 . (9.205)
. (9.205)
Электрические потери в обмотке короткозамкнутого ротора, Вт,
P э2 = m 2 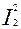 r 2 = Z 2
r 2 = Z 2 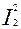 r 2 (9.206)
r 2 (9.206)
или
Рэ2 = m 1 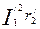 . (9.207)
. (9.207)
Электрические потери в щеточном контакте Рэ.ш, Вт, фазных роторов асинхронных двигателей, не имеющих приспособлений для подъема щеток и замыкания накоротко контактных колец при номинальном режиме работы,
Рэ.щ = m 2 ΔU щ I к.к, (9.208)
где ΔUщ — падение напряжения в скользящем контакте щетка — кольцо, В; принимается в зависимости от марки щеток по табл. П 4.2; Iк.к — ток в кольце, А; при соединении обмотки ротора в звезду Iк.к = I2 ; при соединении обмотки ротора в треугольник (при m2 = 3) Iк.к = 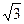 I2.
I2.
Механические и вентиляционные потери в асинхронных двигателях рассчитывают по приближенным формулам, полученным из опыта проектирования и эксплуатации двигателей. Коэффициент трения (Кт) учитывает конструкцию, скорость вращения, число пар полюсов, мощность двигателя. Его размерность изменяется в зависимости от вида формулы для определения Рмех (9.209 — 9.213).
Потери на трение в подшипниках и вентиляционные потери в двигателях с радиальной системой вентиляции без радиальных вентиляционных каналов, с короткозамкнутым ротором и вентиляционными лопатками на замыкающих кольцах, Вт,
Рмех ≈ Кт ( n / 1000)2 (10 D )3 ; (9.209)
Кт = 5 при 2р = 2; Кт = 6 при 2р ≥ 4 для двигателей с Da ≤ 0,25 м;
Кт = 6 при 2р = 2; Кт = 7 при 2р ≥ 4 для двигателей с Da > 0,25 м.
В двигателей с двигателях с внешним обдувом (0,1 ≤ Da ≤ 0,5 м)
Рмех = Кт ( n /10)2 D 4 a ; (9.210)
Кт = 1 для двигателей с 2р = 2 и Кт = 1,3(1 - Da) при 2р ≥ 4.
В двигателях с радиальной системой вентиляции средней и большой мощности
Рмех = 1,2  2 р τ3 ( n к +1,1)
2 р τ3 ( n к +1,1)  103 (9.211)
103 (9.211)
где nк — число радиальных вентиляционных каналов; при отсутствии радиальных каналов nк = 0.
В двигателях с аксиальной системой вентиляции
Рмех = Кт( n /1000)2 (10 D вент )3, (9.212)
где D вент — наружный диаметр вентилятора, м; в большинстве конструкций можно принять Dвент ≈ Da; Kт = 2,9 для двигателей с Da ≤ 0,25 м; Кт = 3,6 для двигателей с Da = 0,25...0,5 м.
В двигателях большой мощности (0,5 < Da < 0,9 м)
Рмех = Кт (10 Da )3 (9.213)
В этом выражении коэффициент Кт принимается по табл. 9.29.
Таблица 9.29. К расчету механических потерь
двигателей большой мощности
| 2p | 2 | 4 | 6 | 8 | 10 | 12 |
| Кт | 3,65 | 1,5 | 0,7 | 0,35 | 0,2 | 0,2 |
Потери на трение щеток о контактные кольца, Вт, рассчитывают для двигателей с фазными роторами при отсутствии приспособлений для подъема щеток и закорачивания контактных колец в номинальном режиме работы:
Ртр.щ = Ктр ρщ S щ υк, (9.214)
где Ктр — коэффициент трения щеток о контактные кольца (обычно принимается равным 0,16—0,17); ρщ — давление на контактной поверхности щеток, кПа (см. табл. П 4.2); Sщ — общая площадь контактной поверхности всех щеток, м2; vk — линейная скорость поверхности контактных колец, м/с.
Добавочные потери при нагрузке асинхронных двигателей возникают за счет действия потоков рассеяния, пульсаций индукции в воздушном зазоре, ступенчатости кривых распределения МДС обмоток статора и ротора и ряда других причин. В короткозамкнутых роторах, кроме того, возникают потери от поперечных токов, т. е. токов между стержнями, замыкающихся через листы сердечника ротора. Эти токи особенно заметны при скошенных пазах ротора. В таких двигателях, как показывает опыт эксплуатации, добавочные потери при нагрузке могут достигать 1...2 % (а в некоторых случаях даже больше) от подводимой мощности. ГОСТ устанавливает редкие расчетные добавочные потери при номинальной нагрузке, равные 0,5 % номинальной потребляемой мощности. При расчетах потерь и КПД двигателей в режимах, отличных от номинального, значение добавочных потерь пересчитывают пропорционально квадрату токов:
Рдоб = Рдоб.ном ( I 1 / I 1ном )2. (9.215)
Коэффициент полезного действия двигателя
η = Р2 /P1 = 1 - 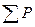 / P1, (9.216)
/ P1, (9.216)
где 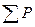 — сумма всех потерь в двигателе, Вт.
— сумма всех потерь в двигателе, Вт.
Ток холостого хода двигателя
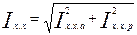 (9.217)
(9.217)
При определении активной составляющей тока холостого хода принимают, что потери на трение и вентиляцию и потери в стали при холостом ходе двигателя такие же, как и при номинальном режиме. При этом условии
I х.х.а = 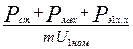 (9.218)
(9.218)
Электрические потери в статоре при холостом ходе приближенно принимаются равными:
Рэ1х.х = m I 2 μ r 1 . (9.219)
Реактивная составляющая тока холостого хода
I х.х.р ≈ Iμ (9.220)
Коэффициент мощности при холостом ходе
cos φ х.х = I х.х.а / I х.х. (9.221)








