9. 10. Параметры асинхронной машины
ДЛЯ НОМИНАЛЬНОГО РЕЖИМА
Параметрами асинхронной машины называют активные и индуктивные сопротивления обмоток статора r1, x1, ротора r2, х2 или приведенные к числу витков обмотки статора сопротивления ротора r'2 и х'2, сопротивление взаимной индуктивности х12 и расчетное сопротивление r12 (или rμ), введением которого учитывают влияние потерь в стали статора на характеристики двигателя.
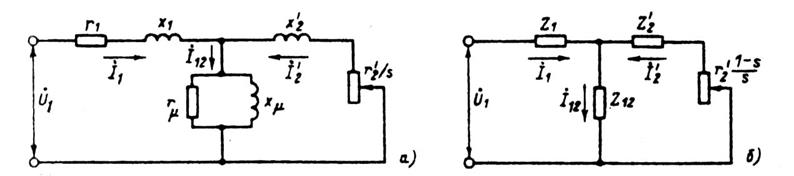
Рис. 9.47. Схемы замещения фазы обмотки приведенной асинхронной машины
Известные из общей теории электрических машин схемы замещения фазы асинхронной машины, основанные на приведении процессов во вращающейся машине к неподвижной, приведены на рис. 9.47. Физические процессы в асинхронной машине наглядно отражает схема, изображенная на рис. 9.47, а. Но для расчета оказалось удобнее преобразовать ее в схему, показанную на рис. 9.47, б.
Параметры схемы замещения не остаются неизменными при различных режимах работы машины. С увеличением нагрузки увеличивается поток рассеяния, и в связи с этим из-за возрастания насыщения отдельных участков магнитопровода полями рассеяния уменьшаются индуктивные сопротивления х1 и х2.
Увеличение скольжения в двигателях с короткозамкнутым ротором приводит к возрастанию действия эффекта вытеснения тока, что вызывает изменение сопротивлений обмотки ротора r2 и х2. При расчете рабочих режимов машины в пределах изменения скольжения от холостого хода до номинального эти изменения незначительны и ими обычно пренебрегают.
При расчете пусковых режимов, в которых токи машины в несколько раз превышают номинальный, а частота тока в роторе близка к частоте питающей сети, в большинстве случаев приходится учитывать изменение параметров от насыщения участков магнитопровода кода полями рассеяния и от влияния эффекта вытеснения тока.
9.10.1. Активные сопротивления обмоток статора и фазного ротора
Активные сопротивления r и r2, Ом, определяют по основной расчетной формуле (5.1):
r = kR ρυ 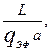 (9.132)
(9.132)
где L — общая длина эффективных проводников фазы обмотки, м; qэФ — площадь поперечного сечения эффективного проводника, м :
q эф = q эл n эл; (9.133)
qэл — площадь поперечного сечения элементарного проводника; nэл — число элементарных проводников в одном эффективном; а — число параллельных ветвей обмотки; ρυ — удельное сопротивление материала обмотки при расчетной температуре, Ом•м; kR — коэффициент увеличения активного сопротивления фазы обмотки от действия эффекта вытеснения тока.
В проводниках обмотки статора асинхронных машин эффект вытеснения тока проявляется незначительно из-за малых размеров элементарных проводников. Поэтому в расчетах нормальных машин, как правило, принимают kR = 1 . Некоторое увеличение потерь,
обусловленное действием эффекта вытеснения тока, относят к дополнительным потерям.
В обмотках фазных роторов kR также принимают равным единице независимо от размеров и числа проводников в пазу, так как частота тока в них при номинальном и близких к нему режимах очень мала.
Общая длина проводников фазы обмотки L, м,
L = l cp w, (9.134)
где l cp — средняя длина витка обмотки, м; w — число витков фазы. Среднюю длину витка lср находят как сумму прямолинейных пазовых и изогнутых лобовых частей катушки:
l ср = 2 ( l п + l л ). (9.135)
Длина пазовой части lп равна конструктивной длине сердечников машины:
l п = l 1(2).
Лобовая часть катушки имеет сложную конфигурацию (рис. 9.48). Точные расчеты ее длины и длины вылета лобовой части требуют предварительного определения всех размеров катушки и сопряжены со значительными объемами расчетов, данные которых в дальнейшем электромагнитном расчете обычно не используются. Для машин малой и средней мощности и в большинстве случаев для крупных машин достаточно точные для практических расчетов результаты дают эмпирические формулы, учитывающие основные особенности конструктивных форм катушек.
Катушки всыпной обмотки статора. Длина лобовой части, м,
l л = K л b кт + 2В; (9.136)
вылет лобовых частей обмотки, м,
l выл = K л b кт + В. (9.137)
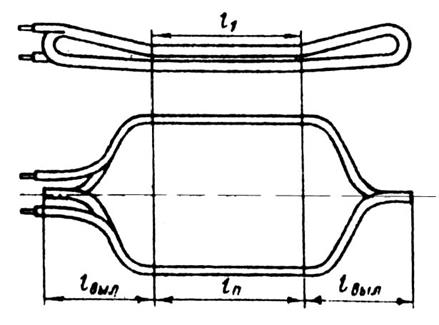
Рис. 9.48. Катушка двухслойной обмотки статора
В этих формулах bкт — средняя ширина катушки, м, определяемая по окружности, проходящей по серединам высоты пазов:
b кт = 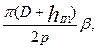 (9.138)
(9.138)
где β = урасч / τ — укорочение шага обмотки статора. Для диаметральных двухслойных обмоток, выполненных без укорочения шага, и для двухслойных обмоток, включая обмотки из концентрических катушек, имеющих разную ширину, принимают β = 1; Кл и Квыл — коэффициенты, значения которых берут из табл. 9.23 в зависимости от числа полюсов машины и наличия изоляции в лобовых частях; В — длины вылета прямолинейной части катушек из паза от торца сердечника до начала отгиба лобовой части, м.
Таблица 9.23. К расчету размеров лобовых частей катушек всыпной обмотки
|
Число полюсов 2р | Катушки статора
| |||
| Лобовые части не изолированы | Лобовые части изолированы лентой | |||
| Кл | Квыл | Кл | Лвыл | |
| 2 | 1,2 | 0,26 | 1,45 | 0,44 |
| 4 | 1,3 | 0,4 | 1,55 | 0,5 |
| 6 | 1,4 | 0,5 | 1,75 | 0,62 |
| ≥ 8 | 1,5 | 0,5 | 1,9 | 0,72 |
Для всыпной обмотки, укладываемой в пазы до запрессовки сердечника в корпус, берут В = 0,01 м. В машинах, обмотки которых укладывают после запрессовки сердечника в корпус, вылет прямолинейной части В = 0,015 м.
Катушки из прямоугольного провода. В обмотках статоров и фазных роторов асинхронных двигателей, выполненных из прямоугольного провода, длина лобовой части витка, м,
l л = Кл b кт + 2В + h п; (9.139)
вылет лобовой части обмотки (рис 9.49), м,
l выл = Кл b кт + В + 0,5 h п, (9.140)
где bкт, — средняя ширина катушки, для катушек статора рассчитывается по (9.138), для катушек ротора
b кт = 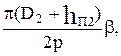 (9.141)
(9.141)
β — укорочение шага обмотки ротора; В — вылет прямолинейной части катушек из паза (по табл. 9.24); Кл, Kвыл — коэффициенты, определяемые из выражений
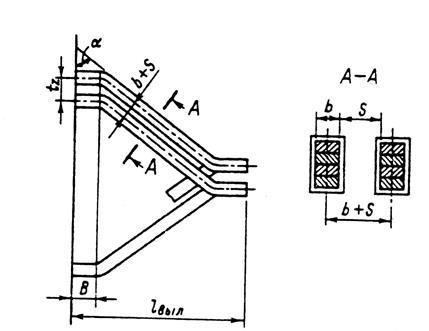
Рис. 9.49. Обозначения размеров катушек в лобовых частях
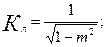 (9.142)
(9.142)
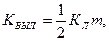 (9.143)
(9.143)
см. рис. 9.49.
Таблица 9.24. К расчету размеров лобовых частей катушек
обмотки из прямоугольного провода
| Напряжение U,B | S, 10-3, м | В, 10-3, м | Напряжение U, B | S, 10-3, м | В, 10-3, м |
| ≤ 660 | 3,5 | 25 | 6000...6600 | 6...7 | 35...50 |
| 3000...3300 | 5...6 | 35...40 | 10000 | 7.. .8 | 60…65 |
Примечание. Меньшие значения для катушек с непрерывной изоляцией.
m = sin α = ( b + S ) / tz; (9.144)
b — ширина меди катушки в лобовой части, м; S — допустимое расстояние между медью проводников соседних катушек (по табл. 9.24), м; tz — зубцовое деление, м.
Стержневая волновая обмотка фазных роторов асинхронных двигателей. Длина лобовых частей стержня ротора, м,
l л = Кл b кт + 2В c ; (9.145)
вылет лобовой части, м,
l выл = Кл b кт + Bc, (9.146)
где bкт — среднее расстояние между сторонами последовательно соединенных стержней:
b кт = ( D 2 - h п2 ) / 2р; (9.147)
Bc — сумма прямолинейных участков лобовой части стержня: длины вылета из паза и длины конца стержня в месте установки хомутиков, соединяющих стержни друг с другом. Обычно принимают 0,05...0,10 м (большие значения для машин большей мощности и напряжения). Для высоковольтных двигателей мощностью 800 - 1000 кВт и более берут Вс = 0,12...0,16 м.
Коэффициенты Кл и Квыл находят соответственно по формулам (9.142) и (9.143), в которых
m = ( bc т + Scт) / t z2, (9.148)
где Sст — расстояние между медью соседних стержней в лобовых частях, м (Sст принимают в соответствии с табл. 9.25 в зависимости от напряжения на контактных кольцах ротора при неподвижной машине); bcт — ширина меди стержня ротора, м; t'z2 — зубцовое деление по дну пазов ротора, м:
t' z 2 = π( D 2 – 2 h П2 ) / Z 2 (9.149)
Таблица 9.25. К расчету размеров лобовой части
стержней фазных роторов асинхронных двигателей
| Uк.к., В | 500 | 500...1000 | 1000.. .1500 | 1500.. .2000 |
| Sст, 10-3 м | 1,7 | 2 | 2,6 | 2,9 |
После расчета lп определяют среднюю длину витка по (9.135) и длину всех стержней фазы обмотки по (9.134).
Активное сопротивление фазы ротора r2 определяют по (9.132). Дня дальнейших расчетов r2 должно быть приведено к числу витков первичной обмотки
r '2 = v12 r2, (9.150)
где коэффициент приведения сопротивлений обмотки фазного ротора
v12 = 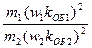 (9.151)
(9.151)
9.10.2. Индуктивные сопротивления обмоток двигателей
с фазными роторами
Индуктивные сопротивления обмоток статора и ротора двигателей с фазными роторами рассчитывают по формуле
x = 1,58 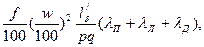 (9.152)
(9.152)
здесь расчетная длина l'δ при наличии радиальных вентиляционных каналов для обмотки статора
l 'δ = l 1 - 0,5 nk bk (9.153)
и для обмотки ротора
l 'δ = l 2 - 0,5 nk bk (9.154)
при отсутствии радиальных каналов в этих формулах nк = 0.
Входящие в (9.152) коэффициенты магнитной проводимости λп, λл и λд обмоток определяют следующим образом.
Коэффициент магнитной проводимости пазового рассеяния рассчитывают по формулам, приведенным в табл. 9.26, в зависимости от конфигурации паза и расположения в нем проводников обмотки (рис. 9.50). В этих формулах значения коэффициентов kβ и k'β зависят от укорочения шага обмотки β, которое определяют по расчетному шагу обмотки (см. гл. 3) β = урасч / τ.
При β = 1
kβ = k'β = 1 (9.155)
При обмотке с укорочением 2/3 ≤ β≤ 1
k'β = 0,25 (1 + 3β); (9.156)
при укорочении 1/3 ≤ β ≤ 2/3
k'β = 0,25 (6β - 1). (9.157)
Коэффициент
kβ = 0,25 (1 + 3 k'β). (9.158)
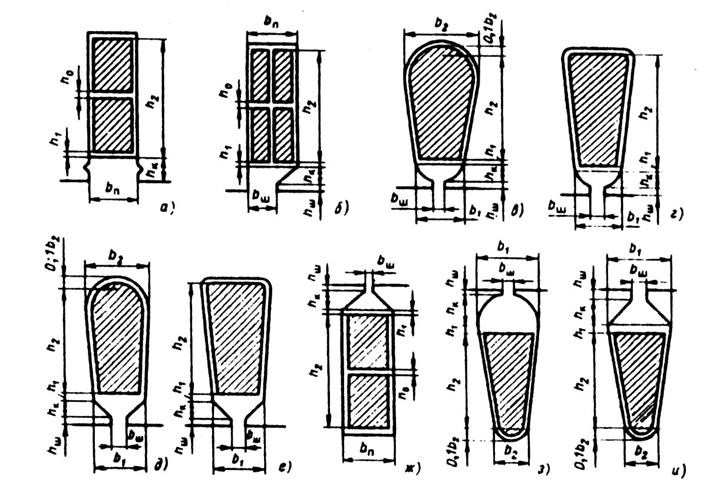
Рис. 9.50. К расчету коэффициентов магнитной проводимости пазового рассеяния
фазных обмоток:
а—е — обмотки статора; ж—и — обмотки фазного ротора
Таблица 9.26. Расчетные формулы для определения коэффициентов
магнитной проводимости пазового рассеяния обмоток статора и
фазного ротора асинхронных двигателей
| Рисунок | Тип обмотки | Расчетные формулы |
|
9.50, а | Двухслойная | 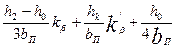
|
| Однослойная | 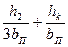
| |
| 9.50, б | Двухслойная | 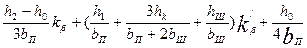 
|
| 9.50, в,г,з | Двухслойная и однослойная | 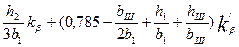
|
| 9.50, д,е,и | То же | 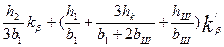
|
| 9.50, ж | Двухслойная | 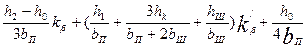
|








