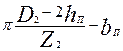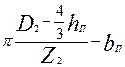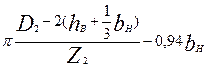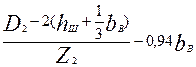9. 9. Расчет магнитной цепи

Дата: 2025-06-02; Просмотры: 9

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Расчет магнитной цепи проводят для режима холостого хода двигателей, при котором для асинхронных машин характерно относительно сильное насыщение стали зуб­цов статора и ротора. Как отмечено в гл. 4, насыщение зубцовых зон приводит к упло­щению кривой поля в воздушном зазоре (рис. 9.44). Пересечение реальной (уплощен­ной) кривой поля 2 в зазоре с основной гармонической 1 происходит в точках, отстоящих от оси симметрии одного полупериода кривой на угол 35°. Поэтому за расчетную индукцию принимается не амплитудное значение, а В_расч = В_max cos ψ ≈ В_max cos 35° ≈ 0,82 B_max. По В_расч следует

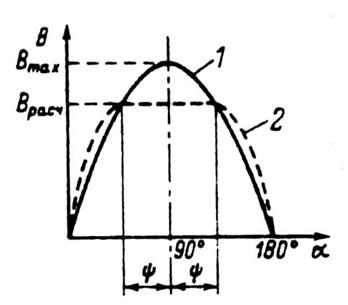
Рис. 9.44. Распределение индукции в воздушном

за­зоре асинхронного двига­теля:

1 — ненасыщенного (синусои­дальная кривая);

2 — насы­щенного (уплощенная кривая)

определить Н_расч по основной кривой намагничивания и увеличить затем результат в k = 1/ 0,82 раз, приведя напряженность к амплитудному значению индукции. Для воздушного зазора, имеющего линейную зависимость Н = f (B), эта операция равносильна непосредственному определению магнитного напряжения зазора по В_δ. При определе­нии магнитных напряжений участков магнитной цепи с нелинейны­ми магнитными характеристиками влияние уплощения учитывается специальными кривыми намагничивания для зубцов и ярм асинх­ронных двигателей, построенными по основной кривой намагничи­вания с учетом указанных зависимостей. При этом принимают

а_δ = 2/ π ≈ 0,637 и k_в = π / (2 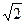) ≈ 1,11.

Марку электротехнической стали рекомендуется выбирать в за­висимости от высоты оси вращения проектируемого асинхронного двигателя:

Расчет магнитной цепи проводят в следующей последовательно­сти.

9.9.7. Магнитное напряжение воздушного зазора

Расчет магнитного напряжения воздушного зазора, как и всех последующих участков магнитной цепи, рекомендуется проводить на два полюса машины, т.е. вдоль замкнутой силовой линии потока полюса. Возможен также расчет на один полюс, при этом получен­ные по расчетным формулам данного параграфа магнитные напря­жения участков цепи F_i, необходимо уменьшить в 2 раза, а при опре­делении намагничивающего тока (см. ниже) суммарное магнитное напряжение всей цепи соответственно увеличить в 2 раза. Окончате­льный результат от этого не меняется.

Магнитное напряжение воздушного зазора, А,

F_δ = 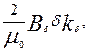(9.103)

где B_δ — индукция в воздушном зазоре, Тл, рассчитанная по (9.23) по окончательно принятому числу витков в фазе обмотки w₁ и обмоточ­ному коэффициенту k_об1 определенному для принятой в машине об­мотки; δ – воздушный зазор, м; k_δ – коэффициент воздушного зазора, рассчитанный по (4.15) или (4.16); μ₀ — магнитная проницае­мость: μ₀ = 4 • 10^-7 Гн/м.

9.9.2. Магнитное напряжение зубцовой зоны статора

Общая формула для расчета магнитного напряжения зубцовой зоны статора

F_{Z 1} = 2h_z1 H_z1, (9.104)

где h_z1 — расчетная высота зубца статора, м; H_z1 — расчетная напряженность поля в зубце, А. Напряженность поля в зубце определяют по кривым намагничивания для зубцов принятой при проектирова­нии марки стали (см. Приложения 1 и 2).

Расчетную высоту зубцов h_z1 и расчетную напряженность поля H_z1 определяют по-разному в зависимости от конфигурации зубцов, связанной с формой пазов статора.

Зубцы с параллельными гранями (в статорах с грушевидными или трапецеидальными пазами по рис. 9.29). Индукция в зубце

B_{Z 1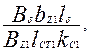} = (9.105)

где h_Z1 — расчетная ширина зубца, м, определяется по формулам табл. 9.15; если размеры b'_Z1 и b"_Z1 одинаковы, то b_z1 = b'_z1 = b"_z1; если размеры b'_Z1 и b"_z1 различаются менее чем на 0,5 мм, то b_z1 = 0,5(b'_z1 + b"_z1). При различии, превышающем 0,5 мм, следует либо скорректировать размеры паза, либо определить расчетную напряженность поля H_z1 как для зубцов с изменяющейся площадью поперечного сечения (см. ниже); k_с1 — коэффициент заполнения сталью сердечника статора (см. табл. 9.13).

Расчетная напряженность поля, А/м, H_z1 = f (B_z1).

Расчетная высота паза h_z1 определяется по табл. 9.17.

Магнитное напряжение зубцовой зоны

F_{Z 1} = 2 h_{Z 1} H_{Z 1.} (9.105a)

Зубцы с изменяющейся площадью поперечного сечения (в статорах с прямоугольными пазами по рис. 9.28). Расчетная высота зубца h_Z1 = h_П. Расчетная напряженность поля

H_z1 = ( H_{Z 1 max} + 4 H_{Z 1ср} + H_{Z 1 min} ) / 6, (9.106)

где H_z1max, H_z1min и H_z1ср — напряженности поля в наименьшем, наибольшем и среднем сечениях зубца, определяемые по индукциям в этих сечениях : B_Z1max, B_Z1min и B_z1cp = 0,5(B_Z1max + В_Z1min).

Индукции В_z1max и В_z1min рассчитывают по (9.105), подставляя в формулу вместо размера b_z1 соответственно наименьшее и наибольшее значения ширины зубца, м, рассчитанные по формулам табл. 9.15.

Магнитное напряжение зубцовой зоны, А,

F_z1 = 2h_z1 H_z1. (9.107)

Практикуют также определение расчетной напряженности по индукции в поперечном сечении зубца на расстоянии 1/3 высоты от его наиболее узкой части. В этом случае в (9.105) вместо b_z1 под­ставляют значение b_z1/3 (см. табл. 9.15). Расчетная напряженность поля в зубце Hz1 = Н _z1/3 = f B _z1/3 .

Если индукция в каком-либо одном или в нескольких сечениях зубца окажется больше 1,8 Тл, то необходимо учесть ответвление части потока зубцового деления Ф_tz = B_δ t_z1 l_δ в паз, при котором действительная индукция в зубце уменьшается по сравнению с рас­считанной по (9.105). Метод определения действительной индукции изложен в гл. 4. При его использовании коэффициенты k_П рассчиты­вают для каждого из сечений зубца, в котором индукция превышает 1,8 Тл, и соответствующего ему по высоте сечения паза. По значе­нию k_П и расчетной индукции определяют действительную индук­цию в данном сечении зубца.

В зубцах с параллельными гранями при индукции выше 1,8 Тл коэффициент k_П рассчитывают по соотношению площадей попереч­ных сечений зубца и паза на середине высоты зубца. В зубцах с из­меняющейся площадью поперечного сечения при определении рас­четной напряженности по B _z1/3 коэффициент k_П рассчитывают по соотношению площадей поперечных сечений зубца и паза на высоте 1/3 наиболее узкой части зубца. Это приводит к некоторой погреш­ности в определении расчетной напряженности поля в зубце, но при средних уровнях индукций, характерных для зубцовой зоны стато­ра, эта погрешность не оказывает заметного влияния на результаты расчета.

9.9.3. Магнитное напряжение зубцовой зоны ротора

Расчет магнитного сопротивления зубцовой зоны ротора зави­сит от формы пазов и типа ротора: фазный ротор или короткозамкнутый с одной обмоткой (беличьей клеткой) или короткозамкнутый ротор с двумя обмотками — рабочей и пусковой (ротор с двойной беличьей клеткой). К последнему типу относят также одноклеточ­ные короткозамкнутые роторы с одной беличьей клеткой, имеющие фигурные пазы — лопаточные или колбообразные, которые при расчете рассматривают как роторы с двойной беличьей клеткой.

Магнитное напряжение зубцовой зоны фазного и короткозамкнутого роторов с одной беличьей клеткой с прямоугольными или с тра­пецеидальными пазами (по рис. 9,32, а, б; 9.40 и 9.41, а). Общая фор­мула расчета магнитного напряжения

F_z2 = 2h_z2 H_z2. (9.108)

где h_z2 — расчетная высота зубца (по табл. 9.20), м; H_z2 — расчетная напряженность поля в зубце ротора, А/м.

Таблица 9.20. Размеры зубцов фазных и короткозамкнутых одноклеточных

роторов с прямоугольными и трапецеидальными пазами

Размер	Форма пазов ротора по рис. 9.40
	9.32, а; 9.42	9.32, 6	9.40, а, б	9.41, a
bZmax			—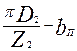
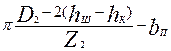
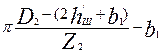
bZmin			—
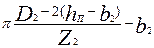
bZ1/3			—
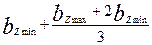
hZ	—	—	hП – 0,1 b2	hП – 0,1 b2
b'Z	—	—		—
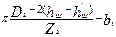
b''Z	—	—		—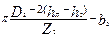

Расчетная напряженность поля H_z2 в зубцах с параллельными гра­нями (см. рис. 9.40, а, б), Тл, определяется в зависимости от индук­ции в зубце

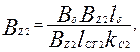(9.109)

где k_c2 — коэффициент заполнения сердечника ротора сталью (см. табл. 9.13); b_Z2 — ширина зубца ротора, м, определяется по формулам табл. 9.20.

Если расчеты b'_Z2 и b"_Z2 (табл. 9.20) дают одинаковые результаты, то b_z2 = b'_Z22 = b"_Z2. Если полученные размеры b'_Z2 и b"_Z2 различаются менее чем на 0,5 мм, то b_z2 = 0,5 (b'_Z2 + b"_Z2).

При различии, превышающем 0,5 мм, следует либо скорректиро­вать размеры паза с целью уменьшить это различие, либо опреде­лить расчетную напряженность поля как для зубцов ротора с изме­няющейся площадью поперечного сечения (см. ниже).

Расчетная напряженность поля в зубце

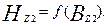
Расчетная напряженность поля в зубцах ротора с изменяющейся площадью поперечного сечения (по рис. 9.32; 9.41, а; 9.42). Расчетная напряженность поля определяется как средняя

H_Z2 = ( H _Z2max + 4 H _Z2cp + H _Z2min ) / 6, (9. 110)

где H_Z2max, H_Z2min, и H_Z2cp — напряженности поля в наибольшем, наи­меньшем и среднем сечениях зубца, определяемые по индукциям в этих сечениях зубцов В_Z2max, В_Z2min, и В_Z2cp = 0,5 (В_Z2max + B_Z2min).

Индукции B_z2max и B_z2min рассчитывают по (9.109), подставляя в эту формулу вместо размера b_Z2 соответственно наименьшее (b_z2min) и наибольшее (B_z2mах) значения ширины зубца, полученные по фор­мулам табл. 9.20.

При расчете магнитного напряжения по напряженности поля в сечении на 1/3 высоты зубца ротора находят индукцию В_Z1/3, под­ставляя в формулу (9.109) вместо b_z2 ширину зубца _bz1/3 (табл. 9.20). В этом случае расчетная напряженность

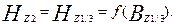
Если при расчете магнитного напряжения зубцов с переменным сечением H_Z2max > 2 H_Z2min, то более точные результаты дает деление зубца по высоте на две равные части и определение средних напряженностей в каждой из них в отдельности. В этом случае расчетная ширина зубца принимается на высоте 1/3 каждой части, т. е. на вы­соте, приблизительно равной 0,2 и 0,7 всей высоты паза от его наи­более узкой части:

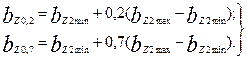(9.111)

Определив индукцию B_z0,2 и B_z0,7 в этих сечениях зубца, находят соответствующие им напряженности поля H_Z0,2 и H_Z0,7. Магнитное напряжение зубцовой зоны, А, в этом случае

F_z2 = h_z2 (H_z0,2 + H_{z 0.7} ), (9.112)

Необходимо отметить, что для всех сечений зубцов, расчетная индукция в которых превышает 1,8 Тл, необходимо определить действительную индукцию, т. е. учесть уменьшение потока в зуб­це за счет ответвления части потока зубцового деления в паз, как это указано в расчете зубцового напряжения зубцовой зоны ста­тора.

Магнитное напряжение зубцовой зоны ротора с фигурными паза­ми и с двойной беличьей клеткой. При фигурных пазах ротора или двойной беличьей клетке рассчитывают раздельно магнитные на­пряжения верхней и нижней частей зубцов, А:

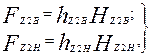(9.113)

где h_z2В и h_z2H — расчетные высоты верхней и нижней частей зубца, м, определяемые по формулам табл. 9.21 и 9.20; H_z2B и H_z2H — расчетные напряженности верхней и нижней частей зубца, А/м.

Расчет индукции для определения расчетных напряженностей Н_z2В и Н_z2H проводят по формулам, аналогичным приведенным выше для одноклеточных роторов, формулы для определения шири­ны зубцов в различных сечениях приведены в табл. 9.21 и 9.22 в зависимости от конфигурации пазов (рис. 9.45 и 9.46).

Магнитное напряжение зубцовой зоны роторов с фигурными пазами или с двойной беличьей клеткой, А/м,

F _{Z 2} = 2 (F_{z2 B} , + F_z2H). (9.114)

Учет ответвления потока в паз при индукциях выше 1,8 Тл при расчете магнитного напряжения так же обязателен, как и при расче­те зубцовых зон с другими конфигурациями пазов.

После расчета магнитных напряжений F_δ, F_z1 и F_z2 определяют коэффициент насыщения зубцовой зоны:

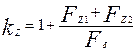(9.115)

Полученное значение k_z позволяет предварительно оценить пра­вильность выбранных размерных соотношений и обмоточных дан­ных проектируемой машины. Если k_z > 1,5...1,6, имеет место чрезмерное насыщение зубцовой зоны; если k_Z < 1,2, то зубцовая зона мало

Таблица 9.21. Размеры зубцов роторов асинхронных двигателей с фигурными пазами

Размер	Форма пазов ротора по рис. 9.40
	9.45, а	9.45, 6	9.45, в	9.45, г
bZmax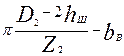
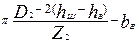
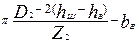
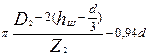
bZmin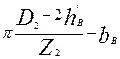
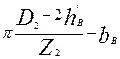
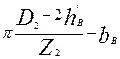
hZB	h'B	h'B	h'B	0,9 + hШ
bZн max		=		—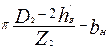
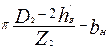bZн min		=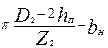
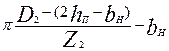
hZн	hH	hH – 0,1 bH	0,9 bH	—

Таблица 9.22. Размеры зубцов двойной клетки короткозамкнутых

роторов асинхронных двигателей

Размер	Форма пазов ротора по рис. 9.45
	9.46,а	9.45, 6	9.45, в
bZ в.ср
hZв	0,9 bВ + hШ
bZн max	—		—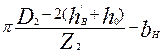
bZн min	—		—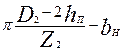
bZн ср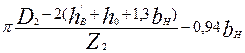
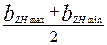
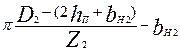
hZ Н	0,9 bH	h'H – h0	h'H – h0 – 0,1 bH2

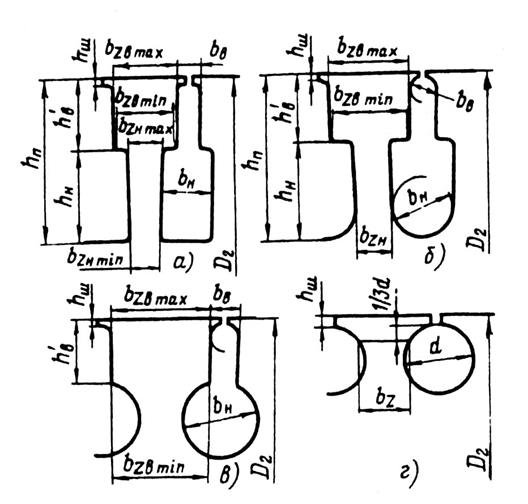
Рис. 9.45. Обозначение размеров зубцовой зоны короткозамкнутых роторов

с фигурными пазами: а —г — различные формы пазов ротора

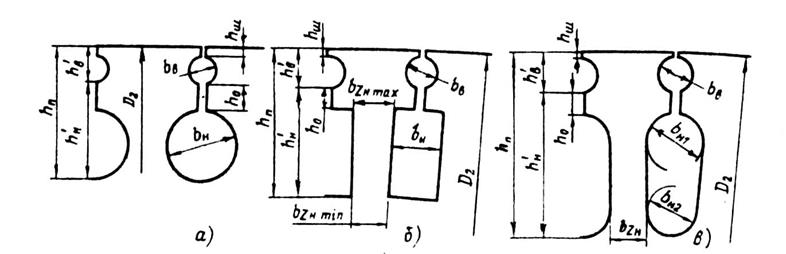
Рис. 9.46. Обозначения размеров зубцовой зоны

короткозамкнутых роторов с двойной беличьей клеткой:

а — в — различные конфигурации пазов двухклеточных роторов

использована или воздушный зазор взят слишком большим. В обоих случаях в расчет должны быть внесены соответствующие коррективы.

При дальнейшем расчете магнитной цепи определяют магнит­ные напряжения ярм статора и ротора.

9.9.4. Магнитное напряжение ярм статора и ротора.

Намагничивающий ток

Магнитное напряжение ярма статора, А,

F_a = L_a H_a, (9.116)

где L_a — длина средней магнитной силовой линии в ярме статора, м; Н_а — напряженность поля при индукции В_а по кривой намагничива­ния для ярма, принятой при проектировании стали, А/м.

Индукция в ярме статора, Тл,

В_а = Ф / (2 h ' _a l _ст1 k_{c 1} ), (9.117)

где h'_а — расчетная высота ярма статора, м:

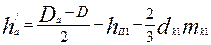(9.118)

где d_k1 и m_k1 — диаметр и число рядов аксиальных вентиляционных каналов в сердечнике статора; при отсутствии каналов m_k1 = 0.

Длина средней магнитной силовой линии в ярме статора, м,

L_a = (D_a - h_a) / (2p), (9.119)

где h_a — высота ярма статора, м:

h_a = (D_a - D) / 2 – h_п1. (9.120)

Магнитное напряжение ярма ротора, А,

F_j = L_j H_j (9.121)

где H_j — напряженность поля в ярме при индукции B_j по кривой намагничивания для ярма принятой при проектировании стали. Индукция в ярме ротора, Тл,

В_j = Ф / (2 h'_j l_ст2 k_c2 ), (9.122)

где k_с2 — коэффициент заполнения сталью ярма ротора (по табл. 9.13); h'_j — расчетная высота ярма ротора, м.

Для роторов с посадкой сердечника на втулку или на оребрен­ный вал (крупные асинхронные двигатели) расчетная высота ярма статора (см. рис. 9.43), м,

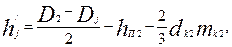(9.123)

В двигателях с непосредственной посадкой сердечника ротора на вал внутренний диаметр ротора равен диаметру вала: D_j = D_B. B таких двигателях с 2р = 2 или 4 учитывают, что часть магнитных силовых линий потока замыкается через вал. Поэтому в двигателях с 2р = 2 расчетную высоту ярма ротора, м, определяют из выра­жения

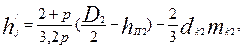. (9.124)

и длина силовых линий в ярме, м,

L_j = 2 h_j, (9.125)

где высота ярма ротора, м,

h_j = (D₂ - D _в ) / 2 - h _п2. (9.126)

В двигателях с 2р = 4 с непосредственной посадкой сердечника ротора на вал, имеющих размерные соотношения, при которых 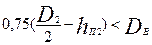, расчетную высоту ярма ротора определяют по (9.124), при других размерных соотношениях — по (9.126).

Длина средней магнитной силовой линии в ярме ротора всех двигателей, кроме двухполюсных, с непосредственной посадкой сер­дечника ротора на вал, м,

L_j = π ( D_j + h_j ) / (2 p ), (9.127)

где

h_j = (D₂ — D_j) / 2 — h_пa.

На этом расчет магнитных напряжений участков магнитной цепи двигателя заканчивается. Суммарное магнитное напряжение магнитной цепи (на пару полюсов), А,

F_u = F_δ + F _{z 1} + F_z2 + F_a + F_j. (9.128)

Коэффициент насыщения магнитной цепи

k_μ = F _u / F_δ. (9.129)

Намагничивающий ток, А,

I_μ ≈ 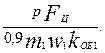(9.130)

Намагничивающий ток выражается также в процентах или в до­лях номинального тока двигателя:

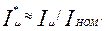(9.131)

Относительное значение I^*_μ служит определенным критерием правильности произведенного выбора и расчета размеров и обмот­ки двигателя. Так, если при проектировании четырехполюсного двигателя средней мощности расчет показал, что I^*_μ < 0,20.. .0,18, то в большинстве случаев это свидетельствует о том, что размеры машины выбраны завышенными и активные материалы недоиспользо­ваны. Такой двигатель может иметь высокие КПД и cosφ, но плохие показатели расхода материалов на единицу мощности, большие массу и габариты.

Если же в аналогичном двигателе I^*_μ > 0,3...0,4, то это в большин­стве случаев означает, что либо его габариты взяты меньшими, чем следовало, либо неправильно выбраны размерные соотношения участков магнитопровода. Двигатель будет иметь низкие КПД и cosφ.

В небольших двигателях мощностью менее 2...3 кВт I^*_μ может до­стигать значения 0,5...0,6, несмотря на правильно выбранные разме­ры и малое насыщение магнитопровода. Это объясняется относите­льно большим значением магнитного напряжения воздушного зазора, характерным для двигателей малой мощности [6].