Трение качения в высшей кинематической паре
Картину внешних сил и эпюр распределения давлений в месте контакта тел качения можно условно отобразить на нижеприведенных схемах. (рис.3.18.). В состоянии покоя эпюра напряжений в зоне контакта симметрична относительно общей нормали, проведенной через условную точку касания, а равнодействующая сила N совпадает с нормалью. При качении симметрия эпюры нарушается, а сила N смещается в направлении качения на расстояние k.
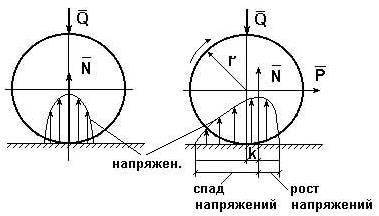
а) состояние покоя; б) состояние перекатывания
Рис.3.18. Примерные схемы сил и эпюр давления в зоне контакта цилиндра с плоскостью
Условные обозначения на схемах:
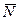 – равнодействующая сила давлений в месте смятия соприкасающихся звеньев (тел качения);
– равнодействующая сила давлений в месте смятия соприкасающихся звеньев (тел качения);
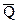 – нагружающая сила;
– нагружающая сила; 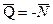 ;
;
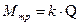 – момент трения качения,
– момент трения качения,
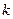 – плечо силы трения качения или коэффициент трения качения (имеет размерность длины),
– плечо силы трения качения или коэффициент трения качения (имеет размерность длины),
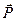 – сила перекатывания.
– сила перекатывания.
Условие равновесия перекатывающегося тела в форме моментов можно записать так: 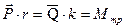 , откуда
, откуда 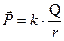 .
.
Величину 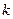 можно взять в инженерных справочниках.
можно взять в инженерных справочниках.
3.5.2. Пример учета сил трения при силовом анализе механизма
Пусть задан кривошипно – ползунный механизм с известными внешними силами (рис. 3.19). Необходимо провести силовой анализ механизма, учитывая силы трения в кинематических парах.
|
 | |||
 | |||
|
|
Рис.3.19. Кинематическая схема кривошипно – ползунного механизма
Последовательность решения следующая. Сначала проводим силовой анализ механизма без учета сил трения (см. примеры, приведенные выше). При этом также определяем силы реакций в кинематических парах. Затем обозначим силы реакций в кинематических парах, радиусы цапф валов и коэффициенты трения и занесем их в таблицу:
| Кинематические пары Параметры | О | А | Ввр. | Впост. |
| Силы реакций | R0 | RA | RB в p . | RB пост. |
| Радиусы цапф | r0 | rA | rB | - |
| Коэффициенты трения | f0 | fA | fB вр. | fB пост. |
Отразим трение в потерях мгновенных мощностей на трение в кинематических парах: вращательной - N = Мтр. × ω; поступательной - 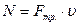 , где
, где
Мтр. = R × ρ = R × r × f – момент трения во вращательной кинематической паре,
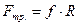 - сила трения в поступательной кинематической паре.
- сила трения в поступательной кинематической паре.
Применительно к кривошипно – ползунному механизму (рис.3.19) можно выразить потери мощностей на трение следующим уравнением:
N 0 + NA + N В вр. + NB пост. = Мтр. × ω1,
где N 0 , NA , N В вр. , NB пост. – соответственно потери мощности на трение в кинематических парах О, А, Ввр., Впост.,
ω, - угловая скорость кривошипа,
Мтр. – приведенный к кривошипу момент от всех сил трения в кинематических парах.
Тогда уравнение мощностей можно записать в следующем виде:
R 0 × r 0 × f 0 × ω1 + RA × rA × fA × (ω1 – ω2) + RB вр. × rB вр. × fB вр. × ω2 +
+ RB пост. × fB пост. × VB = M тр. × ω1.
Из этого уравнения определяем момент трения Мтр. на ведущем звене, который затем учитывается при расчете уравновешивающего момента Мур. или уравновешивающей силы Рур. на ведущем звене механизма.








