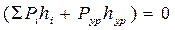Вариант 1. Ведущее звено – зубчатое колесо или кривошип
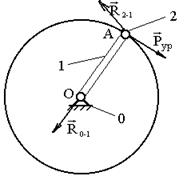
Рис. 3.9. План кривошипа с приложенными силами
На изображенном плане кривошипа (рис. 3.9) сила реакции в кинематической паре А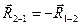 
.
Силу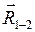 
берём из силового анализа, проведённого ранее для присоединённой к кривошипу структурной группы. Сила реакции 
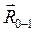|| OA (исходя из теоремы о трёх силах, в соответствии с которой линии сил, действующих на тело, находящееся в равновесии, пересекаются в одной точке. В данном случае это точка А).
Условие равновесия звена 1 (кривошипа):
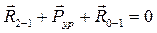. (3.6)
Строим план сил звена 1 в масштабе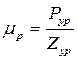 
(рис. 3.10), предварительно записав уравнение равновесия (3.6) в виде векторных отрезков:
.
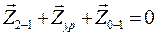Уравновешивающая сила вычисляется по формуле
,
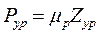а реакция в кинематической паре О - по формуле
,
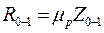где величины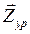 
и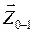 
берутся измерением на плане сил (рис. 3.10.)
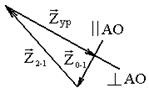
Рис. 3.10. План сил кривошипа
Вариант 2. Ведущее звено – муфта скольжения, совмещённая с кривошипом
В этом случае вместо уравновешивающей силы к ведущему звену приложен уравновешивающий момент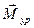 
(рис. 3.11).
|
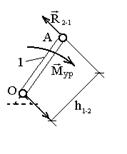
Рис. 3.11. План муфты с кривошипом
Уравнения равновесия ведущего звена 1:
,
,
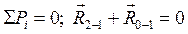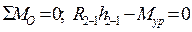где h 2-1 – плечо силы R 2-1 относительно оси вращения кривошипа О,
откуда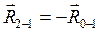 
, 
.
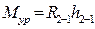Для нахождения величины плеча h 2-1 можно построить план звена в масштабе, нанести силы и провести необходимые измерения.
3.4. Теорема о «жёстком» рычаге Жуковского
Теорема используется для определения уравновешивающей силы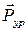 
или уравновешивающего момента 
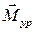без предварительного определения реакций в кинематических парах механизма.
Она является графической интерпретацией принципа возможных перемещений точек приложения сил. Для реального механизма эти возможные перемещения являются реальными.
Вывод теоремы
Исходя из принципа сохранения энергии сумма работ всех внешних сил, приложенных к звеньям механизма, равна нулю; это условие можно записать в виде
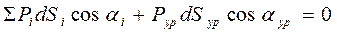, (3.7)
где Pi – все внешние силы, в том числе силы полезного и вредного сопротивления, силы инерции и веса, действующие на звенья механизма (силы реакции здесь не учитываются);
dSi – элементарные перемещения точек приложения этих сил;
a i – угол приложения внешних сил, или угол давления (угол между вектором силы и вектором скорости).
Разделим уравнение (3.7) на бесконечно малый интервал времени dt и получим (при условии, что dS / dt =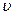 
)
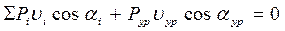, (3.8)
то есть сумма мгновенных мощностей равна нулю.
Для определения величины мгновенных мощностей можно также выполнить решение следующей графической интерпретации. Дано звено ВС с известной скоростью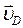 
точки D и приложенной к этой точке силой 
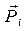(рис. 3.12). Построим план скоростей, повёрнутый на 900; здесь 
; 
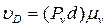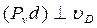. Вычислим момент силы 
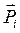относительно полюса Р v плана скоростей:
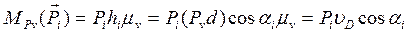. (3.9)
С учётом этого уравнение (3.8) можно записать так:
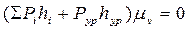. (3.10)
Так как масштаб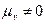 
, то можно сформулировать теорему Жуковского:
|
– запись теоремы Жуковского (3.11)
или: алгебраическая сумма моментов всех внешних сил, перенесенных с механизма в соответствующие точки повёрнутого на 900 плана скоростей, относительно полюса равна нулю.
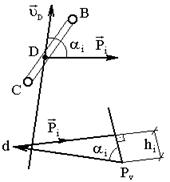
Рис. 3.12. План звена с повёрнутым на 900 планом скоростей
Последовательность определения P ур в механизме по теореме Жуковского:
1. Построить повёрнутый на 900 (в любую сторону) план скоростей механизма.
2. В соответствующие точки плана скоростей нанести все ранее определённые внешние силы (включая силы инерции и силы веса), действующие на механизм, в том числе и уравновешивающую силу P ур.
3. Составить уравнение вида (3.11). Плечи моментов сил брать из повёрнутого плана скоростей.
4. Из составленного уравнения определить P ур.
Пример
Заданы внешние силы, действующие на звенья механизма Р2 и Р3. Найдём уравновешивающую силу Рур. Для этого построим план механизма в масштабе длин (рис. 3.13) и повёрнутый на 900 план скоростей (рис. 3.14).
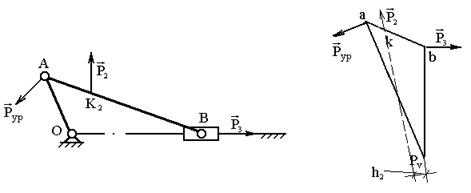
Рис. 3.13. План механизма Рис. 3.14. Повёрнутый на 900
план скоростей
Наносим силы в соответствующие точки k и b 3 повёрнутого плана скоростей, обозначаем плечи сил. Составляем уравнение моментов сил относительно полюса плана скоростей
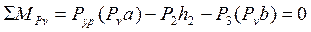, отсюда
.
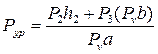Если силу P ур получим с отрицательным знаком, то её предварительно выбранное направление следует поменять на противоположное.
3.5. Силовой анализ механизма с учетом сил трения
3.5.1. Теоретические основы определения коэффициента трения