Прямая перпендикулярна плоскости, если она
перпендикулярна двум пересекающимся прямым
в этой плоскости.
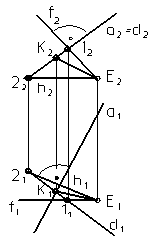На рис. 18 построена прямая ЕК, которая перпендикулярна прямой a и пересекает ее в точке К:
- взяли произвольную точку Е;
- через точку Е построили плоскость S(h Ç f ), заданную двумя пересекающимися прямыми; прямая h перпендикулярна прямой a (угол наклона прямой h к П1 a=0 и горизонтальная проекция h1 ^ a1), прямая f тоже перпенди-кулярна прямой a (угол наклона прямой f к П2 b=0 и фронтальная проекция f 2 ^ a2);
- определена точка К – пересечение прямой a с плоскостью S (в плоскости S взяли прямую d, фронтальная проекция которой d2 совпадает с фронтальной проекцией a2 прямой a; прямая d проходит через точку 1(11, 12), принадлежащую
Рис. 18 прямой f, и точку 2(21,22), принадлежащую прямой
22
h; горизонтальная проекция точки К1 – на пересечении горизонтальных проекций a1 и d1, фронтальная проекция - на линии связи к оси Х и на a2). Прямая ЕК перпендикулярна прямой a, т.к. ЕК лежит в плоскости S, перпендикулярной прямой a.
Через точку К в плоскости S можно построить веер прямых, которые будут перпендикулярны a.
На рис. 19 построена прямая MN, которая скрещивается с прямой g и перпендикулярна ей. С этой целью на прямой g взяли точку D и построили плоскость D, которая задана пересекающимися в точке D прямыми h и f.
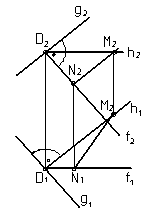
Обе прямые перпендикулярны прямой g
(ah = 0, h 1 ^ g1; bf = 0, f 2 ^ g2 ).
Если прямая принадлежит плоскости D и не проходит через точку D, то по отношению к прямой
g она будет скрещивающейся. У прямой MN фронтальная проекция M2N2 параллельна g2, а горизонтальная проекция M1N1 при продолжении пересекает g1, следовательно, прямые MN и g скрещиваются.
Любая прямая, которая расположена в плоскости D будет перпендикулярна прямой g.
При этом прямые, пересекающие прямую g,
Рис. 19 будут проходить через точку D.
1.8. Общий подход к решению задач
 |
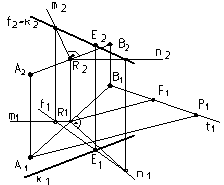Задача: На прямой К найти точку, равноудаленную от точек А и В
23
1. Определяется элемент, при использовании которого будет получен ответ на поставленную задачу:
Необходима точка Е на прямой k. Точку можно получить по определению 4 (ст. 7) при пересечении прямой k c некоторой прямой f, точки которой равноудалены от точек А и В.
2. Определяется множество элементов, из которого можно выбрать нужный:
Множеством таких прямых будет плоскость S, точки которой равноудалены от точек А и В.
3. Определить параметры плоскости S (база и углы наклона) по отношению к исходным элементам (точки А и В).
База плоскости (точка R) расположена на середине отрезка АВ.
Точку R(R1, R2) на отрезке АВ следует найти методом деления отрезка в заданном отношении n : m, что обеспечит математическую точность до любого знака после запятой. Для этого на горизонтальной плоскости проекций через горизонтальную проекцию точки В1 под произвольным углом к А1В1 проведем прямую t1, на которой от точки В1 отложим число единиц измерения n+m. Соединим конечную точку деления Р1 с А1. Через точку деления F1 проведем прямую F1R1 параллельно А1Р1. Фронтальная проекция точки R2 будет на линии связи и на фронтальной проекции А2В2.
Плоскость S задана пересекающимися в точке R прямыми m и n. Прямые m и n перпендикулярны прямой АВ (см. ст. 22. Взаимно перпендикулярные прямые).
4. Искомая точка Е – есть пересечение прямой k с f, которая принадлежит плоскости S (см. ст. 21. Взаимное положение прямой и плоскости).
2. Задачи для самопроверки знаний
 |
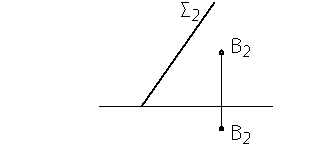1. Построить горизонтальный след плоскости, которая задана фронтальным следом и точкой
24
2. Определить угол наклона треугольника к П2
Определить натуральную величину треугольника АВС изменением угла b AВС
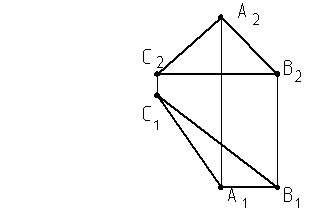
Почему линия пересечения плоскости треугольника D11 перпендикулярна оси Х и пересекается с D12 на оси Х.
3. Из точки D опустить перпендикуляр на плоскость треугольника АВС и определить расстояние от точки до плоскости.
 |
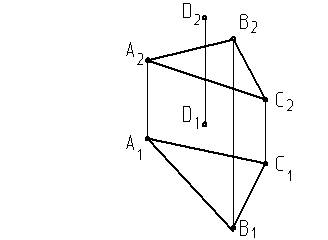25
4. Построить горизонтальную проекцию равностороннего треугольника АВС
25
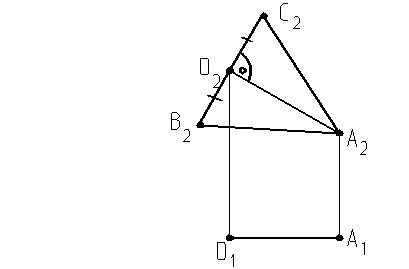
5. На прямой К найти точку, равноудаленную от А и В
 |
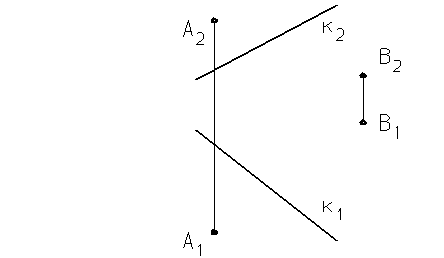26
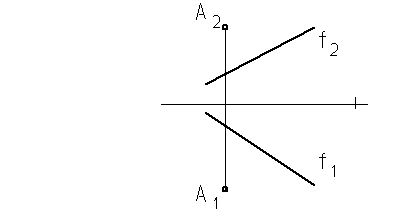
6. Определить расстояние от точки А до прямой f.
 |
 |
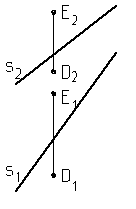7. Определить взаимное положение прямых.
27
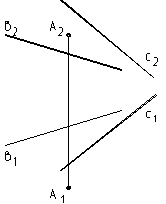
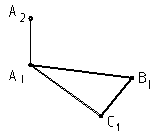
8. Построить треугольник АВС, если он 9. Через точку А провести прямую,
принадлежит плоскости D которая пересекает в и с
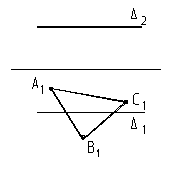
10. Определить взаимное положение 11. Построить плоскость АВС
плоскости q и прямой g под углом 60° к П1
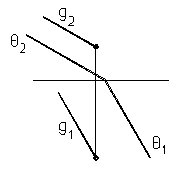
28
Литература
1. Тюкин, Н. Н. Инженерная и компьютерная графика : учеб. пособие . Ч. 1 / Н. Н. Тюкин, С. Г. Резико . – Вологда : ВоГТУ , 2009 . – 139, [1] с.
2. Тюкин, Н. Н. Инженерная и компьютерная графика : учеб. пособие . Ч. 2 / Н. Н. Тюкин, С. Г. Резико . – Вологда : ВоГТУ , 2009 . – 98, [2] с.
МИНОБРНАУКИ РОССИИ
федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Вологодский государственный университет»
Инженерная
и Компьютерная
графика