Плоскости параллельны, если две пересекающиеся прямые одной

Дата: 2025-06-02; Просмотры: 12

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

плоскости соответственно параллельны двум пересекающимся

прямым другой плоскости.

Через точку А проведем прямую АЕ, которая параллельна прямой СD.

В результате получим треугольник АВЕ, который параллелен прямой CD.

Прямая параллельна плоскости, если она параллельна прямой,

которая принадлежит плоскости.

В плоскости АВЕ возьмем прямую АР, угол b ^AР = 0. Измерим угол a^АЕ между А₂Р₂ и А₁Р₁, повернем фронтальные проекции С₂D₂, А₂В₂Е₂ вокруг оси Y^A на угол 90° - a^АЕ и перенесем в положение C¹₂D¹₂, А¹₂В¹₂Е¹₂ .

Горизонтальная проекция треугольника А¹₁В¹₁Е¹₁ – прямая, с ней совпадет горизонтальный след плоскости D¹₁. Горизонтальная проекция прямой C¹₁D¹₁ , которая будет параллельна А¹₁В¹₁Е¹₁. С C¹₁D¹₁ совпадет горизонтальный след S¹₁ плоскости, проходящей через CD и параллельной АВЕ.

19

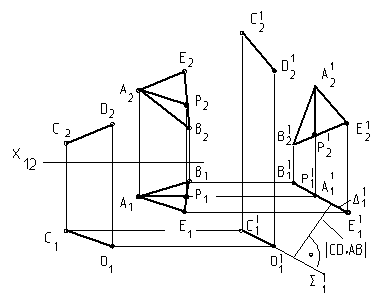Рис. 15

Расстояние между плоскостями _½D¹₁ S¹_1½ равно расстоянию между прямыми ½CD, AB½.

Угол между прямыми CD ^Ù AB равен углу между сторонами треугольника АВ ^Ù АЕ. Измерять угол следует в натуральной величине треугольника.

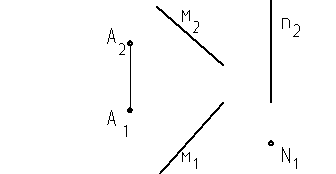Домашняя работа: Через точку А провести прямую АК, которая пересекает прямые м и n.

20

1.6. Взаимное положение прямой и плоскости

Прямая принадлежит плоскости :

- имеет 2 общие точки с плоскостью (в плоскости пересекает 2 прямые);

- имеет 1 общую точку с плоскостью и параллельна некоторой прямой, которая принадлежит плоскости.

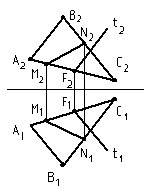
На рис. 16 прямая МN принадлежит плоскости треугольника АВС. Точки М и N лежат на соответственно на АС и ВС.

Прямая t принадлежит плоскости АВС, так как точка F лежит на прямой АС и прямая t параллельна стороне треугольника АВ ( t₂ парал-

Рис. 16 лельна А₂В₂, t₁ параллельна А₁В₁).

Прямая не принадлежит плоскости :

t параллельна плоскости, если она параллельна

прямой d, которая принадлежит плоскости,

t пересекает плоскость, то она пересекает

прямую d , которая принадлежит плоскости.

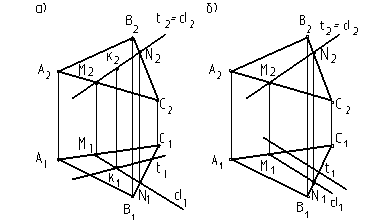На рис. 17а прямая t пересекает плоскость АВС в точке К, так как в

Рис. 17

этой точке прямая t пересекает прямую d, которая принадлежит плоскости.

21

Прямая d принадлежит плоскости, так как точки M и N принадлежат сторонам треугольника.

На рис. 17б прямая t параллельна плоскости так как t параллельна прямой d, которая принадлежит плоскости (d имеет с плоскостью общие точки M и N).

Примечание:

Прямую d, по отношению к которой определяется положение к плоскости прямой t, следует выбирать из условия, что d и t лежат в одной плоскости. В противном случае они не могут пересекаться.

Однозначно прямые лежат в одной плоскости, если:

1. Совпадают их фронтальные проекции (d₂ совпадает с t₂). Прямые лежат в плоскости, которая перпендикулярна П₂ .

2. Совпадают их горизонтальные проекции (d₁ совпадает с t₁). Прямые лежат в плоскости, которая перпендикулярна П₁ .

1.7. Взаимно перпендикулярные прямые

Две прямые взаимно перпендикулярны, если одна из них

принадлежит плоскости, перпендикулярной второй прямой