Двугранный угол между плоскостями (a Ù П1, b Ù П2, g Ù П3) измеряется линейным углом между линиями пересечения граней этого угла

Дата: 2025-06-02; Просмотры: 16

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

с третьей плоскостью, которая перпендикулярна данным

15

Плоскость треугольника D(АВС) на рис. 11 задана проекциями горизонтальной А₁В₁С₁ и фронтальной А₂В₂С₂.

Для определения, например, угла a можно изменить угол наклона АВС к плоскости П₂ до 90°. Треугольник АВС на плоскость П₂ спроецируется в прямую линю А¹₂В¹₂С¹₂ (рис. 11), с которой совпадет линия пересечения D¹₂ треугольника с плоскостью П₂. Плоскость П₁ перпендикулярна П₂ и плоскости пересекаются по оси Х₁₂.

Следовательно, угол a=D¹₂ ^Ù Х₁₂.

Две плоскости взаимно перпендикулярны, если одна

из них содержит перпендикуляр к другой плоскости.

Чтобы изменить угол ^A треугольника АВС, в нем надо взять прямую, угол b которой определяется на чертеже. Такой прямой может быть любая прямая, угол a которой = 0.

Возьмем прямую АD(A₂D₂, A₁D₁), координаты Z^A=X^D. A₁D₁ = AD. Следовательно, угол b ^AD = A₂D₂ ^Ù A₁D₁.

Повернем горизонтальную проекцию А₁В₁С₁ вокруг оси Z^A на угол 90° - b ^AD и перенесем в положение А¹₁В¹₁С¹₁. Проекция А¹₁D¹₁ ^ Х₁₂, при этом АD будет перпендикулярна П₂ и треугольник АВС ^ П₂. Фронтальная проекция А¹₂В¹₂С¹₂ совпадет с линией пересечения треугольника с фронтальной плоскостью D¹₂. Угол a^АВС будет измерен между D¹₂ ^Ù Х₁₂.

Натуральную величину треугольника можно найти, если расположить его, например, параллельно плоскости П₁. Повернем фронтальную проекцию А¹₂В¹₂С¹₂ треугольника вокруг оси Y^A1 на угол a^АВС и перенесем в положение А²₂В²₂С²₂ . Горизонтальные проекции точек А²₁В²₁С²₁ определим на пересечении линий связи к осям Х и Y. Треугольник будет параллелен П₁. Горизонтальная проекция треугольника А²₁В²₁С²₁ равна ½АВС½.

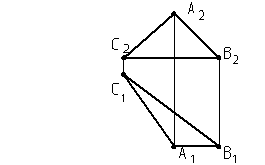
Домашняя работа

Определить углы a и b

треугольника АВС

16

1.4. Взаимное положение точки и прямой

Точка принадлежит прямой, если проекции точки расположены на одной линии связи и на соответствующих проекциях прямой.

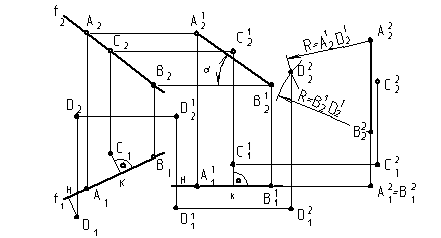Рис. 12

Точки А и В (рис. 12) принадлежат прямой f . А₂, В₂ и А₁, В₁ лежат соответственно на f₂ и f₁ и между собой на линиях связи.

Точки C и D по той же причине не принадлежат прямой f (обе проекции точки D не принадлежат одноименным проекциям прямой f , горизонтальная проекция C₁ не принадлежит горизонтальной проекции f₁).

Расстояние измеряется между точками. Следовательно, если прямую АВ расположить, например, перпендикулярно П₁, то горизонтальная проекция будет точка А²₁=В²₁. Расстояние от точки D до АВ будет равно D²₁ А²₁ .

Горизонтальная проекция прямой А₁В₁ и горизонтальные проекции точек D₁ и С₁ повернуты вокруг оси Z^A до положения, в котором Y^A = Y^B , угол b^АВ = 0 и перенесены в положение А¹₁В¹₁, D¹₁, С¹₁.

Чтобы сохранить геометрические размеры горизонтальной проекции

Объекта (прямая и 2 точки) в текущем положении 1, в исходном положении из горизонтальных проекций точек C₁ и D₁ опустим перпендикуляры C₁К и D₁Н на горизонтальную проекцию прямой А₁В₁. Для построения в первом текущем положении горизонтальной проекции точки С¹₁ от горизонтальной проекции точки А¹₁ отложено расстояние (А¹₁ К) = (А₁ К), из точки К восставлен

17

перпендикуляр (КС¹₁) = (КС₁). Для построения горизонтальной проекции

точки D¹₁ от горизонтальной проекции точки А¹₁ отложено расстояние (А¹₁Н)=(А₁Н), из точки Н восставлен перпендикуляр (НD¹₁)=(Н D₁).

Фронтальные проекции точек А¹₂ , В¹₂ , С¹₂ и D¹₂ расположены на пересечении линий связи к оси Х через точки А¹₁ , В¹₁ , С¹₁ и D¹₁ и линий связи к оси Z через точки А₂ , В₂ , С₂ и D₂.

На П₂ измерим угол a^АВ и повернем фронтальную проекцию в положении один на угол 90° - a^АВ вокруг оси Y^A1. Перенесем в положение 2. . Положение фронтальной проекции точки D²₂ определено расстояниями от концов фронтальной проекции отрезка (А²₂ В²₂) и находится на пересечении дуг радиусами R=(А¹₂ D¹₂ ) и R=(В¹₂ D¹₂ ). Аналогично построена фронтальная проекция точки С²₂.

1.5. Взаимное положение прямых

Параллельные прямые имеют одинаковые углы наклона к плоскостям проекций, но расстояние между ними не равно 0 (базовая точка одной прямой не принадлежит другой прямой). На рис. 13 прямая a (a₁ , a₂) и параллельная ей прямая е(е₁, е₂) заданы проекциями на плоскости П₁ и П₂.

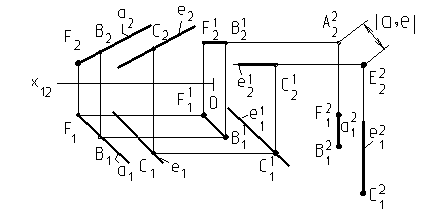
Если прямые параллельны, то параллельны их одноименные проекции (a_{1 ½½} е₁) и (a_{2 ½½} е₂) . Для параллельных прямых следует определить расстояние между ними.

Рис. 13

18

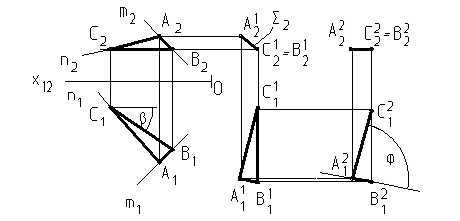
Пересекающиеся прямые имеют общую точку А, проекции которой лежат на одной линии связи к оси Х и совпадают с точками пересечения одноименных проекций, угол между прямыми j больше 0 (рис. 14).

Рис. 14

Скрещивающиеся прямые - не пересекаются (расстояние между ними не равно 0), не параллельны (угол между ними не равен 0). На плоском чертеже точки пересечения одноименных проекций не лежат на одной линии связи к оси Х (рис. 15).

При определении расстояния и угла между прямыми следует исходить из условия, что через две скрещивающиеся прямые можно всегда провести две параллельные плоскости.