Под самой прямой на плоской модели будем подразумевать проекцию, длина которой равна модулю.

Дата: 2025-06-02; Просмотры: 20
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

На основании (4): угол a = (MN)^(M1N1);

угол b = (MN)^(N2M2);

угол g = (MN)^(M3N3).

На рис. 9 прямая задана отрезком АВ. Построены проекции отрезка А1В1- горизонтальная, А2В2 – фронтальная и А3В3 – профильная. Если прямая бесконечна, то она пересекает горизонтальную плоскость П1 в точке М, фронтальную плоскость П2 в точке N и профильную плоскость П3 в точке Р. Точки пересечения прямой с плоскостями проекций называются следами.

 


 

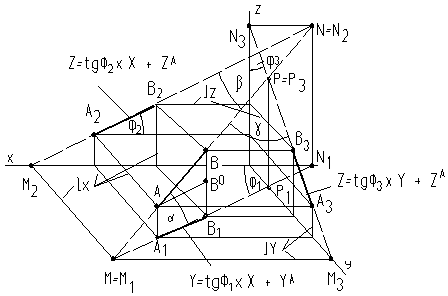Рис. 9

 

В пространстве точка пересечения прямой АВ, например, с горизонтальной плоскостью проекций П 1 будет точка М – пересечение АВ с ее горизонтальной проекцией А1В1.

На плоской модели прямоугольной системы координат сама прямая АВ отсутствует, есть только ее проекции А1В1, А2В2 и линии связи к оси Х l X.

 

11

Следовательно, можно построить только горизонтальную проекцию М1, которая совпадет с М, и фронтальную М2.

Уравнение точки М(Х, Y, Z=0). Если точка – пересечение двух прямых, то возможна система уравнений

 

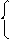Z=0 - линия, совпадающая с осью Х

Z=tg j2 ´ X + ZA - фронтальная проекция А2В2

 

Пересечение этих линий определит фронтальную проекцию М2 (X М, Z=0).

X М – расстояние от начала координат до М2.

 

Система уравнений для определения координаты Y точки М

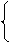X = X М - линия связи lx к оси Х через М2

Y=tg j1 ´ X + YA - горизонтальная проекция А1В1

 

Пересечение этих линий определит горизонтальную проекцию М1 (X М, Y М).

Y М – расстояние от оси Х до горизонтальной проекции М1.

 

Фронтальный след прямой АВ – точка N ( X , Y =0, Z ).

 

Система уравнений для определения координаты X точки N

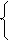
Y=0 - линия, совпадающая с осью Х

Y=tg j1 ´ X + YA - горизонтальная проекция А1В1

 

Пересечение этих линий определит горизонтальную проекцию N1 (X N, Y =0).

X N – расстояние от начала координат до N1.

 

Система уравнений для определения координаты Z точки N

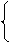X = X N - линия связи lx к оси Х через N1

Z=tg j2 ´ X + ZA - фронтальная проекция А2В2

 

Пересечение этих линий определит фронтальную проекцию N2 (X N, ZN).

Z N – расстояние от оси Х до фронтальной проекции N2.

 

Профильный след АВ – точка Р( X =0, Y , Z ).

 

Система уравнений для определения координаты Y точки P

 

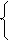X=0 - линия, совпадающая с осью Y

Y=tg j1 ´ X + YA - горизонтальная проекция А1В1

 

12

Пересечение этих линий определит горизонтальную проекцию P1 (X=0, YP ).

Y P – расстояние от начала координат до P1.

 

Система уравнений для определения координаты Z точки P

 

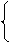Y = Y P - линия связи lY к оси Y через P1

Z=tg j3 ´ Y + ZA - профильная проекция А3В3

 

Пересечение этих линий определит профильную проекцию P3 ( YP, ZP).

Z P – расстояние от P3 до оси Y.

 

 

Длина отрезка и углы наклона к плоскостям проекций

 

Угол наклона к П1 a прямой АВ (рис. 9) измерен между горизонтальной проекцией А1В1 и самой прямой АВ.

 


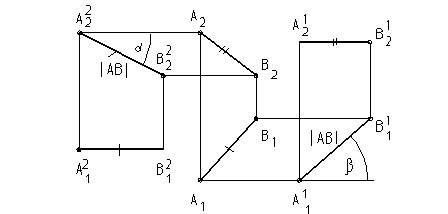Рис. 10

 

На рис. 10 прямая задана проекциями А1В1 и А2В2.

 

Угол наклона к П 1 a можно измерить между фронтальной и горизонтальной проекциями при условии, что А2В2 равна АВ.

А2В2 = АВ ´ Соs (b) (b – угол наклона АВ к П2)

 

Если угол b = 0, то Соs (b) =0 и А2В2 = АВ.

b = arctg(½YA - YB½ / A2B2)

13

Угол b = 0, если разность координат YA - YB = 0.

 

Перенесем горизонтальную проекцию во второе текущее положение А21В21 (изменятся координаты X и Y) и повернем вокруг оси ZA (рис. 3) до положения, в котором YA = YB . Координаты Z точек А и В при этом не изменятся, т. к. траектории вращения параллельны П1.

Фронтальные проекции точек А22, В22 будут на пересечениях линий связи к осям X и Z. Фронтальная проекция А22В22 = АВ.

Измерим a = А22В22 Ù А21В21.

Угол наклона к П 2 b можно измерить между горизонтальной и фронтальной проекциями при условии, что А1В1 равна АВ.

А1В1 = АВ ´ Соs (a)

Если угол a = 0, то Соs (a) =0 и А1В1 = АВ.

a = arctg(½ZA - ZB½ / A1B1)

Угол a = 0, если разность координат ZA - ZB = 0.

 

Перенесем фронтальную проекцию первое текущее положение А12В12 (изменятся координаты X и Z) и повернем вокруг оси YA (рис. 3) до положения, в котором ZA = ZB . Координаты Y точек А и В при этом не изменятся, т. к. траектории вращения параллельны П2.

Горизонтальные проекции точек А11, В11 будут на пересечениях линий связи к осям X и Y. Горизонтальная проекция А11В11 = АВ.

Измерим b = А11В11 Ù А12В12.

 

Домашняя работа

 

 

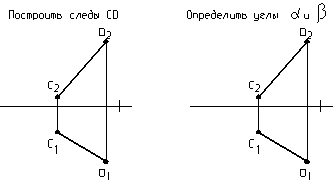
14

1.3. Плоскость

 

В общем виде плоскость задана двумя пересекающимися прямыми (2). Если на этих прямых взять 3 точки, не лежащие на одной прямой, то плоскость будет задана тремя точками. Если 3 упомянутые точки соединить прямыми, то плоскость будет задана треугольником (плоской фигурой в том числе окружностью, проходящей через три точки). Если через точку на первой прямой провести прямую, параллельную второй прямой, то плоскость будет задана двумя параллельными прямыми.

 

Параметры плоскости:

База, например, точка А(X, Y, Z) в треугольнике АВС (рис. 11).

Угол a - наклон треугольника к плоскости П1.

Угол b - наклон треугольника к плоскости П2.

Угол g - наклон треугольника к плоскости П3.

Перечисленные параметры считаются внешними, их изменение будет менять положение треугольника в пространстве относительно плоскостей проекций.

Натуральная величина треугольника – геометрические размеры (внутренний параметр плоскости).

 


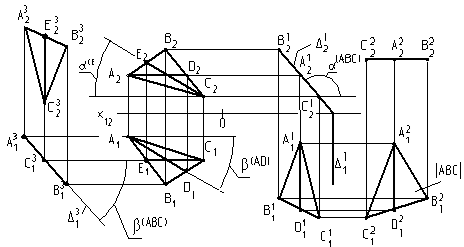Рис. 11