Следовательно, по проекциям объекта можно определить место его в пространстве и углы наклона к плоскостям проекций, а так же взаимное положение объектов.
И зображение объекта на плоскость - проекция объекта, обозначается именем объекта с индексом плоскости, на которой он изображен. БТ 1 ( X , Y , 0) - горизонтальная проекция точки БТ, БТ 2 ( X , 0, Z ) - фронтальная, БТ 3 (0, Y , Z ) - профильная.
На основании изложенного, возможна плоская модель трехмерного пространства, которая заменит при измерении длин и углов объемную модель.
Для формирования плоской модели введем определения:
- точка A - пересечение двух линий, обозначается
прописной буквой латинского алфавита; (4)
Математическое уравнение точки А(X, Y, Z). X, Y, Z – цифры, которые не имеют физического смыла, следовательно, их можно получить при решении системы двух уравнений, каждое из них имеет физический смысл, например, линий Y=f(X) и Z=f(X).
- плоскость Σ - две пересекающиеся прямые, обозначается
прописной буквой греческого алфавита; (5)
- отрезок ( AB ) – участок прямой между двумя точками . (6)
В соответствии с определением (5):
- прямые X и Y образуют горизонтальную плоскость П1 (рис. 4а), на ней изображаются только горизонтальные проекции, например, БТ1(X, Y);
- прямые X и Z образуют фронтальную плоскость П2 (рис. 4б), на ней изображаются только фронтальные проекции, например, БТ2(X, Z);
- прямые Y и Z образуют профильную плоскость П3 (рис. 4в), на ней изображаются только профильные проекции, например, БТ3(Y, Z).
Плоскости П1, П2, П3 называются основными плоскостями проекций, т.е. на них будем изображать расположенный в пространстве объект, например, точку БТ. При этом объект находится между наблюдателем и плоскостью проекций.
7
 |
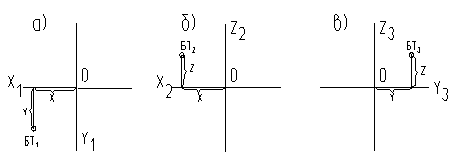Рис. 4
Чтобы получить проекцию точки, достаточно из нее опустить перпендикуляр на плоскость. Точка пересечения перпендикуляра с плоскостью - проекция точки на соответствующую плоскость.
 |
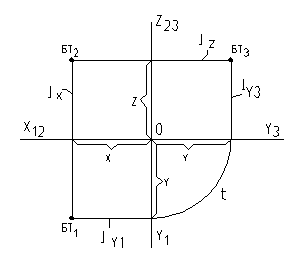Если три изображения рис. 4 совместить (наложить одно на другое), то получим плоскую модель прямоугольной системы координат (рис. 5).
Рис. 5
Оси X, Y и Z для различных плоскостей проекций совпадают, но отличаются линейным или угловым направлением.
8
Оси X1 (уравнение Y=0) и X2 (уравнение Z=0) совпадают, ось Y3 (уравнение X=0) совпадает с ними, но имеет противоположное направление.
Оси Z2 (уравнение X=0) и Z3 (уравнение X=0) совпадают, ось Y1 (уравнение X=0) совпадает с ними, но имеет противоположное направление.
Дуга t означает, что расстояние Y, отложенное по оси Y1 с некоторой степенью точности, перенесено на ось Y3 c той же погрешностью. Дуга t не принадлежит линии связи и ее можно заменить прямой под углом 45 °. В обеих случаях точка пересечения ly1 с осью y1 будет перенесена на ось y3 , через эту точку пройдет линия связи ly3 к оси y3.
Пример: Построить точку В(-20, -15, 25).
Построить точку - значит построить ее проекции в прямоугольной системе координат В(В1, В2, В3).
Если горизонтальная и фронтальная проекции имеют одинаковую координату х, то они лежат на одной линии связи к оси x (рис. 6). Для построения ее отложим по оси x координату X = -20 и проведем lX (X = -20 - математическое уравнение прямой lX .
По линии связи lX отложим от оси Х координату Z = 25, получим фронтальную проекцию В2. На той же линии связи отложим Y = -15, получим горизонтальную проекцию В1.
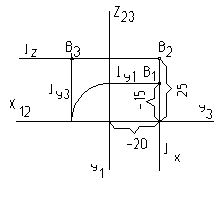Профильную проекцию В3
следует получить на пересечении линий связи к осям z и y lZ и ly3.
Если заданы проекции точки, то положение ее в реальном пространстве, например, в комнате, где расположен наблюдатель, можно описать следующим образом:
- поскольку координата X отрицательная, то точка находится за боковой стеной;
- поскольку координата Y отрицательная, то точка находится за фронтальной стеной;
- поскольку Z положительная, то точка находится над полом.
Рис. 6
Положение объекта в пространстве определено, если есть проекции его на 2 плоскости, например, П1 и П2 (рис. 7), т.е. известны координаты X = ½0lX½, Y = ½C1x12½, Z = ½C2x12½.
9
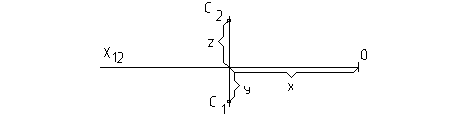
Рис. 7
Домашняя работа выполняются к очередному практическому
занятию.
Выполняются домашние и аудиторные работы на чертежной бумаге формата А4 (страница 51, литература [1]). На первом листе выполняется основная надпись типа рис.42, на остальных типа рис.44. (страница 52, литература [1]). При наличии методических указаний задачи можно выполнять непосредственно в них.
Задания:
1. Построить фронтальные проекции параллелепипеда в исходном и первом положениях (рис. 3). Построить профильную проекцию параллелепипеда в первом положении.
 |
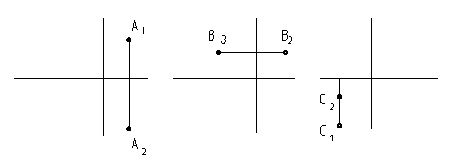2. Обозначить оси. Построить недостающие проекции точек А, В, С (Рис. 8).
Рис. 8
1.2. Прямая линия
Прямая в прямоугольной системе координат задается положением ее текущей базы, например, точкой A(X, Y, Z) и углами наклона к плоскостям проекций a к П1, b к П2, g к П3 (рис. 9).
10
Угол наклона прямой к плоскости измеряется между ( 7 )
самой прямой и ее проекцией на эту плоскость