Таким образом, прямая имеет положительное или отрицательное линейное направление.
ВВЕДЕНИЕ
Курс ’Начертательная геометрия. Инженерная и компьютерная графика’ входит в число дисциплин, составляющих основу инженерного образования.
Предметом начертательной геометрии является изложение и обоснование способов построения плоской модели трехмерного пространства и способов решения задач геометрического характера на базе этой модели. Однако, методы построения и преобразования чертежа преимущественно основаны на словесном описании и запоминании стандартных положений.
Такая трактовка трехмерного пространства не имеет явного сходства с положениями алгебры и тригонометрии, которые предлагают свою математическую модель трехмерного пространства.
Следовательно, начертательная геометрия в классической форме не предполагает использование ЭВМ, т.к. вычислительная техника воспринимает цифровую информацию с последующей математической обработкой ее в графическую. На базе графоматематической модели работают системы автоматизированного (с участием оператора) и автоматического управления объектами.
Одним из условий овладения техническими знаниями является умение читать (выполнять) конструкторские документы с учетом требований ЕСКД (единая система конструкторской документации) и СПДС (система проектной документации для строительства) и использовать при этом ЭВМ в режиме пользователя.
1. ГЕОМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ
В данной работе рассматривается один из вариантов геометрической модели трехмерного пространства, позволяющей использовать понятия начертательной геометрии на ЭВМ.
Аппарат геометрической модели предполагает измерение длин в метрах и плоских углов в градусах или радианах.
П од длиной подразумевается расстояние между двумя точками. Измерение длины ведется вдоль некоторой прямой от заранее выбранной на ней точки - текущей базы БТ (БТ - точка, координаты которой внутри объекта равны нулю) (рис.1).
Рис. 1. Прямая a. БТ - текущая база; a - обозначенное направление; L - положительное расстояние до точки С; ( -В ) - отрицательное расстояние до точки D.
3
Линия на чертеже обозначается строчной буквой латинского алфавита.
Если измерение длины ведется в обозначенную сторону прямой, то длина считается положительной и наоборот.
Таким образом, прямая имеет положительное или отрицательное линейное направление.
Кроме того, она имеет угловое направление. Измерение угла принято вести от тригонометрического нуля.
Т ригонометрический ноль – луч 0 с началом в БТ и направлен горизонтально вправо (рис.2) .
Измеряется угол до положительного направления прямой. Если измерение угла против часовой стрелки, то угол положительный, по часовой - отрицательный.
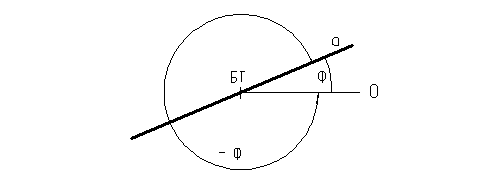О бозначается угол строчной буквой греческого алфавита.
Рис.2. Прямая a; j - положительный угол; (-j) - отрицательный угол; БТ – текущая база; 0 – тригонометрический ноль.
Математическая модель той же прямой Y = K ´ X + Y БТ (изменение координаты Y точки прямой с изменением координаты Х; K = tg j).
1.1. Прямоугольная система координат
Приняв прямую за единственный элемент для моделирования трехмерного пространства, можно тремя пересекающимися в одной точке и не лежащими в одной плоскости прямыми образовать трехмерное пространство, обеспечивая измерение в трех направлениях.
В прямоугольной системе координат три прямые X, Y и Z взаимно перпендикулярны и пересекаются в одной точке, которая совпадает с началом координат 0 (рис. 3).
4
Для работы в системе необходим аппарат, который позволял бы определять и изменять положение объекта в этом пространстве, т.е. измерять и изменять расстояния и углы.
 |
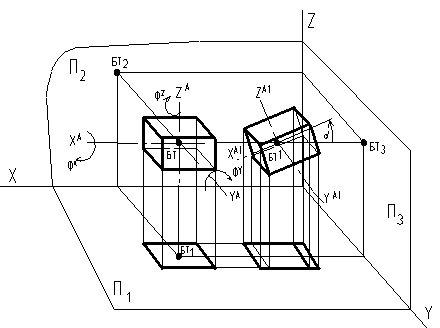Если принять точку БТ(X, Y, Z) за базу параллелепипеда, то положение его в пространстве можно определить расстояниями от базы БТ до плоскостей П1, П2, П3 и углами наклона граней к тем же плоскостям. БТ(X, Y, Z) – математическое уравнение точки.
Рис. 3
Если построить проекции БТ на плоскости плоскостей П1, П2, П3 соответственно БТ1, БТ2 и БТ3 и соединить проекции линиями связи (линия связи – ломаная линия, которая соединяет 2 проекции точки и перпендикулярна соответствующей оси), то:
координата X равна
расстоянию от БТ до П3 или
расстоянию от БТ до проекции БТ3 на П3 или
расстоянию от БТ2 до оси Z по линии связи к оси Z или
расстоянию от БТ1 до оси Y по линии связи к оси Y или
расстоянию от 0 до линии связи к оси Х;
5
координата Y равна
расстоянию от БТ до П2 или
расстоянию от БТ до проекции БТ2 на П2 или
расстоянию от БТ 1 до оси X по линии связи к оси X или
расстоянию от БТ3 до оси Z по линии связи к оси Z или
расстоянию от 0 до линии связи к оси Y;
координата Z равна
расстоянию от БТ до П1 или
расстоянию от БТ до проекции БТ1 на П1 или
расстоянию от БТ 2 до оси X по линии связи к оси X или
расстоянию от БТ3 до оси Y по линии связи к оси Y или
расстоянию от 0 до линии связи к оси Z.
Прямые XA, YA и ZA образуют внутреннюю прямоугольную систему координат объекта с базой в точке БТ. Если менять координаты БТ, то изменится положение объекта в пространстве (изменятся расстояния до плоскостей проекций).
На рис. 3 уменьшена координата Х базы параллелепипеда. В результате параллелепипед из исходного положения вместе с внутренней системой координат переместился вправо в 1 текущее положение (текущая база БТ1).
Объект можно вращать вокруг его внутренних осей координат. jХ – направление вращения вокруг оси ХА, jY - направление вращения вокруг оси YА, jZ - направление вращения вокруг оси ZА. При этом будут меняться углы наклона граней объекта к П1, П2, П3.
На рис.3 в 1 текущем положении параллелепипед повернут вокруг оси YA1 на угол a. На тот же угол изменилось направление осей XA1 , ZA1 и углы наклона граней к плоскостям П1 и П3. При этом на плоскостях П1 и П3 изменились геометрические размеры проекций, т.к. длина проекции прямой на плоскость П1
А1В1 = АВ ´ Cos a , (1)
длина проекции прямой на плоскость П3
А3В3 = АВ ´ Cos g . (2)
Угол наклона к П2 не изменился, т.к. ось вращения YA1 перпендикулярна данной плоскости проекций. Не изменяются и геометрические размеры проекции на плоскости П2, т. к. длины проекций прямых
А2В2 = АВ ´ Cos b. (3)
6
Длина проекции отрезка прямой на плоскость изменяется от 0 до натуральной величины отрезка (предел изменения Cos угла от 0 до 1).
a - угол наклона к горизонтальной плоскости.
b - угол наклона к фронтальной плоскости.
g - угол наклона к профильной плоскости.