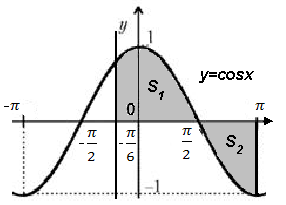
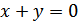Задание 2: Найти площадь криволинейной трапеции, ограниченной
линиями: у= cosx, у= 0, х =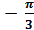 
, х = 
Решение.
Строим графики данных линий. (рис. 2).
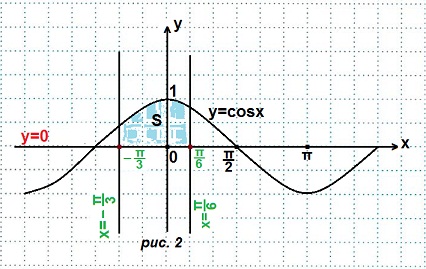
Площадь данной криволинейной трапеции:
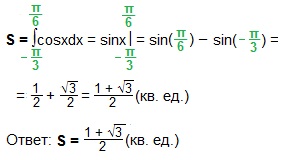
Задание 3: Найти площадь фигуры, ограниченной линиями
, 
, 
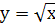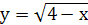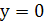
Решение:
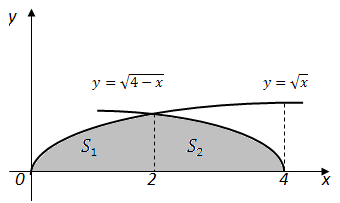
Вычислим абсциссы точек пересечения графиков этих функции ,для этого решим уравнение:
, 
, 
, 
.
, 
, 
,
, 
..
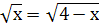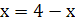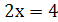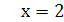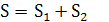
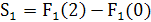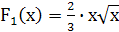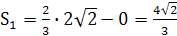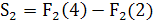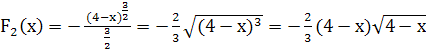
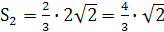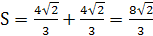(кв.ед).
Ответ: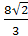 
(кв.ед).
Задание 4: Найти площадь фигуры, ограниченной графиком функции
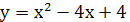и касательными к этому графику, проходящими через начало координат.
Решение .
Уравнение касательной к графику 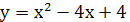проходящей через его точку 
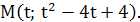Так как 
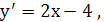то уравнение касательной имеет вид 
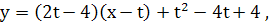или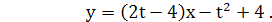 
По условию, начало координат принадлежит касательной, поэтому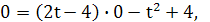 
откуда 
.
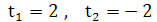Значение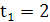 
соответствует касательной 
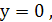точка касания 
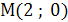. Значение 
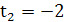соответствует касательной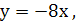 
точка касания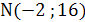 
. Площадь искомой фигуры равна сумме площадей криволинейных треугольников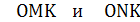 
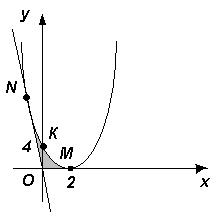
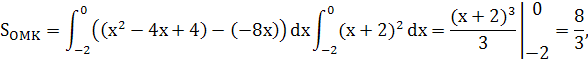
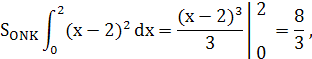
Искомая площадь равна 
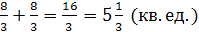
Задание 5: Найти площадь фигуры, ограниченной графиком функции
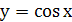, осью 
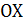и прямыми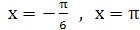 
Решение .
Данная функция состоит из двух криволинейных трапеций, расположенных в разных полуплоскостях относительно оси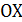 
.
Таким образом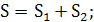 
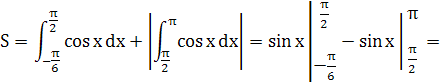
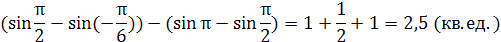
Задание 6: Найти площадь фигуры, ограниченной кривым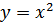и 
и
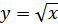
Решение.
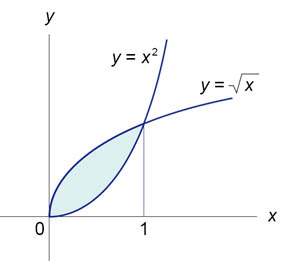
Рис.3
Сначала определим точки пересечения двух кривых (рис. 3).
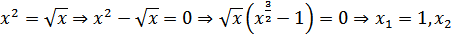=0
Таким образом, данные кривые пересекаются в точках (0,0) и (1,1). Следовательно, площадь фигуры равна
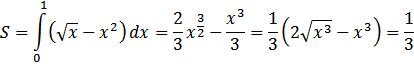
Проверочная работа:
Задание 1: Найти площадь фигуры, ограниченной линиями:
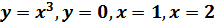
Задание 2: Найти площадь фигуры, ограниченной линиями:
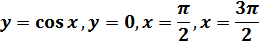
Задание 3: Найти площадь фигуры, ограниченной линиями:
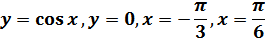
Задание 4 : Найти площадь фигуры, ограниченной осью ОХ и параболой
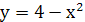
Задание 5: Найти площадь фигуры, ограниченной кривым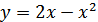и
и 