Геометрический смысл определенного интеграла
План работы:
1. Прочитать теорию.
2. Выписать правила в практическую тетрадь.
3. Выписать в практическую тетрадь решенные примеры.
4. Решить самостоятельно примеры проверочной работы (Чертеж обязательно!!!).
Криволинейной трапецией называют фигуру,
ограниченную графиком неотрицательной и непрерывной на отрезке 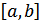 функции f, ОХ и прямыми х=а и х =b.
Теорема . Пусть f -непрерывная и неотрицательная на отрезке функции f, ОХ и прямыми х=а и х =b.
Теорема . Пусть f -непрерывная и неотрицательная на отрезке 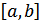 функция, а S - площадь соответствующей криволинейной трапеции . Tогда, если F есть первообразная для f на интервале , содержащем отрезок, то S=F(b)-F(a). функция, а S - площадь соответствующей криволинейной трапеции . Tогда, если F есть первообразная для f на интервале , содержащем отрезок, то S=F(b)-F(a).
|

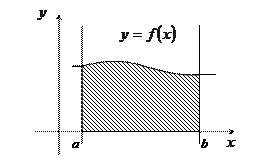
Криволинейная трапеция
Формулу для вычисления площади криволинейной трапеции с помощью интеграла можно записать таким образом:
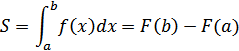 Формула верна для любой функции f , непрерывной на отрезке
Формула верна для любой функции f , непрерывной на отрезке 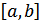 . .
|
Вычисление площадей плоских фигур
| S |
| a |
| b |
| x |
| 0 |
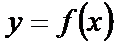
|
 Рис..1
Рис..1
|
| y |
1) Если функция 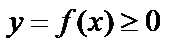 и непрерывна на отрезке
и непрерывна на отрезке 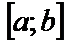 , то согласно геометрического смысла определенного интеграла площадь S под кривой
, то согласно геометрического смысла определенного интеграла площадь S под кривой 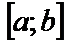 численно равна определенному интегралу
численно равна определенному интегралу
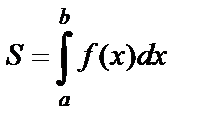 ,
, 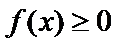 . (1)
. (1)
| Рис..2 |
| a |
| b |
| x |
| 0 |
| y |
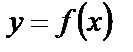
|
| S |
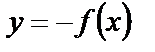
|
2) Если функция 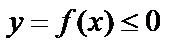 и непрерывна на отрезке
и непрерывна на отрезке 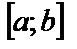 , то отображая ее график относительно оси абсцисc, получим кривую, которая имеет уравнение
, то отображая ее график относительно оси абсцисc, получим кривую, которая имеет уравнение 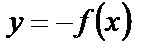 . Последняя функция уже неотрицательна на
. Последняя функция уже неотрицательна на 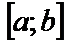 , а площадь под этой кривой на
, а площадь под этой кривой на 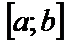 , из условия симметрии графиков, равна искомой площади S под кривой
, из условия симметрии графиков, равна искомой площади S под кривой 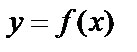 на
на 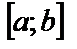 . Тогда имеем
. Тогда имеем
| y |
| b |
| c |
| a |
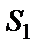
|
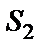
|
| x |
| Рис. 3 |
| 0 |
| d |
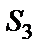
|
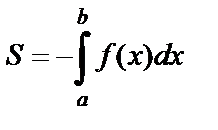 ,
, 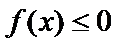 . (2)
. (2)
3) Если функция 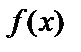 на отрезке
на отрезке 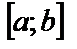
непрерывна и принимает как положительные
так и отрицательные значения, например, на
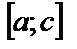 и
и 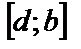
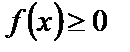 , а на
, а на 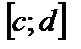
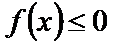 , то глядя,
, то глядя,
на рассмотренные случаи 1) и 2), имеем
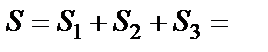
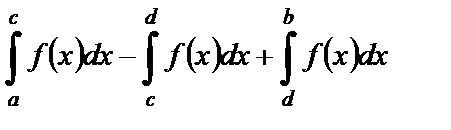 . (3)
. (3)
4) Если на отрезке 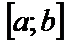 заданы две непрерывные функции
заданы две непрерывные функции 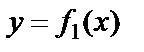 и
и 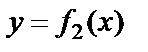 такие, что
такие, что 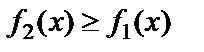 , тогда площадь S фигуры, ограниченной этими кривыми на отрезке
, тогда площадь S фигуры, ограниченной этими кривыми на отрезке 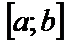 , вычисляется по формуле
, вычисляется по формуле
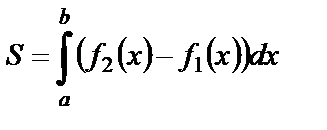 . (4)
. (4)
Возможны несколько случав размещения кривых на отрезке 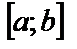 . Для всех изображенных случаев размещения кривых
. Для всех изображенных случаев размещения кривых 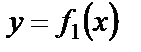 и
и 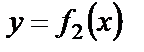 имеет место формула
имеет место формула 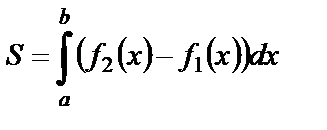
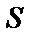
|
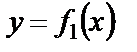
|
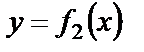
|
| a |
| b |
| x |
| y |
| 0 |
| Рис..4 |
| y |
| a |
| b |
| x |
| 0 |
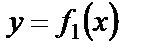
|
|
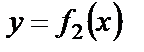
|
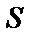
|
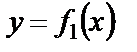
|
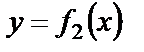
|
| y |
| a |
| b |
| x |
| 0 |
Задачи на вычисление площадей плоских фигур

| Задачи на вычисление площадей плоских фигур решают по следующему плану: 1. Делают схематический чертёж по условию задачи. 2. Составляют формулу для вычисления площади полученной фигуры и находят пределы интегрирования из условия задачи. 3. Вычисляют площадь фигуры по составленной формуле. |
Задание 1: Найти площадь криволинейной трапеции,
ограниченной линиями: 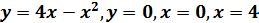
Решение
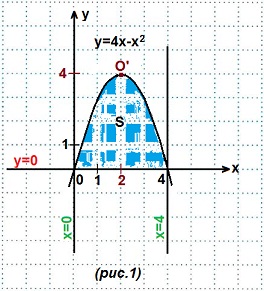
Строим графики данных линий. (рис. 1).
1) y=4x-x² — парабола (вида y=ax²+bx+c).
Запишем данное уравнение в общем виде: y=-x²+4x. Ветви этой параболы направлены вниз, так как первый коэффициент а=-1<0.
Вершина параболы находится в точке O′(m; n), где
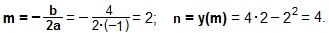
Значит О′(2; 4 вершина параболы.).
Нули функции (точки пересечения графика с осью Ох) найдем из уравнения:
4х-х²=0.
х(4-х)=0.
Отсюда, х=0 или х=4.
Абсциссы точек найдены, ордината равна нулю — искомые точки: (0; 0) и (4; 0).
2) y=0 — это ось Ох;
3) х=0 — это ось Оy;
4) х=4 — прямая, параллельная оси Оy и отстоящая от нее на 4 единичных отрезка вправо.
Площадь построенной криволинейной трапеции находим по формуле Ньютона-Лейбница.
У нас
f (x)=4x-x²,a=0, b=4.
Следовательно, искомая площадь равна