Тест по теме «треугольники»
ТЕСТ ПО ТЕМЕ «ТРЕУГОЛЬНИКИ»
1. Три точки, не лежащие на одной прямой, соединенные отрезками, образуют геометрическую фигуру:
а) треугольник
б) угол
в) нет правильного ответа.
2. В равных треугольниках против равных сторон лежат равные ………………
а) стороны
б) углы
в) нет правильного ответа.
3. Утверждение, справедливость которого устанавливается путем рассуждений, называется:
а) признаком
б) доказательством
в) теоремой.
4. Утверждение «Если две стороны и угол одного треугольника равны двум сторонам и углу другого треугольника, то такие треугольники равны», является:
а) первым признаком равенства треугольников
б) вторым признаком равенства треугольников
в) нет правильного ответа.
5. Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется:
а) медианой
б) биссектрисой
в) высотой.
6. В равнобедренном треугольнике:
а) углы при основании равны
б) биссектриса, проведенная к основанию, является медианой и высотой
в) стороны равны.
7. Утверждение « Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум углам другого треугольника, то такие треугольники равны», является:
а) первым признаком равенства треугольников
б) вторым признаком равенства треугольников
в) нет правильного ответа.
8. Третий признак равенства треугольников называется:
а) по сторонам и углу
б) по трем сторонам
в) нет верного ответа
9. Из третьего признака равенства треугольников следует, что треугольник – фигура:
а) непрочная
б) прочная
в) жесткая
10. Продолжи фразу: « Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой и ………………………………………………………………………………….»
11. Отрезок, соединяющий две точки окружности называется:
а) радиусом
б) диаметром
в) хордой.
12. Хорда, проходящая через центр окружности, называется:
а) радиусом
б) диаметром
в) хордой.
13. Любые две точки окружности делят ее на:
а) две части
б) пополам
в) два круга.
14. Построй угол на прямой а, равный данному при помощи циркуля и линейки:
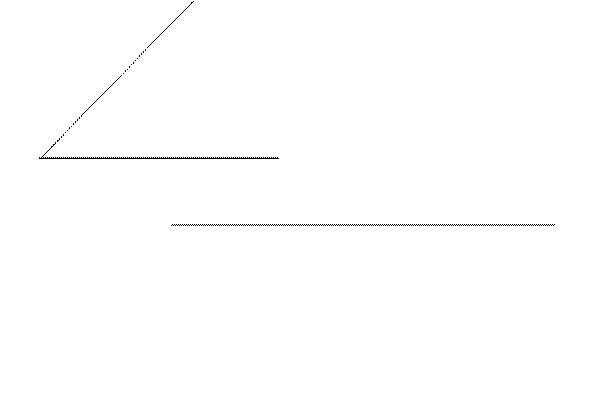
С помощью циркуля и линейки постройте биссектрису данного угла: