Обоснование: Определение. Умножением натуральных чисел называется алгебраическая операция, обладающая свойствами… &62, стр.243, 2 свойство
56 Установление взаимно однозначного соответствия между элементами непустого конечного множества А и отрезком натурального ряда называется
a) Теоретико-множественной характеристикой множества А
b) Классом конечных равномощных множеств
c) Отношением порядка на множестве А
d) Счетом элементов множества А
e) Другой ответ
Обоснование: Из определения. Установление взаимно однозначного соответствия между элементами непустого конечного множества А и отрезком натурального ряда называется счетом элементов множества А. &68, стр.260
57 В аксиоматической теории разностью натуральных чисел а и в называется натуральное число c, удовлетворяющее условию:
a) в+с=а
b)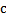 
c) а+с=в
d)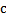
e) другой ответ
Обоснование: По определению. Вычитанием натуральных чисел a и b называется операция, удовлетворяющая условию: a - b = c тогда и только тогда, когда b + c = a . &64, стр.249
58 Запишите, используя символику, коммутативный закон сложения для натуральных чисел:
a)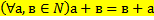 
b)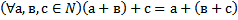 
c)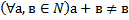 
d)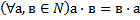 
e)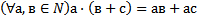 
Обоснование: &61, стр.241, Теорема 5. Доказательство данной теоремы состоит их 2х частей. И он доказывает коммутативный закон сложения натуральных чисел
59 Запишите, используя символику, ассоциативный закон умножения для натуральных чисел:
a)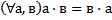 
b)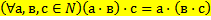 
c)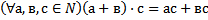 
d)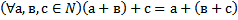
e) Для любых натуральных чисел a, b, c,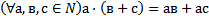 
Обоснование:&62, стр.245, теорема 10.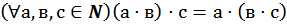 
Это свойство ассоциативности умножения.
60 Не выполняя вычислений, определите значения каких выражений будут равны
a)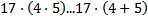 
b)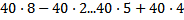 
c)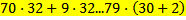 
d)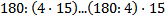 
e)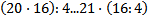 
Обоснование: Для начала вынесем с левой части уравнения общий множитель, и получаем 32 ⋅ (70+9)=79 ⋅ (30+2), если упростить выражение , то получится 32*79=79*32, а это коммутативный закон умножения , следовательно они равны.
61 Сложением натуральных чисел называется алгебраическая операция, обладающая двумя свойствами, второе свойство записывается так
a) Для любых натуральных чисел а и в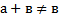 
b) Для любых натуральных чисел а и в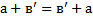 
c) Для любых натуральных чисел а и в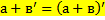 
d) Для любых натуральных чисел а и в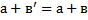 
e) другой ответ
Обоснование: По определению, &61 , стр.237
62 При аксиоматическом построении системы натуральных чисел в качестве основного взято отношение:
a) «следовать за»
b) «непосредственно следовать за»
c) «непосредственно предшествовать»
d) «предшествовать»
e) другой ответ
Обоснование: В качестве основного понятия при аксиоматическом построении арифметики натуральных чисел взято отношение «непосредственно следовать за», заданное на непустом множестве N . &60, стр.233
63 Вторая аксиома Пеано формулируется так:
a) В множестве N существует элемент, непосредственно не следующий ни за каким элементом этого множества. Называют его единицей.
b) Для каждого элемента а из N существует не более одного элемента, за которым непосредственно следует а.
c) Пусть множество М есть подмножество множества N и известно, что единица содержится в М; и из того, что а содержится в М, следует, что и а’ содержится в М. Тогда множество М совпадает с множеством N
d) Для каждого элемента а из N существует единственный элемент а’, непосредственно следующий за а.
e) Прямая разделяет плоскость на две полуплоскости
Обоснование: &60, стр. 233, 2 аксиома
64 В аксиоматической теории отношение «меньше» определено следующим образом:
a)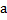 
b)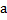
c)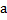
d)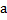
e) другой ответ.
Обоснование:
65 Отношение «меньше» на множестве натуральных чисел обладает свойствами:
a) Рефлексивность, симметричность и транзитивность;
b) Рефлексивность, антисимметричность и транзитивность;
c) Рефлексивность, антисимметричность и связанность;
d) Антисимметричность, транзитивность и связанность;
e) Симметричность, антисимметричность и транзитивность.
Обоснование:&63, теорема 12 - выражает свойство связанности отношения «меньше»; теорема 13 - выражает свойство транзитивности отношения «меньше»; теорема 14 - выражает свойство антисимметричности отношения «меньше» на стр.246
66 Умножением натуральных чисел называется алгебраическая операция, определенная на множестве натуральных чисел и обладающая двумя свойствами, второе свойство записывается так
a) Для любых натуральных чисел а и в а·в'=ав+а
b) Для любых натуральных чисел а и в а·в'=(а·в)'
c) Для любых натуральных чисел а и в а·в'=ав+а
d) Для любых натуральных чисел а и в а·в'=(а·в)'
e) Для любых натуральных чисел а и в а·в'=ав+в
Обоснование: Из определения в &62, стр.243
67 Назовите в порядке выполнения преобразований свойства сложения, которые используются при нахождении значения выражения 23+(19+7)=23+(7+19)=(23+7)+19=30+19=49
a) коммутативное свойство сложения и дистрибутивность слева относительно сложения
b) ассоциативное свойство сложения и коммутативное свойство сложения
c) дистрибутивность справа относительно сложения и ассоциативное свойство сложения
d) коммутативное свойство сложения и ассоциативное свойство сложения
e) дистрибутивность слева относительно сложения и коммутативное свойство сложения
Обоснование. &61, стр. 241 Сначала была выполнена теорема 5, затем теорема 4 стр.240: a+(b+c)=a+(c+b)=(a+c)+b
68 Отрезком натурального ряда N4 является множество:
a) {1,3,5,7} c) {1,2,3,4} e) {10,11,12,13}
b) {2,3,4,5} d) {1,2,4,5}
Обоснование: По определению. Отрезком Na натурального ряда называется множество натуральных чисел, не превосходящих натурального числа а. Таким образом, у нас задано N 4 , следовательно и множество будет состоять из {1,2,3,4}
69 Из перечисленных свойств множества натуральных чисел выделите свойство дискретности:
a) Из всех натуральных чисел единица является наименьшим числом.
b) Ни для одного натурального числа а нет такого натурального числа n, что а<n<а+1
c) Множество натуральных чисел – упорядоченное множество, т.к. отношение «меньше» для натуральных чисел транзитивно и антисимметрично
d) Множество натуральных чисел бесконечно
e) Любое непустое подмножество множества натуральных чисел содержит наименьшее число.
Обоснование: Ни для одного натурального числа а не существует такого натурального числа что а< n <а+1. Это свойство называется свойством дискретности множества натуральных чисел. &63, стр.248
70 На множестве натуральных чисел алгебраической является операция:
a) Пересечение c) Вычитание e) Сложение
b) Деление d) Объединение
Обоснование: По определению. Сложением натуральных чисел называется алгебраическая операция, обладающая некоторыми свойствами .&61, стр.237
71 Если один из множителей увеличить в 5 раз, а второй уменьшить в 5 раз, то произведение
a) Увеличится в 5 раз
b) Не изменится
c) Уменьшится в 5
d) Увеличится в 25 раз
e) Уменьшится в 25
Обоснование: Определение. Умножением натуральных чисел называется алгебраическая операция, обладающая свойствами… &62, стр.243
По свойствам мы знаем, что если увеличить (или уменьшить) множитель в несколько раз, то и произведение увеличится (или уменьшится) во столько же раз.
Общий пример: a * b = c
По условию задания сначала увеличили один из множителей в 5 раз, и получили 5 a . Затем второй уменьшили в 5 раз и получили b/5. Таким образом, произведение не изменилось : 5 a * b /5= c (т.к 5 и 1/5 сокращаются при умножении)
72 Третья аксиома Пеано формулируется так:
a) Прямая разделяет плоскость на две полуплоскости
b) Для каждого элемента а из N существует единственный элемент а', непосредственно следующий за а.
c) Пусть множество М есть подмножество множества N и известно, что: единица содержится в М и из того, что а содержится в М, следует, что и а' содержится в М. Тогда множество М совпадает с множеством N.
d) Для каждого элемента а из N существует не более одного элемента, за которым непосредственно следует а..
e) В множестве N существует элемент, непосредственно не следующий ни за каким элементом этого множества. Называют его единицей.
Обоснование: &60, стр. 233, 3 аксиома
73 Назовите в порядке выполнения преобразований свойства, которые используются при нахождении значения выражения 17·25+75·17=17·25+17·75=17·(25+75)=17·100=1700
a) коммутативное свойство умножения и дистрибутивность слева относительно сложения
b) коммутативное свойство сложения и дистрибутивность слева относительно сложения
c) ассоциативное свойство умножения и коммутативное свойство умножения
d) дистрибутивность справа относительно сложения и ассоциативное свойство умножения
e) дистрибутивность слева относительно сложения и коммутативное свойство умножения
Обоснование: : &62, стр.245 Сначала была выполнена теорема 11, затем теорема 9: a*b+c*a=a*b+a*c=a*(b+c)
74 Законы умножения натуральных чисел в аксиоматической теории доказываются:
a) методом полной индукции
b) методом от противного
c) методом математической индукции
d) с использованием дедуктивного вывода
e) другой ответ
Обоснование: Метод математической индукции - данный метод доказательства, основан на аксиоме 4(с.252) его можно использовать при доказательстве свойств сложения и умножения, можно применять и для доказательства других утверждений о натуральных числах. 67, стр.257