Обоснование: Определение. Умножением натуральных чисел называется алгебраическая операция, обладающая свойствами… &62, стр.243
Общий пример: a * b = c
По условию мы каждый множитель умножаем на 3 : (а*3)*( b *3)=3а*3 b =9 c . Таким образом, мы видим, что произведение увеличится в 9 раз.
Пример: 5*3=15; 15*9=135; и 135:15=9
45 Если уменьшаемое увеличить в 4 раза и вычитаемое увеличить в 4 раза, то разность
a) Увеличится в 8 раз
b) Увеличится в 4 раза
c) Не изменится
d) Увеличится в 16 раз
e) Увеличится на 8
Обоснование: Определение. Умножением натуральных чисел называется алгебраическая операция, обладающая свойствами… &62, стр.243
Определение. Вычитанием натуральных чисел a и b называется операция, удовлетворяющая условию: a-b=c тогда и только тогда, когда b+c=a. &.64, с.249
Общий пример: а-b=c.
По условию мы уменьшаемое и вычитаемое увеличиваем в 4 раза и получаем: (а*4) – (b*4) = 4(а-b). Таким образом, мы видим, что разность увеличится в 4 раза.
Пример: 10-4=6; 40-16=24. И 24:6=4
46 Если число а при делении на 5 дает в остатке 1, то число а2 при делении на 5 дает в остатке
a) 0 c) 3 e) 1
b) 2 d) 4
Обоснование. По определению. Делением натуральных чисел а и b называется операция, удовлетворяющая условию: а:b=с тогда и только тогда, когда b*с=а &65, стр.251
Общий вид: Представим число а:5, если дает остаток 1, то имеет вид 5 k +1.
А2:5 можно записать как (5 k +1)2=252 k +5k+1
Мы видим, что первые 2 числа делятся на 5 без остатка, значит 1- и есть остаток.
47 В аксиоматической теории свойство антисимметричности отношения «меньше» доказывается
a) Методом от противного
b) С помощью дедуктивного вывода
c) Методом математической индукции
d) Методом полной индукции
e) На основе закона контрапозиции
Обоснование: &63. стр. 246, теорема 14. Если а <b , то b<a
48 В аксиоматической теории свойство транзитивности отношения «меньше» доказывается
a) С помощью дедуктивного вывода
b) Методом математической индукции
c) Методом от противного
d) Методом полной индукции
e) На основе закона контрапозиции
Обоснование: &63. стр. 246, теорема 13. Если а< b , и b < c , то а< c
49 При доказательстве того, что деление на нуль невозможно рассматривается
a) Два случая d) Несколько частных случаев
b) Один случай e) Другой ответ
c) Три случая
Обоснование:&66, стр. 254-255, Теорема 28. Деление на ноль невозможно. Рассматривается 2 случая, когда а не = 0 , и когда а=0.
50 Как называется число b в равенстве a : b = c
a) Вычитаемое c) Делитель e) Разность
b) Делимое d) Частное
Обоснование: Число а: b называется частным чисел a и b , число а-делимым, число b -делителем. &65 , стр.252
51 Как называется число а в равенстве 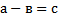
a) Уменьшаемое c) Вычитаемое e) Другой ответ
b) Делимое d) Разность
Обоснование: Число a - b - называются разностью чисел а и b , число а- уменьшаемым, а число b -вычитаемым. &64 , стр.249
52 Какое свойство неявно используют младшие школьники при выполнении задания 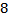
a) Коммутативное свойство сложения
b) Свойство монотонности сложения
c) Свойство сократимости сложения
d) Ассоциативное свойство сложения
e) Другой ответ
Обоснование: С отношением "меньше"("больше") для натуральных чисел младшие школьники знакомятся в самом начале обучения. И часто, наряду с его теоретико- множественной трактовкой, неявно используется определение, данное нами в рамках аксиоматической теории. Например, учащиеся могут объяснить , что 9> 7 , так как 9 - это 7+2. Нередко и неявное использование свойств монотонности сложения и умножения. Например, дети объясняют, что " 6+2< 6+3, так как 2 <3» &63 , стр.248
53 Первая аксиома Пеано формулируется так:
a) В множестве N существует элемент, непосредственно не следующий ни за каким элементом этого множества. Называют его единицей
b) Для каждого элемента а из N существует единственный элемент а´, непосредственно следующий за а.
c) Пусть множество М есть подмножество множества N и известно, что единица содержится в М; и из того, что а содержится в М, следует, что и а´ содержится в М. Тогда множество М совпадает с множеством N.
d) Прямая разделяет плоскость на две полуплоскости.
e) Для каждого элемента а из N существует не более одного элемента, за которым непосредственно следует а.
Обоснование: &60, стр. 233, 1 аксиома
54 Четвертая аксиома Пеано формулируется так:
a) Пусть множество М есть подмножество множества N и известно, что: единица содержится в М; и из того, что а содержится в М, следует, что и а´ содержится в М. Тогда множество М совпадает с множеством N.
b) Для каждого элемента а из N существует не более одного элемента, за которым непосредственно следует а.
c) Прямая разделяет плоскость на две полуплоскости.
d) В множестве N существует элемент, непосредственно не следующий ни за каким элементом этого множества. Называют его единицей.
e) Для каждого элемента а из N существует единственный элемент а´, непосредственно следующий за а.
Обоснование: &60, стр. 233, 4 аксиома
55 Используя определение умножения натуральных чисел в аксиоматической теории, найдите значение выражения 3*7
a) 3*7=3*(10-3)=3*10-3*3=30-9=21
b) 3*7=3+3+3+3+3+3+3=21
c) 3*7=7+7+7=21
d) 3*7=3*(5+2)=3*5+3*2=15+6=21
e) 3*7=3*6’=3*6+3=18+3=21








