Обоснование: Понятие множества является одним из основных понятий в математике и поэтому не определяется через другие. &1, стр.7
31 При делении на 7 чисел a и b получаются остатки 2 и 5. тогда произведение ab при делении на 7 дает остаток:
a) 10 c) 2 e) 7
b) 3 d) 5
Обоснование: Решение основано на определении. Пусть а-целое неотрицательное число, а b – число натуральное. Разделить а на b остатком – это значит найти такие целые неотрицательные числа q и r , что a = bq + r , причем 0 ≤ r < b &66, стр.255
Числа можно представить так: первое: (7a+2) И второе :(7b+5), а и b принадлежат N
7a и 7b - целая часть чисел, которая делится на 7, а 2 и 5 – являются остатками. Тогда их произведение (7a+2)(7b+5) = 49ab + 35a + 14b + 10. Из получившегося выражения видим, что первые три слагаемых делятся на 7 без остатка ,когда а и b принадлежат N .
Остается число 10, которое не целиком делится на 7, а дает остаток 3 . Таким образом, при делении произведения этих чисел остаток будет равен 3.
32 Не выполняя вычислений выясните значения каких выражений будут равны
a) (50+16)-14 и 50+(16-14)
b) (50+16)-14 и 50-(16-14)
c) (50+16)-14 и (50-16)+14
d) (50+16)-14 и (50-14)-16
e) (50+16)-14 и 50-(16+14)
Обоснование: &64, стр. 250 , теорема 21 б) если b > c , то ( a + b )- c = a +( b -c) . Для того чтобы вычесть число из суммы, достаточно вычесть это число из одного слагаемого суммы и к полученному результату прибавить другое слагаемое.
33 Если из системы аксиом нельзя логически вывести два взаимно исключающих друг друга предложения, то она называется:
a) полной
b) независимой
c) непротиворечивой
d) противоречивой
e) зависимой
Обоснование: Система аксиом называется непротиворечивой, если из нее нельзя логически вывести два взаимно исключающих друг друга предложения. &59 , стр.232
34 Отрезком Na натурального ряда называется
a) множество натуральных чисел, в котором а элементов
b) конечное множество А, где 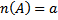
c) множество последовательных натуральных чисел, в котором а элементов
d) множество натуральных чисел, не превосходящих натурального числа а
e) другой ответ
Обоснование: Определение. Отрезком Na натурального ряда называется множество натуральных чисел, не превосходящих натурального числа а. &68, стр.259
35 Если с и d- натуральные числа, то 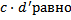
a) 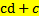 c)
c) 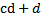 e)
e) 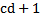
b) 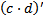 d)
d) 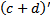
Обоснование: Умножением натуральных чисел называется алгебраическая операция, которая обладает этим свойством. ( A , b принадлежат N ) a * b ’ = a * b + a &62, стр.243, 2 свойство
36 Множества А и В называют равномощными, если
a) 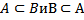
b) Если каждому элементу множества А соответствует элемент множества В
c) Если они равночисленны
d) Между ними можно установить взаимно-однозначное соответствие
e) Другой ответ








