Обоснование: Если a < b и b < c , то а<с . Это теорема выражает свойство транзитивности отношения «меньше» &63, стр.246, теорема 13
22 Если при делении с остатком числа а на 15 получили неполное частное 10, то наибольшее возможное значение делимого:
a) 150 d) 165
b) 160 e)151
c) 164
Обоснование: Решение основано на определении. Пусть а-целое неотрицательное число, а b – число натуральное. Разделить а на b остатком – это значит найти такие целые неотрицательные числа q и r , что a = bq + r , причем 0 ≤ r < b &66, стр.255
Найдем наибольшее значение делимого а, если b=15, q=10, а остаток r находится в промежутке 0≤r<15, значит, наибольший остаток 14, отсюда следует: а=15*10+14=164
23 Законы сложения натуральных чисел в аксиоматической теории доказываются:
a) методом от противного
b) методом полной индукции
c) с использованием дедуктивного вывода
d) методом математической индукции
e) другой ответ
Обоснование: &67, стр.257 Теорема 30, метод, основанный на этой теореме называется методом математической индукции. Данный метод доказательства можно использовать при доказательстве свойств сложения и умножения, и применять при сложении натуральных чисел.
24 Если А(1) и (А(k) => А(k+1)) – истинное высказывание, то делают вывод о том, что утверждение А (n) истинно для любого натурального числа n. Так формулируется:
a) дедуктивный вывод
b) метод математической индукции
c) метод полной индукции
d) закон контрапозиции
e) другой ответ
Обоснование: &67, стр.257 Теорема 30, метод, основанный на этой теореме называется методом математической индукции
25 Если делимое и делитель умножить на n, то частное:
a) увеличится в n раз
b) не изменится
c) уменьшится в n раз
d) увеличится на n
e) уменьшится на n
Обоснование:Из определения. Делением натуральных чисел a и b называется операция, удовлетворяющая условию: a : b = c тогда и только тогда, когда b * c = a &65, стр.251
Если мы делимое и делить умножим на одно и тоже чисто, то частное не изменится. Общий вид: a : b = c , если мы умножим на одно и тоже значение k , то получим: (а* k ):( b * k )= c * k , мы видим, что число k остается неизменным и его можно сократить и получается первоначальное равенство a : b = c . Например: 10:5=2 и 20:10=2
26 Метод математической индукции состоит:
a) из четырех частей
b) из одной части
c) из пяти частей
d) из двух частей
e) из n частей
Обоснование: Метод математической индукции состоит из двух частей &67,стр.257
27 Деление является алгебраической операцией на множестве:
a) натуральных чисел
b) целых неотрицательных чисел
c) целых чисел
d) иррациональных чисел
e) рациональных чисел
Обоснование: Рациональные числа – это числа, которые можно записать в виде положительной обыкновенной дроби, отрицательной обыкновенной дроби или числа нуль. Операция деление является алгебраической на множестве рациональных чисел. Лекция 1 в тетради
28 Множество натуральных чисел – упорядоченное множество, так как отношение «меньше» для натуральных чисел:
a) транзитивно и симметрично
b) является отношением эквивалентности
c) рефлексивно и симметрично
d) рефлексивно и транзитивно
e) транзитивно и антисимметрично
Обоснование: Отношение «меньше» антисимметрично и транзитивно и обладает свойством связанности, то оно является отношением линейного порядка, а множество натуральных чисел – линейно упорядоченным множеством &63, стр.247
29 Разность натуральных чисел а-b существует только тогда, когда
a)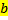 
<a c) 
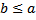e) другой ответ
b)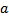 
<b d)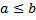 
Обоснование: Разность натуральных чисел a и b c уществует тогда и только тогда, когда b < a По теореме 19 &64, стр.249
30 Одним из основных (неопределяемых) понятий математики является:
a) теорема
b) квадрат
c) умозаключение
d) индукция
e) множество