Обоснование: &64, стр.250, теорема 22. Для того чтобы вычесть из числа сумму чисел, достаточно вычесть из этого числа последовательно каждое слагаемое одно за другим.
15 Чтобы узнать, на сколько одно число меньше или больше другого, надо:
a) из большего числа вычесть меньшее
b) к большему числу прибавить меньшее
c) большее число разделить на меньшее
d) меньшее число умножить на какое-нибудь натуральное число
e) большее число умножить на меньшее
Обоснование: &64, стр.249, теорема 19
16 Запишите, используя символику, правый дистрибутивный закон умножения относительно сложения для натуральных чисел:
a) 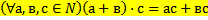
b) 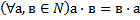
c) 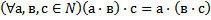
d) 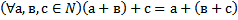
e) 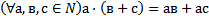
Обоснование: &62 , стр.244, теорема 8
1 При делении целых неотрицательных чисел на число 7 могут получиться остатки:
f) 1, 2, 3, 4, 5, 6, 7
g) 0, 1, 2, 3, 4, 5, 6
h) 1, 2, 3
i) 1, 3, 5, 7
j) 0, 1, 2, 3, 4, 5, 6, 7
Обоснование: Определение. Пусть а-целое неотрицательное число, а b – число натуральное. Разделить а на b остатком – это значит найти такие целые неотрицательные числа q и r , что a = bq + r , причем 0 ≤ r < b &66, стр.255
17 Как изменится сумма двух натуральных чисел, если каждое из двух слагаемых увеличить в 2 раза
a) Увеличится в 4 раза
b) Увеличится на 2 раза
c) Увеличится на 4 раза
d) Увеличится в 2 раза
e) Другой ответ
Обоснование: &62 , стр.244, теорема 8
Пример: было a + b = c , умножим на 2 и получим : ( a + b )*2= a *2+ b *2=с , т.е получим 2с , следовательно увеличится в 2 раза
18 Число а при делении на 8 дает в остатке 3 и поэтому имеет вид:
a) 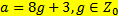
b) 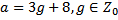
c) 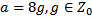
d) 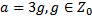
e) 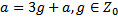
Обоснование: Определение. Пусть а-целое неотрицательное число, а b – число натуральное. Разделить а на b остатком – это значит найти такие целые неотрицательные числа q и r , что a = bq + r , причем 0 ≤ r < b &66, стр.255
19 Для того, чтобы существовало частное двух натуральных чисел a и b , необходимо, чтобы
a) 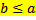
b) 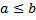
c) 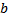
d) 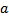
e) другой ответ
Обоснование: Для того чтобы существовало частное двух натуральных чисел а и b , необходимо чтобы b ≤ a &65, стр.252, теорема 23
20 Множество N при помощи отношения «иметь один и тот же остаток при делении на 6» разбивается на
a) 5 классов
b) 2 класса
c) 6 классов
d) 3 класса
e) другой ответ
Обоснование: Определение. Пусть а-целое неотрицательное число, а b – число натуральное. Разделить а на b остатком – это значит найти такие целые неотрицательные числа q и r , что a = bq + r , причем 0 ≤ r < b &66, стр.255
Следовательно при делении на 6 может остаться 6 остатков:0,1,2,3,4,5,6 и их получается 6, следовательно, 6 классов
21 Свойство транзитивности отношения «меньше» на множестве натуральных чисел записывается так:
a) Для любых натуральных чисел a,b,c, если a<b и b<c, то a<c
b) Для любых натуральных чисел a,b, если a<b, то неверно, что в<а
c) Для любых натуральных чисел a, неверно, что a<a
d) Для любых натуральных чисел a,b, a<b или b<a
e) Для любых натуральных чисел a,b, если a<b, то b<a








