Обоснование: По формулировке Аксиома- предложения, которые в данной теории принимаются без доказательства; в них раскрываются свойства основных понятий. &59 , стр.232
,ТЕМА 1
АКСИОМАТИЧЕСКОЕ ПОСТРОЕНИЕ СИСТЕМЫ
НАТУРАЛЬНЫХ ЧИСЕЛ
Цель: Проверить знание понятий данной темы (аксиоматическое определение системы натуральных чисел, число как элемент натурального ряда), отношения «меньше», четырех арифметических действий, отрезка натурального ряда, конечного множества, числа элементов множества, счета, применять знания и умения для решения практических задач.
Задания к тестам: выделить желтым цветом правильные ответы; дать обоснование правильных ответов. В обосновании сформулировать в теоретических заданиях определение, теорему, указать номер теоремы, пункт и стр. учебника, в практических решение, используя метод. рекоменд. К контрольной работе. Обоснование дать к каждому тестовому заданию.
Ф.И.О. Фарапонова Екатерина Алексеевна
Группа: ОБ-РНО-11
1 Утверждения, которые принимаются без доказательства,
называются:
a) определениями
b) теоремами
c) аксиомами
d) примерами
e) высказываниями
Обоснование: По формулировке Аксиома- предложения, которые в данной теории принимаются без доказательства; в них раскрываются свойства основных понятий. &59 , стр.232
2 Требования, предъявляемые к системе аксиом:
a) полнота, монотонность, независимость
b) непротиворечивость, независимость, полнота
c) независимость, непротиворечивость, монотонность
d) монотонность, полнота, непротиворечивость
e) полнота, монотонность, противоречивость
Обоснование: К системе аксиом предъявляются особые требования. Прежде всего она должна быть непротиворечивой и независимой. &59 , стр.232
3 При аксиоматическом построении системы натуральных чисел элемент, непосредственно следующий за элементом а обозначают:
a) – а
b) 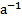
c) а,
d) 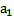
e) - 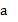
Обоснование: Элемент, непосредственно следующий за элементом а, обозначают а, . &60 , стр.233
4 Система аксиом Пеано содержит:
a) 2 аксиомы
b) 5 аксиом
c) 3 аксиомы
d) 4 аксиомы
e) 6 аксиом
Обоснование: Сформулированные 4 аксиомы часто называют аксиомами Пеано. &60 , стр.233
5 Элементы множества N , для которых установлено отношение «непосредственно следовать за», удовлетворяющие четырем аксиомам Пеано, называются:
a) четными числами
b) нечетными числами
c) положительными числами
d) натуральными числами
e) другой ответ
Обоснование: из определения: Множество N , для элементов которого установлено отношение «непосредственно следовать за» , удовлетворяющее аксиомам 1-4, называется множеством натуральных чисел , а его элементы – натуральными числами. &60, стр. 233
6 Термин «натуральное число» впервые употребил:
a) Евклид
b) Архимед
c) Пифагор
d) Фалес
e) Боэций
Обоснование: Термин «натуральное число» впервые употребил в 5в. Римский ученый А.Боэций, который известен как переводчик работ известных математиков прошлого на латинский язык как автор книги «О введении в арифметику», которая до XVI века была образцом для всей европейской математики. &13, стр.231
7 Науку, в которой изучаются натуральные числа и действия над ними, называют:
a) алгебра
b) арифметика
c) математика
d) геометрия
e) натурология
Обоснование: Теоретическая наука, которая стала изучать числа и действия над ними, получила название «арифметика». От греческого слова означает «число». &13 , стр.230
8 Для счета предметов достаточно множества:
a) целых чисел
b) рациональных чисел
c) иррациональных чисел
d) действительных чисел
e) натуральных чисел
Обоснование: Чтобы вести счет, нужна последовательность числительных, которая начинается с единицы и которая позволяет осуществлять переход от одного числительного к другому и столько раз, сколько это необходимо. Нужен отрезок натурального ряда. &14, стр.231
9 Ассоциативный закон сложения натуральных чисел выглядит так:
a) 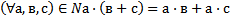
b) 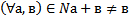
c) 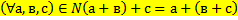
d) 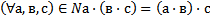
e) 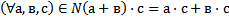
Обоснование: & 61, стр.240, теорема 4
10 Действие, с помощью которого находят разность натуральных чисел, называют:
a) уменьшение
b) сложение
c) вычитание
d) деление
e) уменьшаемое
Обоснование: Определение. Вычитанием натуральных чисел а и b называется операция, удовлетворяющая условию: a - b = c тогда и только тогда, когда b + c = a , & 64 стр. 249
11 Числа при умножении называются:
a) слагаемые
b) множители
c) делители
d) делимые
e) уменьшаемые
Обоснование: Число a*b называется произведением чисел a и b, а сами числа a и b – множителями. &62, стр.243
12 Действие, при помощи которого находят частное натуральных чисел называют:
a) умножением
b) сложением
c) вычитанием
d) делением
e) разностью
Обоснование: Из определения. Делением натуральных чисел а и b называется операция, удовлетворяющая условию: a : b = c тогда и только тогда , когда b * c = a , &65, стр.251
13 Если к множеству натуральных чисел добавить нуль, то получится новое множество, которое называют множеством :
a) целых отрицательных чисел
b) целых положительных чисел
c) множеством положительных чисел
d) целых неотрицательных чисел
e) другой вариант ответа
Обоснование: Присоединим к множеству N натуральных чисел еще один элемент, который называется нулем 0. Полученное множество называется множеством целых неотрицательных чисел и обозначается Z 0 . Таким образом, Z 0 = N и {0} , &66, стр.254
14 Для того чтобы вычесть сумму из числа, достаточно вычесть из этого числа каждое слагаемое последовательно одно за другим. Это правило:
a) деления разности на число
b) деления суммы на число
c) вычитания числа из суммы
d) вычитания разности из числа
e) вычитания суммы из числа








