Свойства пересечения и объединения множеств
1) Коммутативное свойство (переместительное):
Для любых множеств А и В выполняются равенства:
А 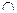 В = В
В = В 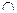 А
А
А 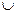 В = В
В = В 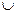 А
А
2) Ассоциативное свойство (сочетательное):
Для любых множеств А и В выполняются равенства:
(А 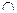 В)
В) 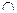 С = А
С = А 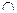 (В
(В 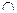 С)
С)
(А 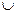 В)
В) 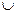 С = А
С = А 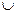 (В
(В 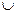 С)
С)
3) Дистрибутивное свойство (распределительное):
Для любых множеств А и В выполняются равенства:
(А 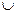 В)
В) 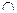 С = (А
С = (А 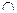 С)
С) 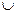 (В
(В 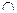 С)
С)
(А 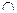 В)
В) 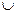 С = (А
С = (А 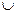 С)
С) 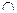 (В
(В 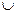 С)
С)
Замечание:
Если нет скобок, то сначала выполняют пересечение, а затем объединение ( 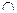 более «сильная» операция, чем
более «сильная» операция, чем 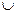 ).
).
 А В
А В
Задание 25
Проиллюстрируйте ассоциативное (сочетательное) свойство
пересечения и объединения множеств, используя круги Эйлера (рис. 35).
С
Рис. 35
Можно находить разность множеств.
Разностью множеств А и В называется множество А\В, содержащее только те элементы, которые принадлежат множеству А и не принадлежат множеству В.
А\В = {х | х Î А и х 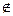 В }
В }
Рассмотрим примеры, используя рисунок 30.
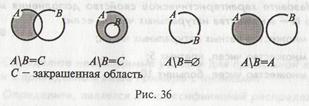
1) Пусть А – множество треугольников, В – множество черных фигур, С – множество белых треугольников. Тогда множество С можно рассматривать как разность множеств А и В, так как белые треугольники принадлежат множеству А и не принадлежат множеству В: А\В=С.
2) Пусть А – множество изображенных треугольников, В – множество изображенных черных треугольников, С – множество изображенных белых треугольников. Так как множество В является подмножеством множества А, то оставшаяся часть множества А, то есть белые треугольники (множество С), и будет разностью: А\В=С.
3) Пусть А множество изображенных квадратов, В – множество изображенных четырехугольников. Так как эти множества равны, то разностью множества А и В будет пустое множество: А\В=Ø.
4) Пусть А – множество изображенных треугольников, В – множество изображенных квадратов. У этих множеств нет общих элементов, то есть ни один элемент множества А не принадлежит множеству В, поэтому разностью множеств А и В будет множество А: А\В=А.
Разность двух множеств можно изобразить при помощи кругов Эйлера (рис. 36).
В работе с детьми чаще всего рассматривается второй случай, когда одно множество является подмножеством другого. Он учит выделять часть из множества, определяя оставшуюся часть. Это используется и для изучения действия вычитания чисел. Например, решая задачу: «В корзине лежало 7 огурцов, 2 из них съели. Сколько осталось?», выделяют три множества (первоначальное множество огурцов в корзине, множество съеденных огурцов, множество оставшихся огурцов):
· Сколько было огурцов в корзине? (7)
· Сколько съели огурцов? (2)
· Сколько осталось огурцов в корзине? (5)
· Как получилось число 5? (7 – 2 = 5).
Из исходного множества ребенок удаляет подмножество и считает количество элементов в оставшемся множестве. В данном случае разность множеств называется дополнением.
Если множество В является подмножеством множества А, то дополнением множества В до множества А называется множество, содержащее только те элементы множества А, которые не принадлежат множеству В:
Если В 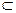 А, то В´
А, то В´ 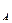 = {х | х Î А и х
= {х | х Î А и х 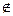 В}
В}
Замечание:
А\В 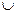 С – разность и объединение считают равноправными и выполняют по порядку в случае отсутствия скобок.
С – разность и объединение считают равноправными и выполняют по порядку в случае отсутствия скобок.
А\В 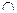 С – сначала выполняют пересечение, как более «сильное» действие.
С – сначала выполняют пересечение, как более «сильное» действие.
Задание 26
1. Перечислите элементы дополнения множества летних месяцев до множества месяцев года.
2. Назовите характеристическое свойство дополнения множества А до N – множества натуральных чисел, если:
А – множество четных натуральных чисел;
А – множество чисел, кратных 5;
А – множество чисел, больших 10.








