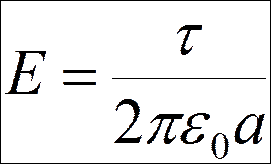Электростатическое поле – центральное поле сил Þ оно потенциально.

Дата: 2025-06-02; Просмотры: 10
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Работа его сил по перемещению заряженной частицы не зависит от траектории, а определяется лишь начальным и конечным положением частицы. Эта работа может быть представлена как разность потенциальных энергий.

Потенциал - это энергетическая

характеристика поля, это скалярная

физическая величина, численно равная потенциальной энергии, которой

обладает единичный положительный

заряд, помещенный в данную точку поля:

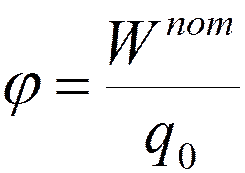
Потенциал поля точечного заряда:

.

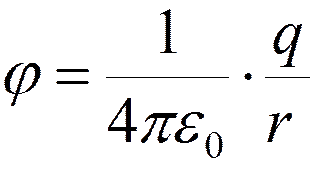Связь между напряженностью и потенциалом:

.

;

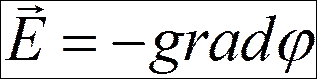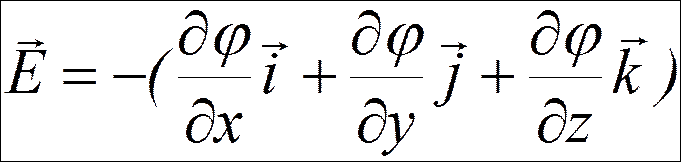Проекции вектора напряженности

;

;

;

:

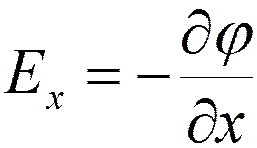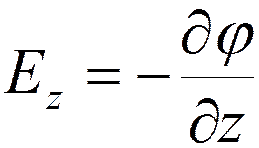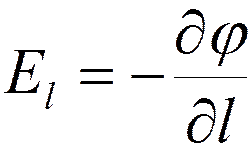
или

.

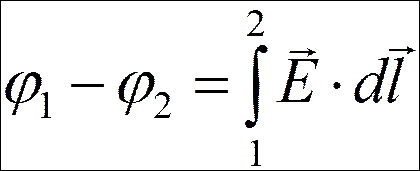В однородном поле ;

здесь h = l 12

1 СИ j =1 В

1 В = 1 СИЕ .1 м Þ 1 СИ E = 1 В /м

Любой заряд q , находящийся в эл. поле в точке, потенциал которой j , обладает потенциальной энергией

.

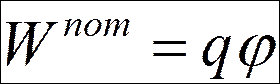Работа сил электростатического поля по перемещению заряда q из данной точки в бесконечность

.

Потенциальная энергия взаимодействия точечных зарядов q 1 и q 2 , находящихся на расстоянии r друг от друга:

.

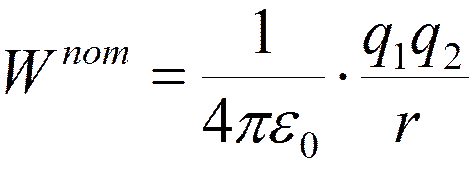Работа сил электростатического поля по перемещению заряда q из точки 1 в точку 2

.

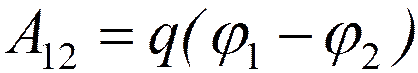Пусть (.)1 ® (.)2, тогда ( j 1- j 2) ® 0,

А12 ® 0

-

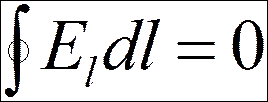- теорема о циркуляции напряженности электростатического поля или условие потенциальности электростатических полей.

Если поле создано системой зарядов, потенциал его определяется алгебраической суммой потенциалов полей, созданных каждым зарядом в отдельности (принцип суперпозиции):

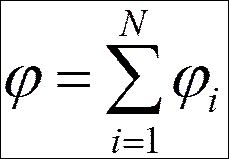
При графическом изображении полей кроме силовых линий изображают эквипотенциальные поверхности, т.е. поверхности равного потенциала

Уравнение эквипотенциальной поверхности j ( x , e , z ) = 0

Линии напряженности в каждой точке ортогональны эквипотенциальным поверхностям



ЗАДАЧИ. Расчет электростатических полей методом суперпозиции.

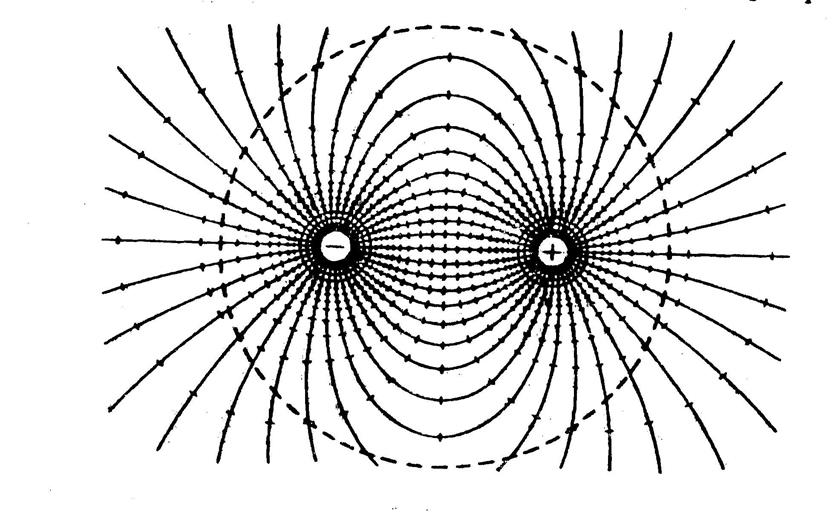
ЗАДАЧА 1. Расчет поля электрического диполя

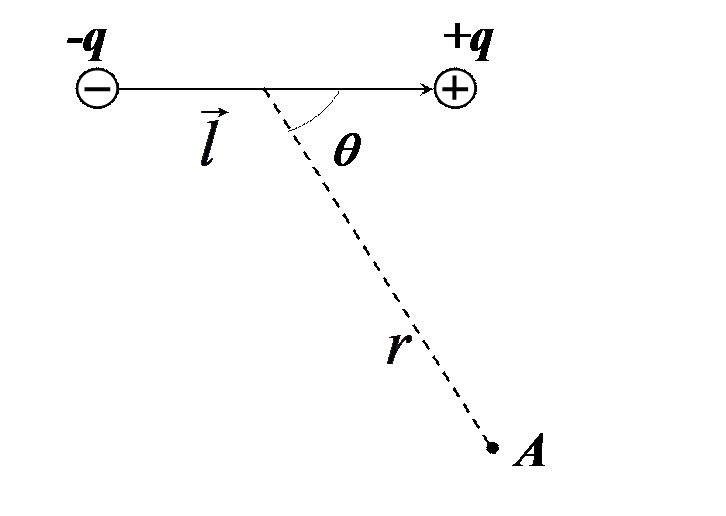
Электрическим диполем называется система двух одинаковых по абсолютной величине разноименных точечных зарядов + q и - q , расстояние l , между которыми значительно меньше расстояния до тех точек, в которых определяется поле системы.

Прямая, проходящая через оба заряда, называется осью диполя.

 

Электрический момент диполя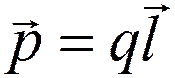

a ) точка А на оси диполя

 

;

;

;

;

.

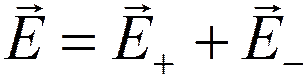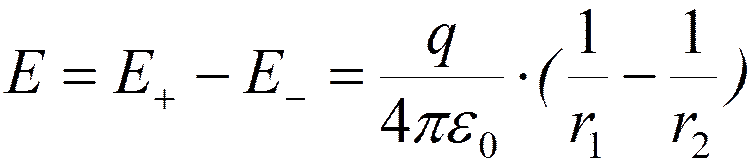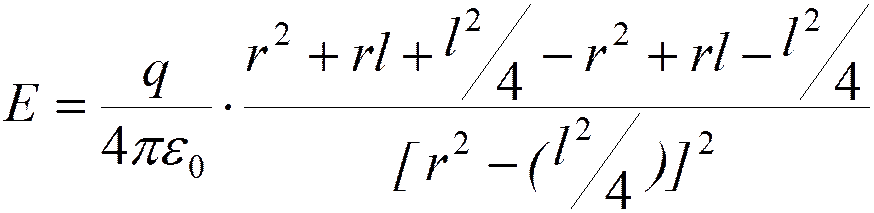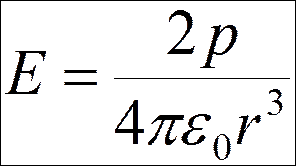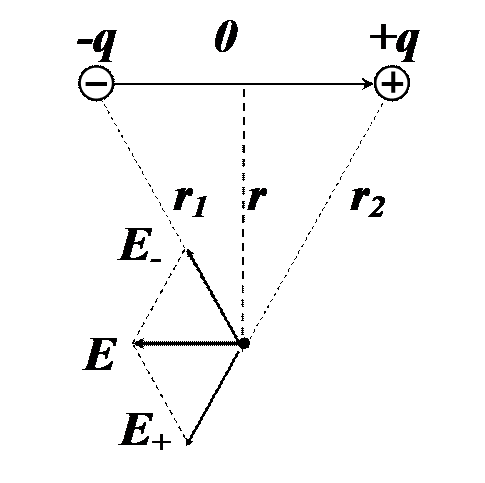б) точка А на прямой, перпендикулярной оси диполя

 
 

;

;

 

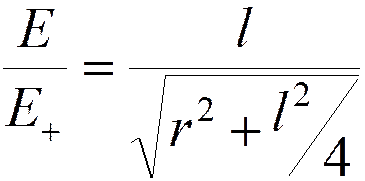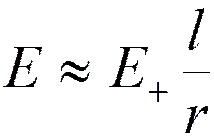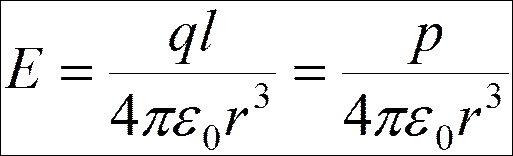
в) в общем случае

.

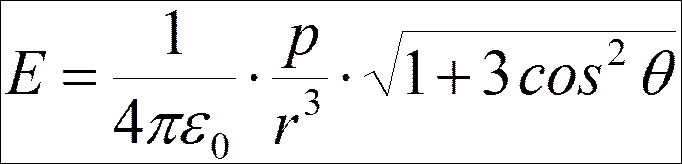ЗАДАЧА 2. Расчет поля заряженного отрезка

 

Найдем напряженность в точке А, расположенной на перпендикуляре, восстановленном к середине заряженного отрезка

Обозначим

ОА=а;

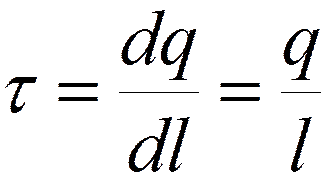- линейная плотность заряда

1 СИ t = 1 Кл/м

;

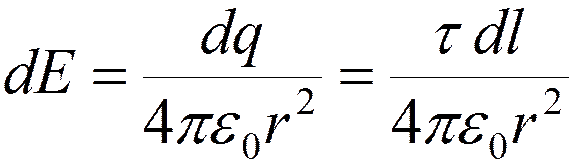
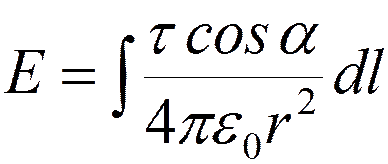
Перейдем к одной переменной ( a ):

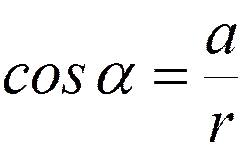Þ ;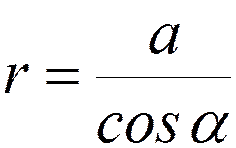

;

;

;

;

;

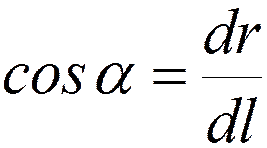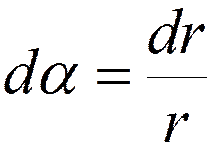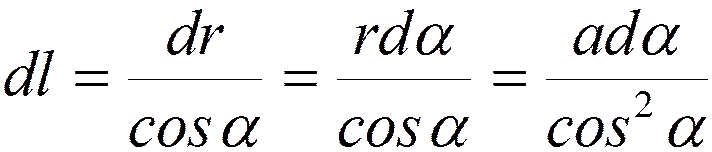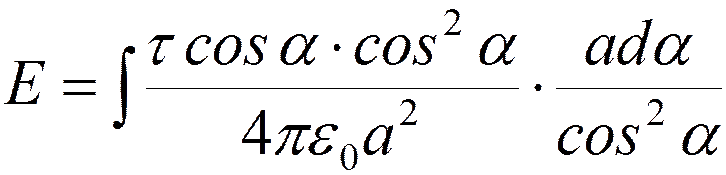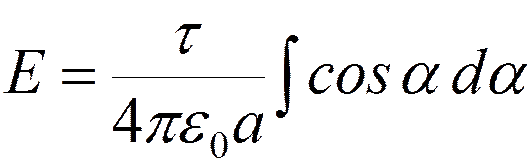
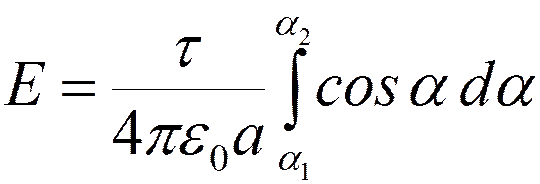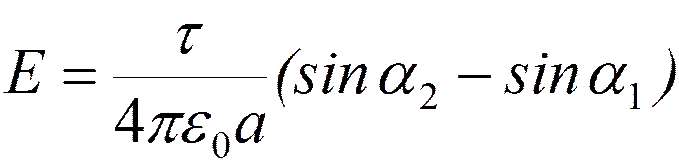
| a 1 | = | a 2 | = a м

(sin a 2 - sin a 1 ) = 2 sin a м

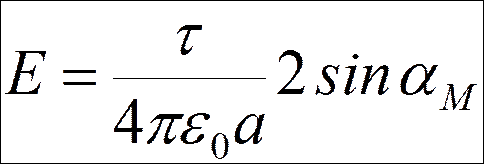
Для бесконечной заряженной нити

a 1 ® - p ¤ 2 ; a 2 ® + p ¤ 2 ;

(sin a 2 - sin a 1 ) ® 2;