Підставивши значення і з останніх співвідношень у формулу (б), дістанемо . (в)
Підставимо числове значення 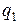 у (в) і знайдемо
у (в) і знайдемо
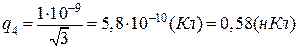 .
.
Відповідь: 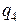 =0,58 нКл.
=0,58 нКл.
5.3. Точковий заряд 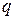 =25нКл знаходиться в електростатичному полі нескінченно довгого циліндра радіусом
=25нКл знаходиться в електростатичному полі нескінченно довгого циліндра радіусом 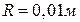 , який рівномірно
, який рівномірно
заряджений і має поверхневу густину заряду 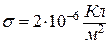 . Визначити силу
. Визначити силу
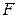 , що діє на заряд, якщо його відстань від осі циліндра
, що діє на заряд, якщо його відстань від осі циліндра 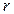 = 0,1м.
= 0,1м.

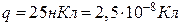 Розв’язування.
Розв’язування.
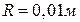 Абсолютне значення сили, що діє на точковий
Абсолютне значення сили, що діє на точковий 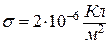 заряд
заряд 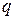 , який знаходиться в електростатичному
, який знаходиться в електростатичному
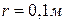 полі, визначають за формулою
полі, визначають за формулою

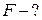
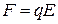 , (а)
, (а)
де 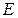 - абсолютне значення напруженості електростатичного поля. Напруженість поля нескінченно довгого рівномірно зарядженого циліндра
- абсолютне значення напруженості електростатичного поля. Напруженість поля нескінченно довгого рівномірно зарядженого циліндра
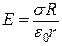 . (б)
. (б)
Підставивши значення Е з (б) у (а), знайдемо робочу формулу
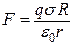 . (в)
. (в)
Підставимо у (в) числові значення фізичних величин і знайдемо значення
сили, що діє на заряд:
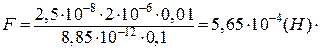
Відповідь: F =5,65 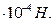
5.4 . Плоский диск радіусом R=0.1м заряджений позитивно. Заряд розподілений по його поверхні зі сталою густиною 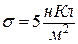 . Визначити потенціал електростатичного поля в точці М на осі симетрії, віддаленій від центра диска на 0,5м.
. Визначити потенціал електростатичного поля в точці М на осі симетрії, віддаленій від центра диска на 0,5м.

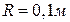 Розв’язування.
Розв’язування.
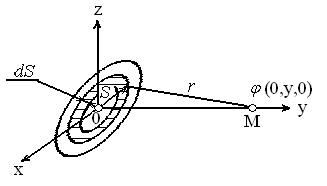
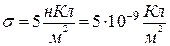 Розмістимо диск так, щоб вісь симетрії збігалася з
Розмістимо диск так, щоб вісь симетрії збігалася з 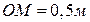 віссю Y прямокутної системи координат (рис.5.3).
віссю Y прямокутної системи координат (рис.5.3).

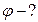 Виділимо на диску вузьке кільце. Якщо через S позначи-
Виділимо на диску вузьке кільце. Якщо через S позначи-
ти радіус цього кільця, а через 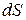 - його ширину, то площа кільця дорівнює
- його ширину, то площа кільця дорівнює 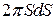 . Кількість електрики, що міститься на ньому, становитиме
. Кількість електрики, що міститься на ньому, становитиме 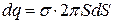 . Усі елементи заряду на вузькому кільці диска розміщені на однаковій відстані від точки М, а саме:
. Усі елементи заряду на вузькому кільці диска розміщені на однаковій відстані від точки М, а саме:
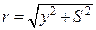 .
.

 Внесок кільцевої поверхн і в потенціал у точці М дорівнює
Внесок кільцевої поверхн і в потенціал у точці М дорівнює
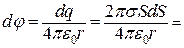
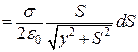 . (а)
. (а)
Рис.5.3 Щоб визначити потенціал,
зумовлений зарядженим диском, слід взяти інтеграл по всіх таких кільцях:
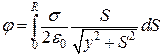 . (б)
. (б)
Зробимо таку підстановку змінних у виразі (б):
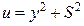 ;
; 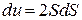 , звідки
, звідки 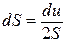 . (в)
. (в)
Замінимо у формулі (б) 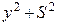 і
і 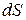 на їхні значения з виразу (в) і дістанемо:
на їхні значения з виразу (в) і дістанемо: 
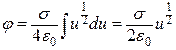
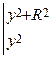
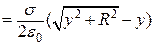 . (г)
. (г)
Підставимо числові значення в формулу (г):
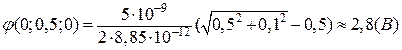 .
.
Відповідь: 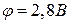 .
.
5.5. У вершинах правильного шестикутника із стороною а поміщають точкові заряди однакової величини 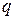 . Знайти потенціал
. Знайти потенціал 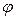 і напруженість Е поля в центрі шестикутника при умові, що:
і напруженість Е поля в центрі шестикутника при умові, що:
1 ) знак усіх зарядів однаковий,
2) знаки сусідніх зарядів протилежні.

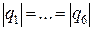 Розв’язування.
Розв’язування.
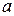 Згідно з принципом суперпозиції полів потенціал поля,
Згідно з принципом суперпозиції полів потенціал поля,

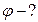 створеного системою зарядів, дорівнює алгебраїчній сумі
створеного системою зарядів, дорівнює алгебраїчній сумі
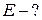 потенціалів, які утворені кожним із зарядів окремо. Врахувавши,
потенціалів, які утворені кожним із зарядів окремо. Врахувавши,
що 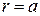 отримаємо:
отримаємо:
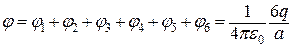 . (а)
. (а)
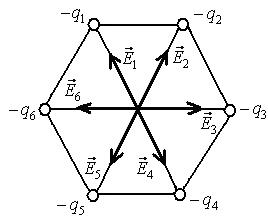
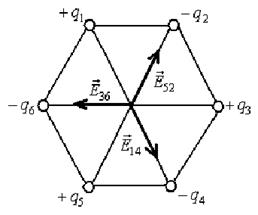
Рис.5.4 Рис.5.5
Напруженість поля системи зарядів дорівнює векторній сумі напруженостей полів, які створював би кожен із зарядів системи самостійно.
Напруженість поля кожного заряду 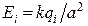 , тобто за величиною всі значення
, тобто за величиною всі значення 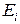 однакові. Внаслідок симетрії системи (рис.5.4):
однакові. Внаслідок симетрії системи (рис.5.4):
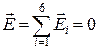 . (б)
. (б)
Міркуючи аналогічним чином, обчислимо потенціал поля у другому випадку:

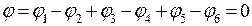 . (в)
. (в)
Напруженість поля 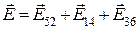 .Із рис.5.5 видно, що
.Із рис.5.5 видно, що 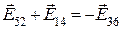 . Отже
. Отже
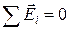 . (г)
. (г)
Відповідь: 1) 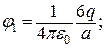
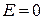
2) 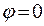 ,
, 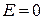 .
.
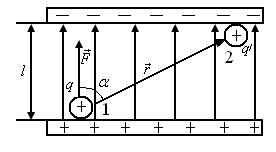
5.6. Знайти роботу 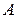 сил електростатичного поля по переміщенню заряду
сил електростатичного поля по переміщенню заряду 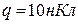 із точки 1 в точку 2 (рис.5.6), що знаходяться між двома різноймен- но зарядженими площинами, відстань
із точки 1 в точку 2 (рис.5.6), що знаходяться між двома різноймен- но зарядженими площинами, відстань 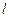 між якими дорівнює
між якими дорівнює 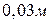 . Поверхнева густина заряду
. Поверхнева густина заряду 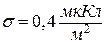 .
.

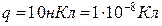 Розв’язування.
Розв’язування.
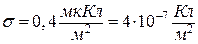 Можливі два способи розв’язування цієї задачі.
Можливі два способи розв’язування цієї задачі.

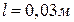 1-й спосіб. Роботу сил поля по переміщенню заряду
1-й спосіб. Роботу сил поля по переміщенню заряду
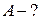 з точки поля з потенціалом
з точки поля з потенціалом 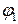 у точку з потенціалом
у точку з потенціалом
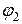 знайдемо за формулою:
знайдемо за формулою:
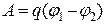 . (а)
. (а)
 Оскільки напруженість поля
Оскільки напруженість поля 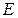 дорівнює градієнту потенціалу з протилежним знаком, то можна записати
дорівнює градієнту потенціалу з протилежним знаком, то можна записати
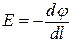 , (б)
, (б)
звідки
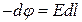 . (в)
. (в)
Проінтегруємо вираз (в), взявши до уваги, Рис.5.6 що поле між нескінченними паралельними
рівномірно різнойменно зарядженими площинами однорідне, його напруженість 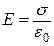 :
:
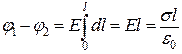 . (г)
. (г)
Підставивши у вираз (а) значення різниці потенціалів із залежності (г), знайдемо
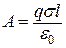 . (д)
. (д)
2-й спосіб. Оскільки поле між площинами однорідне, то сила, що діє на заряд 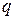 при його переміщенні, стала. Тому роботу сил поля по переміщенню заряду
при його переміщенні, стала. Тому роботу сил поля по переміщенню заряду 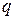 з точки 1 у точку 2 можна знайти за формулою
з точки 1 у точку 2 можна знайти за формулою
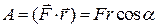 . (е)
. (е)
Врахувавши, що 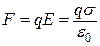 і
і 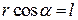 , знайдемо вираз для обчислення роботи:
, знайдемо вираз для обчислення роботи:
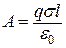 . (є)
. (є)
Отже, обидва способи розв’язування задачі дають один і той самий результат.
Знайдемо числове значення роботи:
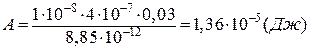 .
.
Відповідь: 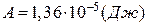 .
.
5.7. Знайти силу 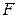 взаємодії двох молекул води, які знаходяться на відстані
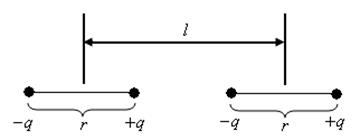
взаємодії двох молекул води, які знаходяться на відстані 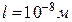 одна від одної (рис.5.7). Електричний дипольний момент молекули води
одна від одної (рис.5.7). Електричний дипольний момент молекули води 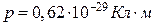 . Дипольні моменти молекул вважати розміщеними вздовж прямої, що з’єднує молекули.
. Дипольні моменти молекул вважати розміщеними вздовж прямої, що з’єднує молекули.
 Розв’язування.
Розв’язування.

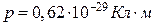
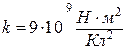

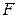 -?
-?
Рис.5.7
Розглянемо випадок, коли диполі лежать на одній прямій і орієнтовані один відносно одного протилежними зарядами, тобто дипольні моменти паралельні. Тоді, згідно з формулою (1.32) та законом Кулона, поле першого диполя діятиме на заряди 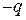 і
і 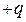 другого диполя відповідно з силами
другого диполя відповідно з силами
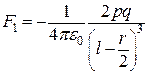 ,
, 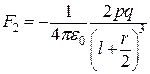 . (а)
. (а)
Оскільки сили 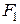 і
і 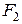 є антипаралельними, то їхня рівнодійна
є антипаралельними, то їхня рівнодійна
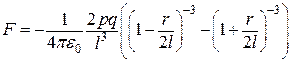 . (б)
. (б)
Враховуючи, що 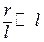 , і нехтуючи величинами вищих порядків малості, вираз (б) можна записати так:
, і нехтуючи величинами вищих порядків малості, вираз (б) можна записати так:
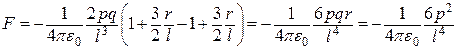 . (в)
. (в)
Виконавши обчислення, отримаємо:
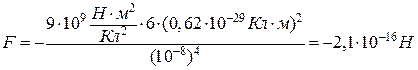 .
.
Знак мінус вказує на те, що диполі притягуються. При антипаралельному розміщенні дипольних моментів значення сили буде таке саме, але додатне, тобто диполі будуть відштовхуватись.
Відповідь: 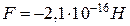 .
.
5.8. Диполь з електричним моментом 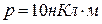 вільно встановився в однорідному електричному полі з напруженістю
вільно встановився в однорідному електричному полі з напруженістю 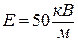 . Визначити зміну потенціальної енергії диполя у разі повороту його на
. Визначити зміну потенціальної енергії диполя у разі повороту його на 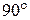 .
.

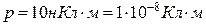 Розв’язування.
Розв’язування.
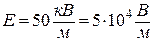 Вивести диполь зі стану стійкої рівноваги
Вивести диполь зі стану стійкої рівноваги
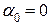 можна лише під дією зовнішніх сил. Тому, по-
можна лише під дією зовнішніх сил. Тому, по-
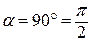 вертаючи диполь на певний кут
вертаючи диполь на певний кут 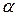 , зовнішні сили
, зовнішні сили
 виконуватимуть додатну роботу, яка витрачати-
виконуватимуть додатну роботу, яка витрачати-
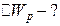 меться на зміну потенціальної енергії диполя:
меться на зміну потенціальної енергії диполя:
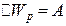 . (а)
. (а)
Елементарна робота 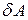 в разі повороту диполя на кут
в разі повороту диполя на кут 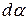 буде
буде
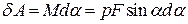 , (б)
, (б)
де 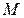 - момент пари сил
- момент пари сил 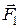 і
і 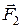 , що діють на заряди диполя з боку електричного поля.
, що діють на заряди диполя з боку електричного поля.
У разі повороту диполя від кута 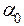 до кута
до кута 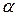 повна робота
повна робота
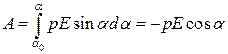
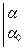 =
= 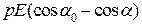 . (в)
. (в)
Величина роботи, виконаної зовнішніми силами, становитиме
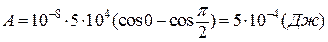 .
.
Згідно з виразом (а) зміна потенціальної енергії диполя
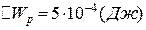 .
.
Відповідь: 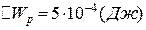 .
.
5.9. Відстані між центрами металевих кульок 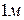 . Радіус кожної з них
. Радіус кожної з них 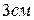 . Кульки відштовхуються з силою
. Кульки відштовхуються з силою 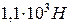 . Чому дорівнює поверхнева густина електричних зарядів кульок, якщо вони знаходяться в діелектрику з
. Чому дорівнює поверхнева густина електричних зарядів кульок, якщо вони знаходяться в діелектрику з 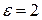 ?
?

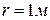 Розв’язування.
Розв’язування.
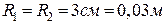 Оскільки кульки мають однакові радіуси і вони
Оскільки кульки мають однакові радіуси і вони 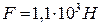 відштовхуються, то очевидно, що заряди кульок
відштовхуються, то очевидно, що заряди кульок

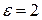 однакові за величиною й однойменні, тобто
однакові за величиною й однойменні, тобто 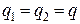 .
.
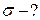 На поверхні кульок заряд розподілений рівномірно з
На поверхні кульок заряд розподілений рівномірно з
поверхневою густиною 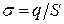 , звідки
, звідки
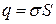 , (а)
, (а)
де 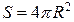 - площа поверхні кульки.
- площа поверхні кульки.
За законом Кулона сила взаємодії зарядів у діелектрику дорівнює
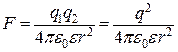 . (б)
. (б)
На підставі формул (а) і (б) отримуємо:
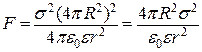 . (в)
. (в)
З рівняння (в) виведемо формулу для визначення 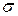 :
:
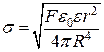 . (г)
. (г)
Знайдемо числове значення поверхневої густини електричних зарядів кульок
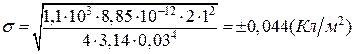 .
.
Відповідь: 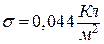 , якщо заряди кульок позитивні;
, якщо заряди кульок позитивні; 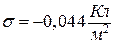 , якщо заряди кульок негативні.
, якщо заряди кульок негативні.
5.10. Конденсатори 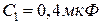 ,
, 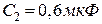 ,
, 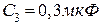 ,
, 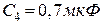 з’єднані так, як показано на рис.5.8. Різниця потенціалів між точками
з’єднані так, як показано на рис.5.8. Різниця потенціалів між точками 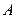 і
і 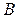 дорівнює
дорівнює  . Обчислити різницю потенціалів на кожному з конденсаторів і заряд на його обкладках.
. Обчислити різницю потенціалів на кожному з конденсаторів і заряд на його обкладках.
Розв’язування.

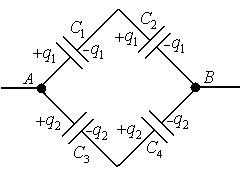
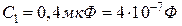 Як видно з рисунка,
Як видно з рисунка,
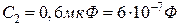 конденсатори
конденсатори 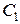 і
і 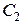
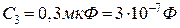 та
та 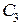 і
і 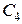 відповідно
відповідно
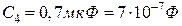 з’єднані послідовно в
з’єднані послідовно в
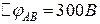 дві ланки, а ці ланки
дві ланки, а ці ланки
 з’єднані паралельно
з’єднані паралельно
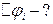 в точках
в точках 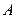 і
і 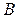 .
.
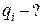 У разі послідовного
У разі послідовного
 Рис.5.8 з’єднання конденса-
Рис.5.8 з’єднання конденса-
торів заряд на всіх обкладках за абсолютною величиною буде однаковим.
Позначимо ці заряди на обкладках конденсаторів першої ланки 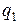 , а другої -
, а другої - 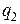 . Різниця потенціалів на першому конденсаторі
. Різниця потенціалів на першому конденсаторі 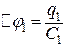 , на дру-
, на дру-
гому - 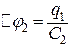 , на третьому -
, на третьому - 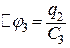 , на четвертому -
, на четвертому - 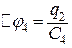 . Причому
. Причому
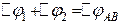 і
і 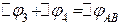 . Визначимо заряд
. Визначимо заряд 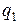 :
:
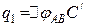 , (а)
, (а)
де 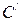 - електроємність першої ланки конденсаторів, сполучених послідовно. Знайдемо її:
- електроємність першої ланки конденсаторів, сполучених послідовно. Знайдемо її:
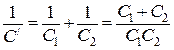 ,
,
звідки
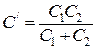 . (б)
. (б)
Підставимо 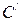 із (б) у вираз (а) й отримаємо:
із (б) у вираз (а) й отримаємо:
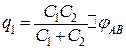 . (в)
. (в)
Аналогічно знайдемо, що
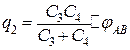 . (г)
. (г)
Тоді
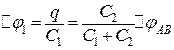 ;
; 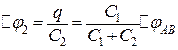 ;
;
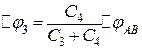 ;
; 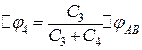 .
.
Обчислимо їх значення:
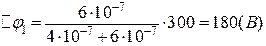 ;
; 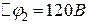 ;
; 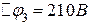 ;
; 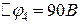 .
.
Заряди на пластинках конденсатора можна знаходити або за формулами (в) і (г), або за формулами різниці потенціалів між обкладками на одному з конденсаторів, взятому з першої та другої ланок. Так,
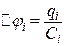 ,
,
звідки
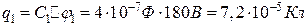 ;
;
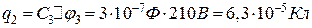 .
.
Відповідь: 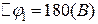 ;
; 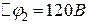 ;
; 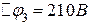 ;
; 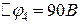 ;
; 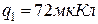 ;
; 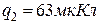 .
.
5.11. Відстань між обкладками плоского конденсатора 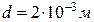 , різниця потенціалів
, різниця потенціалів 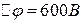 . Заряд кожної обкладки
. Заряд кожної обкладки 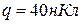 . Визначити енергію електричного поля конденсатора і силу взаємного притягання обкладок.
. Визначити енергію електричного поля конденсатора і силу взаємного притягання обкладок.

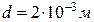 Розв’язування.
Розв’язування.
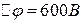 Енергія електричного поля плоского конденсатора:
Енергія електричного поля плоского конденсатора:
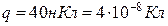
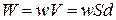 , (а)
, (а)

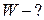 де
де 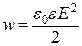 -об’ємна густина енергії електричного
-об’ємна густина енергії електричного
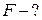 поля,
поля, 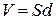 - об’єм конденсатора. Підставимо у
- об’єм конденсатора. Підставимо у
формулу (а) вираз для визначення 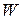 :
:
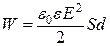 . (б)
. (б)
Електричне поле плоского конденсатора однорідне, тому його напруженість 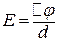 . Підставимо цей вираз у (б) і зробимо перетворення:
. Підставимо цей вираз у (б) і зробимо перетворення:
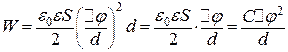 . (в)
. (в)
Оскільки відомий заряд на обкладках, то електроємність знайдемо через заряд і різницю потенціалів 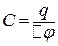 . Підставимо цей вираз С у формулу (в):
. Підставимо цей вираз С у формулу (в):
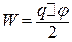 . (г)
. (г)
Обчислимо
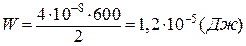 .
.
Для того, щоб розвести обкладки конденсатора на відстань 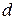 , необхідно виконати роботу проти сил протягування
, необхідно виконати роботу проти сил протягування 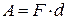 . Ця робота витрачається на зміни енергії конденсатора:
. Ця робота витрачається на зміни енергії конденсатора: 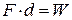 . Отже
. Отже
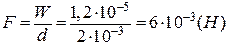 .
.
Відповідь: 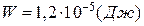 ;
; 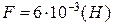 .
.
5.12. Електричне поле створено провідною зарядженою ( 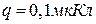 ) кулею радіусом
) кулею радіусом 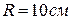 . Яка енергія
. Яка енергія 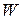 поля зосереджена в об’ємі, обмеженому кулею і концентричною з нею сферичною поверхнею, радіус якої вдвічі більший радіуса кулі?
поля зосереджена в об’ємі, обмеженому кулею і концентричною з нею сферичною поверхнею, радіус якої вдвічі більший радіуса кулі?

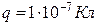 Розв’язування.
Розв’язування.
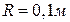 Оскільки куля провідна, то заряд
Оскільки куля провідна, то заряд 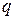 розподілиться по її
розподілиться по її
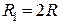 поверхні і в об’ємі кулі поле відсутнє. На поверхні кулі і за її
поверхні і в об’ємі кулі поле відсутнє. На поверхні кулі і за її

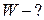 межами заряд кулі можна вважати точковим. Напруженість
межами заряд кулі можна вважати точковим. Напруженість
поля, створеного зарядом 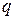 в точці на відстані
в точці на відстані 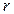 від центра кулі (рис.5.9)
від центра кулі (рис.5.9)
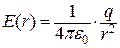 .
.
Енергія електричного поля у заданому об’ємі дорівнює:
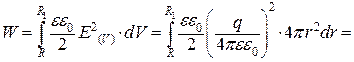
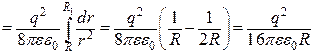 (а)
(а)
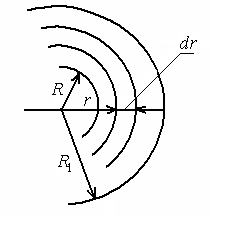
Враховуючи задані величини, на підставі формули (а) отримуємо:
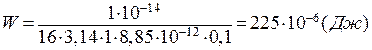 .
.
Відповідь: 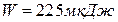 .
.
Рис.5.9
6. Задачі для самостійного розв’язування
1. Два точкові однойменні заряди по 30 мкКл кожен перебувають на відстані 20 см один від одного. Визначити величину та напрям сили, з якою ці заряди будуть діяти на позитивний заряд 20 нКл, розміщений на відстані 20 см від кожного з них.
2. Два позитивні заряди 0,3 та 0,2 мкКл перебувають на відстані 10 см один від одного. Де треба розмістити між ними третій заряд, щоб він перебував у рівновазі?
3. Точковий заряд 1 мкКл перебуває на деякій відстані поблизу пластини. Визначити поверхневу густину заряду пластини, якщо на точковий заряд діє сила 60 мН.
4. Дві однакові круглі пластини площею по 100 см2 кожна розташовані паралельно одна одній. Заряд однієї пластини – 10 мкКл, другої – 10 мкКл. Визначити силу взаємного притягання пластин, якщо відстань між ними 2 см.
5. Дві кульки, кожна масою 10 мг, підвішені на нитках довжиною по 50 см так, що їх поверхні торкаються. Після того як кулькам був наданий однаковий заряд, вони відійшли одна від одної на відстані 7 см. Знайти величину заряду кожної кульки.
6. Між двома вертикальними плоско паралельними пластинами, що перебувають на відстані 2 см одна від одної, підвішена заряджена кулька масою 0,1 г. При різниці потенціалів між пластинами 900 В кулька відхилилася на кут 100. Визначити заряд кульки.
7. Дві маленькі кульки з однаковими радіусами і масами підвішені на двох нитках так, що їхні поверхні торкаються. Який заряд необхідно надати кулькам, щоб сила натягу ниток дорівнювала 56,4 мН? Довжина кожної нитки 20 см, а маса кожної кульки 5г.
8. Два точкові однойменні заряди 16мкКл перебувають на відстані 10 см один від одного. Визначити напруженість поля в точці, що перебуває на відстані 4 см від першого заряду на прямій, яка сполучає ці заряди.
9. Два точкові однойменні заряди до 12нКл кожен перебувають на відстані 10 см один від одного. Визначити напруженість поля в точці, що перебуває на відстані 8 см від першого заряду та 6 см від другого заряду.
10. Визначити напруженість електричного поля, яке створює в вакуумі нескінченно довга заряджена площина з поверхневою густиною заряду 2 мкКл/м2. Скористатися теоремою Гаусса.
11. Визначити напруженість електричного поля, створеного провідною сферою у воді ( 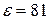 ) поблизу її поверхні. Радіус сфери 5 см, заряд 1нКл. Скористатися теоремою Гаусса.
) поблизу її поверхні. Радіус сфери 5 см, заряд 1нКл. Скористатися теоремою Гаусса.
12. Визначити напруженість електричного поля, створеного провідною сферою радіусом 10 см у вакуумі на відстані 5 см від її поверхні. Поверхнева густина заряду сфери 2нКл/м2. Скористатися теоремою Гаусса. Побудувати графік залежності напруженості електричного поля від відстані від центра сфери.
13. Визначити напруженість електричного поля, створеного зарядженою кулею поблизу її поверхні. Об’ємна густина заряду кулі 4 нКл/м3, радіус – 10 см. Скористатися теоремою Гаусса.
14. Визначити напруженість електричного поля, створеного зарядженою кулею, на відстані 20 см від її поверхні. Об’ємна густина заряду кулі 5нКл/м3, радіус кулі – 10 см. Скористатися теоремою Гаусса. Побудувати графік залежності напруженості електричного поля від відстані від центра кулі.
15. Визначити напруженість електричного поля, створеного в вакуумі двома зарядженими паралельними нескінченно довгими площинами. Поверхнева густина заряду першої площини дорівнює – 4 нКл/м2, другої - +4 нКл/м2. Скористатися теоремою Гаусса.
16. Визначити напруженість електричного поля, створеного тонким зарядженим нескінченно довгим циліндром на відстані 5 см від його осі. Лінійна густина заряду циліндра 5 нКл/м. Скористатися теоремою Гаусса.
17. Точковий заряд 25 нКл міститься в електричному полі, створеному нескінченно довгим циліндром радіусом 1 см, який рівномірно заряджений з поверхневою густиною заряду 0,2 нКл/м2. Визначити силу, яка діє на заряд, якщо він перебуває на відстані 10 см від осі циліндра.
18. Дві концентричні провідні сфери радіусами 6 і 10 см мають відповідно заряди 1 і -0,5 нКл. Визначити напруженість електричного поля в точках, які містяться від центра сфер на відстанях 5 см, 9 см і 15 см. Побудувати графік залежності напруженості електричного поля від відстані 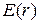 .
.
19. Тонка заряджена нитка, зігнута у вигляді дуги кола, має рівномірно розподілений заряд з лінійною густиною 10нКл/м. Визначити напруженість і потенціал електричного поля, яке вона створює, в точці, що розташована в центрі кривизни дуги. Довжина нитки становить 1/3 довжини кола і дорівнює 15 см.
20. Яка робота відбувається при перенесенні точкового заряду 2 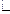 10-8 Кл з нескінченності в точку, що перебуває на відстані 4 см від поверхні кулі радіусом 1 см, зарядженої до потенціалу 6000 В?
10-8 Кл з нескінченності в точку, що перебуває на відстані 4 см від поверхні кулі радіусом 1 см, зарядженої до потенціалу 6000 В?
21. Електричне поле створене зарядженою провідною кулею, потенціал якої дорівнює 300 В. Визначити роботу, яку виконують сили поля з переміщення заряду 0,2 мкКл з точки 1 у точку 2 (рис.6.1).
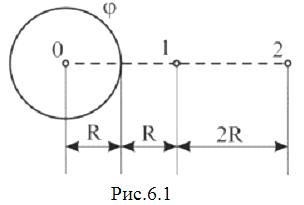
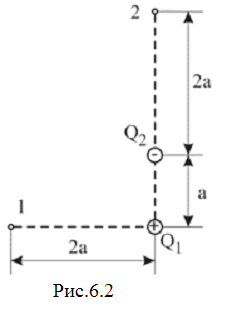
22. Електричне поле створене зарядами +2 мкКл та -2 мкКл, що перебувають на відстані =10 см один від одного. Визначити роботу, яку виконують сили поля, при переміщенні заряду 0,5 мкКл з точки 1 у точку 2 (рис.6.2).
23. Дві паралельні заряджені площини, поверхневі густини заряду яких дорівнюють 2 та -0,8 мкКл/м2, перебувають на відстані 0,6 см одна від одної. Визначити різницю потенціалів між площинами.
24. Тонка квадратна рамка заряджена рівномірно з лінійною густиною заряду 200пКл/м. Визначити потенціал поля в точці перетину діагоналей.
25. Порошина масою 10-9 кг утримується в рівновазі між двома горизонтальними паралельними пластинами, зарядженими до різниці потенціалів 120 В. Відстань між пластинами 8 мм. З яким прискоренням буде рухатися порошина, якщо вона втратить 10 електронів?
26. Порошина масою 200 мкг, що несе на собі заряд 40 нКл, влетіла в електричне поле в напрямі силових ліній. Після проходження різниці потенціалів 200 В порошина мала швидкість 10 м/с. Визначити швидкість порошини до того, як вона влетіла в поле.
27. Електрон, пройшовши в плоскому конденсаторі шлях від однієї пластини до другої, набув швидкість 105 м/с. Відстань між пластинами 6 мм. Визначити напруженість поля та різницю потенціалів між пластинами конденсатора.
28. Електрон, що мав кінетичну енергію 10 еВ, влетів в однорідне електричне поле в напрямі силових ліній поля. Яку швидкість буде мати електрон, пройшовши в цьому полі різницю потенціалів 8 В?
29. Електрон, пройшовши у плоскому конденсаторі шлях від однієї пластини до другої, набув швидкість 105 м/с. Відстань між пластинами дорівнює 8 мм. Знайдіть різницю потенціалів між пластинами та поверхневу густину заряду на пластинах.
30. Порошина масою 5 нг, що несе на собі 10 електронів, пройшла у вакуумі прискорюючу різницю потенціалів 1 МВ. Яку швидкість набула порошина? Яка кінетична енергія порошини?
31. Електрон рухається вздовж силової лінії однорідного електричного поля. У деякій точці поля з потенціалом 100 В електрон мав швидкість 6 Мм/с. Визначити потенціал точки поля, дійшовши до якої електрон втратить половину своєї швидкості.
32. В однорідне електричне поле напруженістю 200 В/м влітає вздовж силової лінії електрон зі швидкістю 2 Мм/с. Визначити відстань, що пройде електрон до точки, в якій його швидкість буде дорівнювати половині від початкової.
33. Три конденсатори ємностями 1, 2 і 3мкФ з’єднані послідовно і підключені до джерела постійного струму з напругою 300 В. Визначити заряд і напругу на обкладках кожного конденсатора.
34. Конденсатор ємністю 10 мкФ заряджений до напруги 10 В. Визначити заряд на обкладках цього конденсатора після того, як паралельно йому було підключено другий, заряджений конденсатор ємністю 20 мкФ.
35. Два конденсатори ємностями 5 і 8 мкФ з’єднані послідовно і приєднані до батареї ЕРС 80 В. Визначити заряди конденсаторів та різницю потенціалів між їхніми обкладками.
36. Плоский конденсатор складається з двох круглих пластин радіусом 10 см кожна. Відстань між пластинами дорівнює 2 мм. Конденсатор приєднаний до джерела напруги 80 В. Визначити заряд конденсатора і напруженість поля конденсатора у двох випадках: а) діелектрик – повітря; б) діелектрик – скло.
37. Простір між пластинами плоского конденсатора заповнений двома шарами діелектрика: шаром скла товщиною 0,2 см та шаром парафіну товщиною 0,3 см. Різниця потенціалів між обкладками дорівнює 300 В. Визначити напруженість поля та падіння потенціалу в кожному із шарів.
38. Плоский конденсатор з площею пластин 200 см2 кожна заряджений до різниці потенціалів 2 кВ. Відстань між пластинами дорівнює 2 см. Діелектриком є скло ( 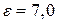 ). Визначити енергію поля конденсатора та густину енергії поля.
). Визначити енергію поля конденсатора та густину енергії поля.
39. Плоский повітряний конденсатор, відстань між обкладками якого 5 мм, заряджений до різниці потенціалів 3000 В. Площа його пластин 15,7 см2. Конденсатор відключається від джерела напруги, а потім його пластини розсовуються на відстань 1 см. Визначити ємність, різницю потенціалів та енергію конденсатора після розсування його пластин.
40. Між пластинами плоского конденсатора, що перебувають на відстані 1 см одна від одної, прикладена різниця потенціалів 100 В. До однієї з пластин прилягає плоско паралельна пластинка кристалічного бромистого талію ( 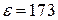 ) товщиною 9,5 мм. Після відключення конденсатора від джерела напруги пластинку кристала виймають. Якою буде після цього різниця потенціалів між пластинами конденсатора?
) товщиною 9,5 мм. Після відключення конденсатора від джерела напруги пластинку кристала виймають. Якою буде після цього різниця потенціалів між пластинами конденсатора?
Зміст
1. Електростатичне поле в вакуумі..........................................................................3
1.1. Електростатика. Електричний заряд та його властивості..........................3
1.2. Закон Кулона..................................................................................................4
1.3. Електричне поле. Напруженість поля..........................................................7
1.4. Робота сил електростатичного поля та його потенціальний характер.....9
1.5. Потенціал електростатичного поля. Еквіпотенціальні поверхні.............11
1.6. Зв’язок між напруженістю та потенціалом електростатичного поля.....13
1.7. Електричний диполь. Поле диполя............................................................14
1.8. Електричний диполь в однорідному та неоднорідному електричних
полях..............................................................................................................16
1.9. Опис властивостей електричного поля......................................................17
1.9.1. Потік вектора напруженості електричного поля 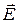 .............................17
.............................17
1.9.2. Теорема Гаусса....................................................................................18
1.9.3. Дивергенція (розходження) вектора 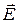 ............................................20
............................................20
1.9.4. Теорема Остроградського – Гаусса...................................................21
1.9.5. Циркуляція вектора 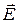 ........................................................................21
........................................................................21
1.9.6. Ротор вектора 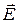 ..................................................................................22
..................................................................................22
1.9.7. Теорема Стокса...................................................................................23
1.9.8. Розрахунок полів із застосуванням теореми Гаусса........................24
2. Електричне поле в діелектриках........................................................................26
2.1. Діелектрики. Полярні та неполярні молекули. Поляризація діелект-
риків................................................................................................................26
2.2. Опис електричного поля в діелектриках....................................................29
2.3. Приклади обчислення поля в діелектриках...............................................31
2.4. Умови на межі поділу двох діелектриків...................................................33
2.5. Сегнетоелектрики.........................................................................................35
2.6. П’єзоелектричний ефект. Електрострикція...............................................36
3. Провідники в електричному полі......................................................................37
3.1. Розподіл електричних зарядів на провіднику...........................................37
3.2. Провідник у зовнішньому електричному полі..........................................38
3.3. Електрична ємність. Конденсатори............................................................39
4. Енергія електричного поля.................................................................................42
4.1. Енергія системи електричних зарядів........................................................42
4.2. Енергія зарядженого провідника................................................................43
4.3. Енергія зарядженого конденсатора............................................................43
4.4. Енергія електричного поля..........................................................................44
5. Приклади розв’язування задач...........................................................................44
6. Задачі для самостійного розв’язування.............................................................56
Література
1. Кучерук І.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики.Т.2.-К.;Тех-
ніка, 2001.
2. Угаров В.А. Специальная теория относительности. М.; Наука, 1969.
3. Яворский Б.М., Детлаф А.А., Милковская Л.Б. Курс физики. Т.2. – М.; Выс-
шая школа, 1972.
4. Савельев И.В. Курс общей физики. Т.1. – М.; Наука, 1977.
5. Біленко І.І. Фізичний словник. – К.; Вища школа, 1979.
6. Иродов И.Е. Задачи по физике. – М.; Наука, 1988.
7. Чертов Н.О., Воробьёв А.П. Сборник задач по физике. – М.; Высшая школа,
1980.
8. Воловик П.М. Фізика для університетів. – К.; Ірпінь; Перун, 2005.








