4 . Енергія електричного поля

Дата: 2025-06-02; Просмотры: 8

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

4.1. Енергія системи електричних зарядів

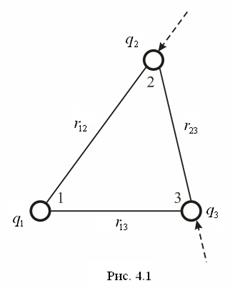Закріпимо точковий заряд q ₁ в точці 1 (рис. 4.1). Обчислимо роботу А₁ при перенесенні точкового заряду q ₂ із нескінченності в точку 2. Згідно з співвідношенням (1.15)

.

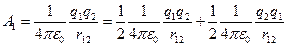Робота А₂ при переміщенні точкового заряду q ₃ із нескінченності в точку 3

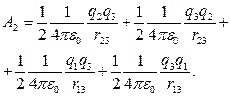
Сумарна робота кількісно дорівнює потенціальній енергії взаємодії цих зарядів:

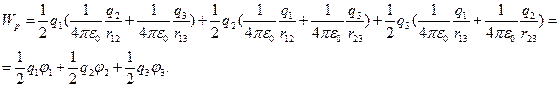
Тут 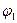- потенціал поля створений зарядами q ₂ і q ₃, в точці, де знаходиться

заряд q ₁ і т. д.

Потенціальна енергія системи n точкових зарядів:

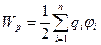, (3.6)

де 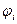- потенціал поля, створений всіма n -1 зарядами в тій точці, де знаходиться заряд q_i.

4.2. Енергія зарядженого провідника

Заряд q, що знаходиться на деякому провіднику, можна розглядати як систему точкових зарядів D q. Поверхня провідника є еквіпотенціальною. Тому потенціали тих точок, в яких знаходяться точкові заряди D q, однакові і дорівнюють потенціалу 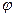провідника. Скориставшись формулою (3.6), отримаємо для енергії зарядженого провідника вираз

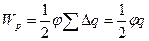. (3.7)

На підставі формул (3.1) і (3.7) отримаємо:

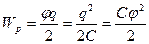, (3.7)

4.3. Енергія зарядженого конденсатора

Оскільки заряди обкладок конденсатора мають різні знаки, то для конденсатора, згідно (3.6) отримаємо:

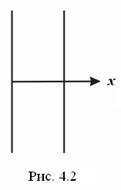
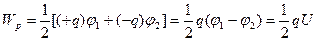. (3.9)

Враховуючи (3.3) та (3.9) знаходимо:

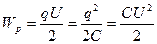. (3.10)

Знайдемо силу, з якою пластини плоского конденсатора притягують одна іншу. Зв’яжемо початок осі 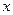з лівою пластинкою (рис. 3.5).

Тоді координата 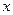другої пластини буде визначати зазор 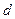між обкладками. Згідно з (3.5) та (3.10) знаходимо, що 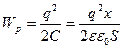. Сила, що діє на праву пластину в напрямі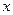

.

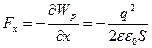За величиною сила, з якою пластини притягують одна другу дорівнює

.

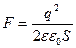4.4. Енергія електричного поля

Розглянемо енергію зарядженого плоского конденсатора, скориставшись співвідношеннями: 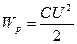; ; 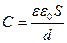; 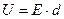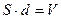- об’єм конденсатора. Тоді

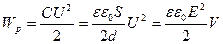. (3.11)

Формула (3.11) отримана на прикладі поля, створеного зарядами обкладок конденсатора.

Якщо поле неоднорідне, то його енергія, зосереджена в певному об’ємі 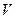, може бути визначена за формулою:

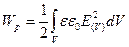. (3.12)

Це рівняння виражає електричну енергію у вигляді нескінченної суми досить малих доданків, кожний з яких дорівнює 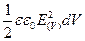і належить певному елементові об’єму 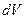. Тому в рівняння (3.11) та (3.12) можна вкласти такий фізичний зміст: носієм електричної енергії є електричне поле, енергія якого локалізована у просторі так, що у випадку 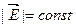в кожній одиниці об’єму зосереджена енергія

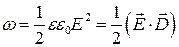, (3.13)

де 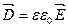- вектор електричного зміщення (індукції).

Величину 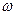називають об’ємною густиною енергії електростатичного поля. Це свідчить про те, що електрична енергія розподілена в просторі з певною об’ємною густиною, що цілком відповідає концепції близькодії.

5. Приклади розв’язування задач.

5.1. Дві невеликі однакові заряджені кульки, кожна маси 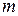, підвішені в одній точці на умовно нерозтяжних нитках довжиною 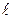. Відстань між кульками 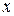<< 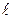. Знайти швидкість стікання зарядів 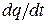з кожної кульки, якщо швидкість їх зближення змінюється за законом 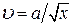, де 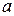-стала.

Розв’язування.

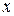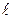<< Умовно зафіксуємо миттєвий стан системи як рівноважний.

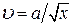Оскільки система симетрична відносно вертикалі, що проходить

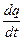-? через точку підвісу, то доцільно розглянути сили, які діють на одну

кульку (рис.5.1). У стані рівноваги векторна сума всіх цих сил дорівнює нулеві:

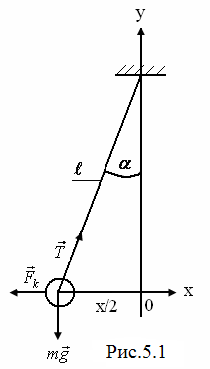
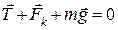. (а)

Тут 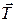- реакція нитки, 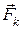- кулонівська сила взаємодії між кульками, 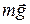- сила тяжіння. Запишемо рівняння (а) у проекціях на координатні осі x та y:

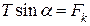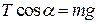; . (б)

Сумісне рішення системи рівнянь (б) дає рівняння

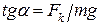. (в)

Оскільки 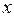<< 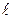, то можна прийняти, що 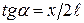. Враховуючи закон Кулона, на підставі 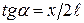(в) отримуємо:

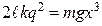. (г)

Продиференціювавши ліву та праву частини рівняння (г), маємо:

.

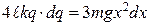Прийнявши, що за малий проміжок часу 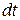зближення кульок 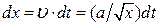і враховуючи, що згідно з рівнянням (г)

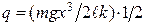і що 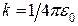, знаходимо кінцеве рівняння у загальному вигляді:

.

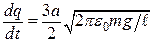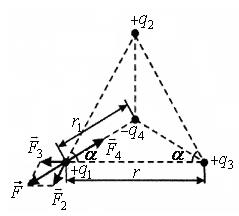
5.2. Три точкові однакові позитивні заряди 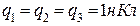розміщені у вершинах рівностороннього трикутника (рис.5.2). Який негативний точковий заряд 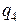потрібно помістити в центр трикутника, щоб сила притягання з його боку зрівноважила сили взаємного відштовхування зарядів, які знаходяться у вершинах?

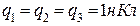Розв’язування.

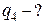Заряд 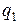перебуватиме в рівновазі, якщо векторна сума діючих на нього сил дорівнюватиме нулеві:

,

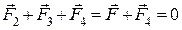де 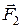, 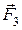і 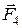- сили, з якими діють на заряд 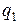відповідно заряди 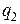, 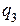і 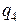; 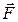- рівнодійна сил 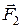і .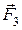

Оскільки сили 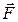і 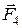напрямлені по одній прямій, то з (а) випливає, що 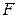- 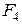=0, або 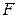= 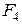. Виразивши в останньому рівнянні

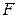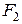через і 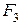і врахувавши, що = ,

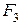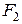Рис.5.2 дістанемо:

.

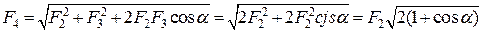Згідно із законом Кулона і з урахуванням, що 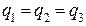, знайдемо

,

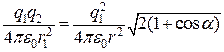звідки

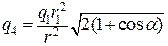. (б)

З геометричних побудов у рівносторонньому трикутнику

.
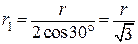