Електричне поле в плоскій пластині
Нехай поле, створюване різнойменно зарядженими нескінченими площинами в вакуумі, характеризується напруженістю 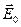 і зміщенням
і зміщенням 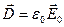 (для вакууму
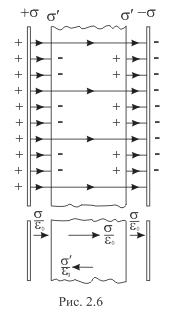
(для вакууму 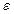 =1). Вмістимо в це поле пластину із однорідного діелектрика так, як показано на рис 2.6. Під дією поля діелектрик поляризується і на його поверхнях виникають зв’язані заряди з поверхневою густиною
=1). Вмістимо в це поле пластину із однорідного діелектрика так, як показано на рис 2.6. Під дією поля діелектрик поляризується і на його поверхнях виникають зв’язані заряди з поверхневою густиною 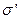 . Ці заряди створюють внутрішнє поле напруженістю
. Ці заряди створюють внутрішнє поле напруженістю 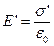 .
.
За межами діелектрика це поле відсутнє. Напруженість сумарного поля в межах діелектрика
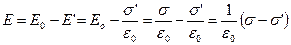 , (2.16)
, (2.16)
за межами діелектрика 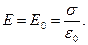
Поляризація діелектрика зумовлена цим сумарним полем напруженістю E. Це поле перпендикулярне до поверхонь пластини. Тому 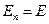 і згідно з (2.6) та (2.9) на підставі співвідношення (2.16) отримуємо:
і згідно з (2.6) та (2.9) на підставі співвідношення (2.16) отримуємо:
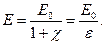 (2.17)
(2.17)
Таким чином, в розглянутому випадку діелектрична проникність 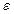 показує, у скільки разів діелектрик послаблює поле.
показує, у скільки разів діелектрик послаблює поле.
Домноживши (2.17) на 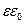 , отримаємо електричне зміщення в пластині
, отримаємо електричне зміщення в пластині
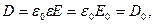 (2.18)
(2.18)
де 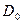 - електричне зміщення в вакуумі. Замінивши в (2.18)
- електричне зміщення в вакуумі. Замінивши в (2.18) 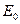 через
через 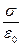 , знайдемо, що
, знайдемо, що
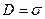 , (2.19)
, (2.19)
де 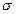 - поверхнева густина вільних (сторонніх ) зарядів.
- поверхнева густина вільних (сторонніх ) зарядів.
Використавши (2.16), (2.17) та (2.19), знайдемо поверхневу густину зв’язаних зарядів 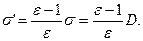 (2.20)
(2.20)
Поле всередині кульового шару
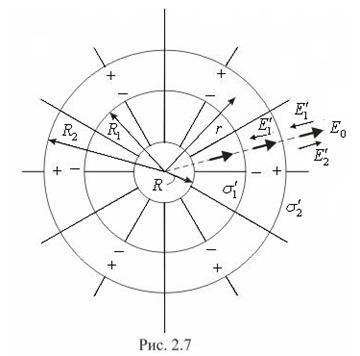 Охопимо заряджену сферу радіуса R концентричним кульовим шаром із однорідного ізотропного діелектрика (рис. 2.7). На внутрішній поверхні шару виникає зв’язаний заряд
Охопимо заряджену сферу радіуса R концентричним кульовим шаром із однорідного ізотропного діелектрика (рис. 2.7). На внутрішній поверхні шару виникає зв’язаний заряд 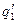 , розподілений з густиною
, розподілений з густиною 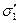 (
( 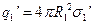 ), на зовнішній - заряд
), на зовнішній - заряд 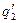 , розподілений з густиною
, розподілений з густиною 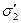 (
( 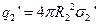 ). Знак заряду
). Знак заряду 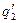 співпадає з знаком заряду
співпадає з знаком заряду 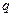 сфери, знак
сфери, знак 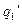 протилежний йому. Заряди
протилежний йому. Заряди 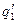 і
і 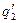 створюють на відстані
створюють на відстані 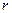 , більшій відстаней
, більшій відстаней 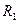 та
та 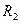 , поле, таке саме, як поле точкового заряду такої ж величини. Під поверхнями, на яких вони розподілені, заряди
, поле, таке саме, як поле точкового заряду такої ж величини. Під поверхнями, на яких вони розподілені, заряди 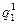 і
і 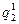 поля не створюють. Отже, напруженість
поля не створюють. Отже, напруженість 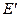 поля в об’ємі діелектрика дорівнює
поля в об’ємі діелектрика дорівнює 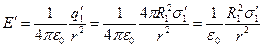
і протилежна за напрямом напруженості 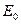 . Напруженість сумарного поля в об’ємі діелектрика
. Напруженість сумарного поля в об’ємі діелектрика
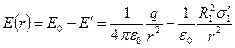 (2.21)
(2.21)
зменшується за законом 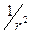 . Тому можна прийняти, що
. Тому можна прийняти, що 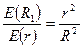 , тобто
, тобто 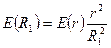 , де
, де 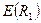 – напруженість поля в діелектрику біля внутрішньої поверхні шару. Саме ця напруженість визначає величину
– напруженість поля в діелектрику біля внутрішньої поверхні шару. Саме ця напруженість визначає величину 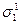 :
:
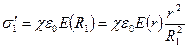 (2.22)
(2.22)
(в кожній точці поверхні 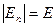 ).
).
Підставивши вираз (2.22) в форму (2.21), отримаємо:
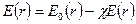 ,
,
звідки знаходимо, що в середині діелектрика 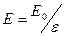 , отже
, отже 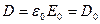 , що співпадає з (2.18).
, що співпадає з (2.18).
Отже, взагалі напруженість поля в діелектрику в ε разів менша напруженості поля в вакуумі.
2.4. Умови на межі поділу двох діелектриків
Внесемо в однорідне поле напруженістю 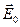 дві плоско паралельні однорідні пластини з різних діелектриктриків (рис.2.8).
дві плоско паралельні однорідні пластини з різних діелектриктриків (рис.2.8).
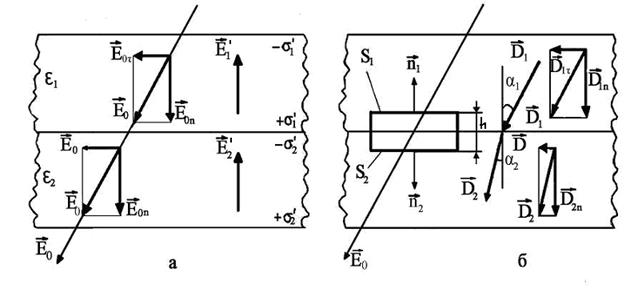 Рис.2.8
Рис.2.8
Під дією зовнішнього поля діелектрики поляризуються і в них виникнуть внутрішні поля напруженостей 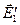 і
і 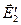 . Оскільки діелектрики різні, то
. Оскільки діелектрики різні, то 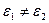 і
і 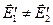 . У діелектриках будуть сумарні поля, напруженості яких
. У діелектриках будуть сумарні поля, напруженості яких
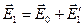 ;
; 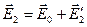 . (2.23)
. (2.23)
Відповідно напруженостям для електричних зміщень можна записати:
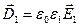 ;
; 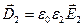 . (2.24)
. (2.24)
Вектори  і
і 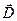 , подібно вектору
, подібно вектору 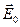 (рис.2.8,а), можна подати в вигляді нормальних та дотичних (тангенціальних) до межі поділу складових в кожному з діелектриків.
(рис.2.8,а), можна подати в вигляді нормальних та дотичних (тангенціальних) до межі поділу складових в кожному з діелектриків.
Оскільки вектори 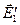 і
і 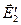 перпендикулярні до межі поділу двох середовищ, а дотичні складові в кожному з діелектриків
перпендикулярні до межі поділу двох середовищ, а дотичні складові в кожному з діелектриків 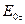 однакові, то очевидно, що
однакові, то очевидно, що
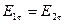 і
і 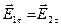 . (2.25)
. (2.25)
На підставі співвідношень (2.24) для дотичних складових та (2.25) отримаємо:
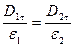 , або
, або 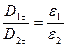 . (2.26)
. (2.26)
Знайдемо співвідношення між нормальними складовими векторів  та
та 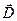 в кожному з діелектриків. Для цього розглянемо уявний циліндр дуже малої висоти
в кожному з діелектриків. Для цього розглянемо уявний циліндр дуже малої висоти 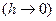 , основи якого S 1 і S 2 розташовані по різні сторони поверхні поділу (рис.2.8,б). Оскільки вільних зарядів в об’ємі цього циліндра немає, то потік вектора
, основи якого S 1 і S 2 розташовані по різні сторони поверхні поділу (рис.2.8,б). Оскільки вільних зарядів в об’ємі цього циліндра немає, то потік вектора 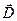 через поверхню циліндра дорівнює нулеві:
через поверхню циліндра дорівнює нулеві: 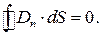 За умови, що
За умови, що 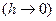 потік вектора
потік вектора 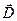 через бокову поверхню буде нескінченно малий, і його величиною можна знехтувати. Тоді теорему Гаусса можна записати у вигляді:
через бокову поверхню буде нескінченно малий, і його величиною можна знехтувати. Тоді теорему Гаусса можна записати у вигляді: 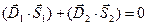 . Зважаючи на взаємно протилежні напрями нормалей
. Зважаючи на взаємно протилежні напрями нормалей 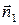 та
та 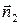 , проектуючи вектори
, проектуючи вектори 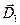 і
і 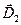 на одну нормаль до межі поділу діелектриків, знаходимо, що
на одну нормаль до межі поділу діелектриків, знаходимо, що
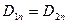 . (2.27)
. (2.27)
Приймаючи, що співвідношення (2.24) є вірним і для нормальних складових, враховуючи (2.27), отримуємо, що
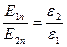 . (2.28)
. (2.28)
Аналіз співвідношень (2.25) – (2.28) призводить до висновку, що дотичні складові вектора  та нормальні складові вектора
та нормальні складові вектора 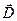 при переході межі поділу двох діелектриків змінюються безперервно. Дотичні складові вектора
при переході межі поділу двох діелектриків змінюються безперервно. Дотичні складові вектора 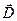 та нормальні складові вектора
та нормальні складові вектора  , переходячи межу поділу, розриваються.
, переходячи межу поділу, розриваються.
Оскільки 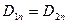 , а
, а 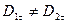 , то очевидно, що лінії вектора
, то очевидно, що лінії вектора 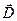 на межі поділу заломлюються (рис.2.8,б). Знайдемо співвідношення між кутами a 1 і a2. Із рис.2.8, б та формул (2.26) і (2.27) знаходимо:
на межі поділу заломлюються (рис.2.8,б). Знайдемо співвідношення між кутами a 1 і a2. Із рис.2.8, б та формул (2.26) і (2.27) знаходимо:
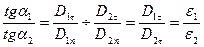 . (2.29)
. (2.29)
Оскільки діелектрики різні 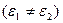 то і
то і 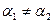 .
.
2.5. Сегнетоелектрики
Існує група полярних кристалічних діелектриків, які в певному інтервалі температур спонтанно поляризовані (див.§2.1). Це явище вперше було виявлено для сегнетової солі, в зв’язку з чим всі подібні речовини отримали назву сегнетоелектриків.
Сегнетоелектрики відрізняються від інших діелектриків рядом характерних особливостей:
1.Якщо діелектрична проникність e у звичайних діелектриків складає кілька одиниць (іноді кілька десятків), у сегнетоелектриків вона може досягати кількох тисяч.
2.Залежність Р від E не є лінійною (див. крива 1 на рис.2.9). Отже, згідно з формулами (2.6) і (2.14) діелектрична проникність складним чином залежить від напруженості поля E.
3. Зі зміною напруженості E значення поляризованості P і електричного зміщення D відстають від напруженості, внаслідок чого P і D визначаються не тільки величиною E в даний момент, а і попереднім значенням E, тобто залежать від передісторії діелектрика. Це явище називають гістерезисом.
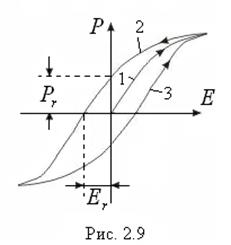 За циклічних змін поля залежність P від E описується замкненою кривою (рис.2.9), яку називають петлею гістерезису. При початковому вмиканні поля поляризованість P зростає зі збільшенням E відповідно кривій 1. Зі зменшенням напруженості поля зміна поляризації відбувається за кривою 2. При досягненні E =0 поляризація має деяке залишкове значення Pr. Залишкова поляризація зникає тільки при накладанні певного електричного поля Er протилежного напряму. Це значення напруженості називають коерцитивною силою діелектрика. За подальшої зміни E величина P змінюється по кривій 3 петлі гістерезису і т.д. Така поведінка сегнетоелектриків зумовлена їх доменною структурою (див.§2.1.).
За циклічних змін поля залежність P від E описується замкненою кривою (рис.2.9), яку називають петлею гістерезису. При початковому вмиканні поля поляризованість P зростає зі збільшенням E відповідно кривій 1. Зі зменшенням напруженості поля зміна поляризації відбувається за кривою 2. При досягненні E =0 поляризація має деяке залишкове значення Pr. Залишкова поляризація зникає тільки при накладанні певного електричного поля Er протилежного напряму. Це значення напруженості називають коерцитивною силою діелектрика. За подальшої зміни E величина P змінюється по кривій 3 петлі гістерезису і т.д. Така поведінка сегнетоелектриків зумовлена їх доменною структурою (див.§2.1.).
Поведінка поляризованості сегнетоелектриків аналогічна поведінці намагніченості феромагнетиків. З цієї причини сегнетоелектрики іноді називають фероелектриками.








