Величину , що визначається рівнянням (2.5), називають вектором поляризації або поляризуємістю діелектрика. Розмірність . В системі СІ одиницею виміру P є Кл/м2.
Для ізотропних діелектриків всіх типів виконується співвідношення:
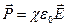, (2.6)
де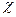 
- діелектрична сприйнятливість діелектрика.
Якщо молекули неполярні, то, згідно з (2.4),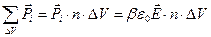 
і 
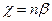, де n – число молекул в одиниці об’єму.
Взагалі відрізняють такі види поляризації:
1) Пружна поляризація електронного чи іонного зміщення. В зовнішньому полі неполярні молекули стають полярними і їх електричні моменти орієнтуються полем. Іонні кристали можна розглядати як речовини, що складаються з двох підрешіток (позитивної і негативної), вставлених одна в іншу. Під дією поля ці підрешітки зміщуються одна відносно іншої, діелектрик поляризується. Неполярні молекули і іонні кристали можна в електричному полі розглядати як пружні диполі.
2) Дипольна поляризація – орієнтація дипольних моментів полярних молекул силами зовнішнього поля. Полярні молекули можна розглядати в зовнішньому полі як жорсткі диполі.
3) 
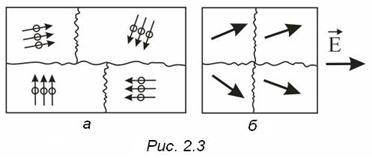Спонтанна (довільна) поляризація, що спостерігається для речовин з доменною структурою (рис. 2.3). Домени – це мікрообласті матеріалу, в яких електричні моменти самочинно, внаслідок обмінної взаємодії електронами між молекулами, орієнтуються майже паралельно один одному. За відсутності поля моменти доменів орієнтуються хаотично (рис. 2.3,а), а за наявності електричного поля їх орієнтація упорядковується (рис. 2.3,б). Спонтанна поляризація притаманна кристалічним речовинам.
4) Об’ємно – зарядна поляризація – зміщення слабко зв’язаних зарядів під дією сил поля.
2.2. Опис електричного поля в діелектриках
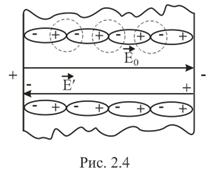В зовнішньому електричному полі діелектрик поляризується. Якщо діелектрик однорідний, то внаслідок поляризації внутрішні зв’язані заряди двох сусідніх молекул взаємно компенсуються (рис. 2.4). Нескомпенсованими залишаються заряди на протилежних поверхнях. Ці заряди (позначимо їх q ’) утворюють внутрішнє поле напруженістю 
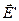, орієнтованою антипаралельно напруженості 
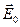зовнішнього поля. Згідно з принципом суперпозиції полів напруженість сумарного поля в діелектрику буде:
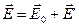. (2.7).
Саме ця напруженість розглядається в формулах (2.4) та (2.6). Досвід свідчить, що всі основні положення теорії електричного поля в вакуумі можна використовувати при дослідженні поля в речовині, враховуючи електричні властивості самої речовини.
Для сумарного поля 
в діелектриках теорему Гаусса можна записати в такому вигляді:
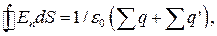(2.8)
де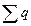 
- сума вільних зарядів, що створюють зовнішнє поле напруженістю , 
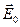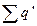- сума зв’язаних зарядів в об’ємі діелектрика. 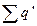не піддається точному розрахунку. Однак її можна виразити через макроскопічну характеристику, яку можна виміряти експериментально.
В однорідному поляризованому діелектричному тілі умовно виділимо деякий об’єм (рис.2.5).
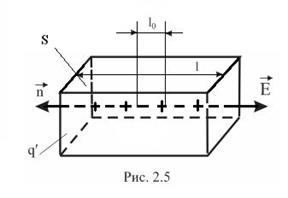Кожна пара зарядів 
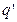є диполь довжиною l 0. Електричний момент кожного диполя 
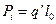. Електричний момент всього ланцюжка дорівнює 
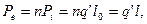де n – кількість молекул у ланцюжку. Для всіх N ланцюжків, що перетинають площину S, електричний момент ( момент всього розглянутого тут об’єму діелектрика) дорівнює 
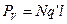. Весь ланцюжок можна розглядати як один диполь з зарядом 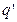і довжиною l, оскільки внутрішні заряди можна розглядати як взаємно скомпенсовані. Тоді 
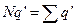, і модуль вектора поляризації
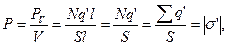(2.9)
де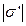 
- поверхнева густина зв’язаних зарядів.
Враховуючи напрям вектора поляризації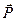 
в електричному полі, на підставі формули (2.9) та рис . 2.5 знаходимо, що 
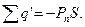Тоді співвідношення (2.8) набирає вигляду:
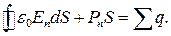(2.10)
Оскільки вектори 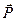і за напрямом співпадають, то співвідношення (2.10) можна записати у такому вигляді:
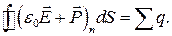(2.11)
Величину
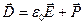(2.12)
називають вектором електричного зміщенні або індукцією електричного поля. Одиницею виміру електричного зміщення в СІ є В·Ф/м2=Кл/м2.
На підставі (2.6) та (2.12) знаходимо, що для однорідного діелектрика
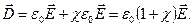(2.13)
Безрозмірну величину
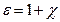(2.14)
називають відносною діелектричною проникністю середовища.
Враховуючи (2.13) та (2.14), знаходимо, що для однорідного діелектрика
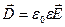. (2.15)
Для вектора електричного зміщенні формула Гаусса набирає вигляду:
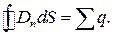
За нерівномірної об’ємної густини заряду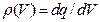 
отримуємо:
,
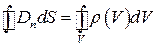за рівномірної
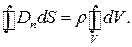
Враховуючи теорему Остроградського–Гаусса (1.50), отримуємо:
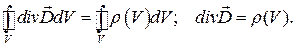
Поле вектора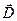 
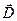можна описати з допомогою ліній електричного зміщення, які проводяться за таким самим принципом, як і лінії напруженості . Джерелом ліній можуть бути тільки вільні заряди. Через точки, в яких знаходяться зв’язані заряди, лінії зміщення проходять, не розриваючись.
2.3. Приклади обчислення поля в діелектриках
Щоб вияснити фізичний зміст величин 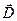і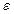 
, розглянемо деякі приклади полів в діелектриках.