У формулах (1.2) – (1.5) − одиничний вектор з напрямком від заряду q 1 до заряду q 2 вздовж прямої, що з’єднує центри зарядів: , а в загальному випадку .

Дата: 2025-06-02; Просмотры: 9

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Враховуючи значення 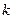і 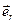закон Кулона у векторній формі в системі CI для системи двох зарядів можна записати в вигляді:

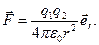(1.6)

Таку форму запису закону Кулона називають раціоналізованою. Вона зручна тим, що при її використанні в багатьох формулах електродинаміки зникають співмножники 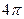та електродинамічна стала С, що кількісно дорівнює швидкості світла в вакуумі. В системі CI коефіцієнт пропорційності

.

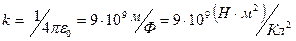Згідно з законом Кулона два точкові заряди взаємодіють між собою в вакуумі з силою F, величина якої прямо пропорційна добутку зарядів q ₁ та q ₂ і обернено пропорційна квадрату відстані r між ними.

Розрахунки показують, що закон Кулона у формі (1.1), а також (1.6) вірно описує взаємодію заряджених тіл кулястої форми, якщо заряди q ₁ і q ₂ розподілені рівномірно по всьому об’ємі або по всій поверхні цих куль. При цьому радіуси куль можуть бути сумірними з відстанню r між їхніми центрами.

Досвід свідчить про те, що сила взаємодії двох точкових зарядів не залежить від наявності інших зарядів. Якщо на обраний точковий заряд q ₀ діють n інших точкових зарядів q _і, то сила, з якою всі q _і заряди діють на заряд q ₀, дорівнює векторній сумі сил окремих зарядів:

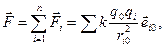(1.7)

де 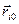– радіус-вектор, проведений від заряду q _і до заряду q ₀.

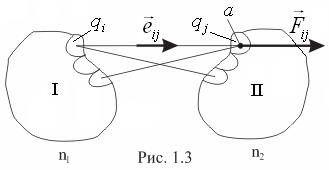Це твердження називають принципом суперпозиції сил, а сам принцип дозволяє використати закон Кулона для неточкових заряджених тіл. Для цього подумки треба поділити ці тіла на елементи (рис.1.3), які можна вважати точковими зарядами.

Сила взаємодії між зарядженими тілами буде виражатись векторною сумою сил, прикладених до всіх зарядів другого тіла з боку кожного точкового заряду першого тіла:

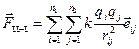. (1.8)

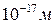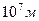Важливим є питання про межі застосування закону Кулона. Досвіди свідчать про те, що закон Кулона справджується в межах від до [1].

1.3 . Електричне поле. Напруженість поля

Згідно з концепцією близькодії (див.[1],[3]) будь-який електричний заряд змінює властивості навколишнього середовища – створює електричне поле, котре діє на внесений в нього інший заряд. Сила цієї дії визначається законом Кулона.

Поняття поля не є формально введеним. Поле, як і речовина, є формою існування матерії і являє собою об’єктивну реальність, яка існує незалежно від нашої свідомості.

Поля, незмінні з часом, створювані нерухомими зарядами, називають електростатичними.

Властивості електричного поля вивчають за допомогою певного точкового заряду, значення якого має бути досить малим, щоб запобігти спотворення початкового характеру поля.

Нехай нерухомий точковий заряд q створює електричне поле. Внесемо пробний заряд q ₀ в точку, положення якої відносно заряду q визначається радіусом – вектором 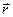(рис.1.4). Згідно з законом Кулона (1.6) на пробний заряд у вибраній точці діє сила

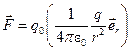(1.9)

Ця сила залежить не лише від заряду q і радіуса-вектора 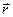, а і від заряду q ₀. Якщо в одну і ту ж саму точку поля, що створюється зарядом q, вносити різні пробні заряди 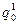, 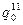і т.п., то на них будуть діяти різні сили 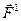, 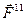і т.п. Однак відношення 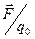для всіх пробних зарядів буде однаковим і залежатиме лише від величин 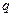і 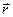, що визначають поле певного заряду в вибраній точці. Тому цю величину і приймають за силову характеристику електричного поля. Її називають вектором напруженості (напруженістю) електричного поля:

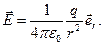(1.10)

Згідно з рівняннями (1.9) та (1.10) напруженість електричного поля кількісно дорівнює силі, з якою поле діє на одиничний заряд, що знаходиться в вибраній точці поля. Очевидно, що напруженість поля є величиною локальною: кожна точка простору навколо зарядженого тіла характеризується цілком конкретним значенням напруженості.

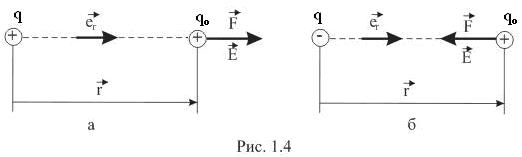
Спрямований вектор уздовж радіальної прямої, що проходить через заряд і дану точку поля від заряду, якщо він позитивний (рис.1.4, а), і до заряду, якщо він негативний (рис.1.4, б).

На підставі рівняння (1.10) знаходимо, що у всіх рівновіддалених від заряду точках напруженість поля за величиною однакова. Отже, поле точкового заряду є центральним і сферично – симетричним.

Згідно з принципом суперпозиції сил (1.7) та співвідношення (1.10) знаходимо, що напруженість поля, яке створюється системою n точкових зарядів, дорівнює векторній сумі напруженостей полів окремих зарядів:

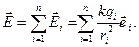(1.11)

Це твердження називають принципом суперпозиції полів. Він дає можливість визначити напруженість поля, що створюється неточковим зарядженим тілом в довільно вибраній точці. Так, якщо заряджене тіло I (рис 1.3) створює поле, то його напруженість в точці а дорівнює:

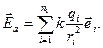
При неперервному об’ємному розподілі зарядів напруженість поля визначається за формулою:

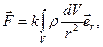
де 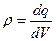– об’ємна густина заряду.

Якщо відомий точковий заряд 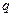внести в певну точку поля з напруженістю , то згідно з (1.10) поле діятиме на заряд з силою

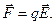(1.12)

У (1.12) необхідно враховувати знак заряду. Якщо заряд q позитивний, то вектори 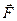і співпадають за напрямком; якщо q негативний, то вектори антипаралельні.

В СІ за формулою (1.10) напруженість електричного поля вимірюють у ньютонах на кулон (Н/Кл) або вольтах на метр (В/м). За одиницю напруженості електричного поля в СІ взято напруженість у такій точці поля, в якій на заряд в 1Кл діє сила в 1Н.

Електричне поле можна описати, вказавши для кожної точки величину і напрямок вектора . Сукупність таких векторів утворює поле вектора напруженості електричного поля. Англійський фізик М.Фарадей запропонував представляти електричне поле за допомогою ліній напруженості. Їх назвали лініями Фарадея. Вони проводяться таким чином, що напрям дотичної до лінії у кожній точці збігається з напрямом напруженості у цій точці, а густина ліній (їх кількість на одиничну площу перпендикулярного перетину) дорівнювала б величині напруженості поля. Оскільки в кожній точці поля вектор є лише певним, то ясно, що силові лінії вектора не перетинаються (рис. 1.5).

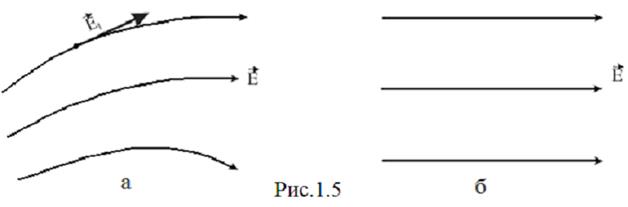
а) поле неоднорідне; б) поле однорідне.

Лінії вектора поля точкового заряду утворюють сукупність радіальних прямих, напрямлених від заряду, якщо він позитивний, і до заряду, якщо він негативний (рис.1.6).

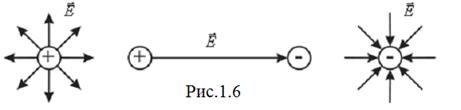
Лінії одним кінцем опираються на заряд, іншим уходять в нескінченність. За позитивний напрямок вектора приймається напрямок від позитивного заряду до негативного.

1.4. Робота сил електростатичного поля та його потенціальний характер

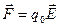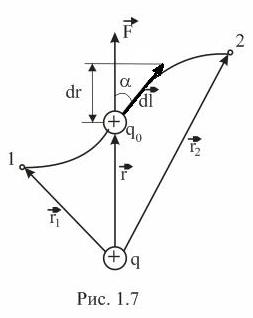
Припустимо, що нерухомий точковий заряд q створює електростатичне поле з напруженістю . На заряд q₀, вміщений у довільну точку цього поля діє сила . Якщо заряд q₀ не закріплений, то сила 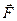примусить його переміщуватись і буде виконувати роботу. Нехай на заряд q₀ окрім сили поля діють реакції зв’язку таким чином, що він може рухатись по довільній траєкторії (рис. 1.7).

Визначимо роботу А₁₂ при переміщені заряду q ₀ із точки 1 в точку 2. Робота d А на елементарній ділянці траєкторії dl дорівнює

.

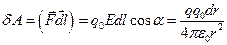Повна робота на шляху 1-2

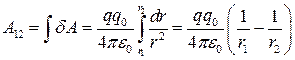. (1.13)

Якщо заряди q і q ₀ однойменні, то робота сил відштовхування А₁₂>0 при віддалені зарядів один від одного і A ₁₂ <0 при їх зближенні. Якщо заряди q і q₀ різнойменні, то все навпаки.

Із формули (1.13) видно, що робота сил електростатичного поля не залежить від форми шляху переміщення заряду між точками 1 і 2, а визначається лише розміщенням початкової 1-(r ₁) і кінцевої 2-(r ₂) точок. Силові поля, які задовольняють таку умову, називають потенціальними або консервативними. Отже, електростатичне поле точкового заряду є потенціальним. Згідно з принципом суперпозиції електричних полів цей висновок можна поширити на випадок електричних полів будь-якої системи нерухомих зарядів.

Робота сил консервативного поля може бути виражена через зміну потенціальної енергії:

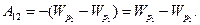(1.14).

Співставляючи формули (1.13) та (1.14), знаходимо, що потенціальна енергія заряду q ₀ в точках 1 і 2 поля, що утворюється зарядом q, може бути представлена у вигляді рівнянь:

; .

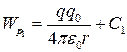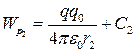Потенціальна енергія визначається з точністю до деякої сталої. Її вибирають таким чином, щоб при віддалені на нескінченність (r ® ¥) потенціальна енергія дорівнювала нулеві. Тоді потенціальна енергія взаємодії двох точкових зарядів q ₁ та q ₂ дорівнює:

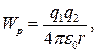(1.15)

де r – відстань між зарядами.

На підставі формули (1.13) знаходимо, що за r ₂ ® ¥

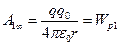. (1.16)

Отже, потенціальна енергія одного заряду в обраній точці поля іншого заряду чисельно дорівнює роботі сил поля при переміщенні першого заряду із цієї точки поля в нескінченність, або роботі проти сил поля при переміщенні точкового заряду із нескінченності в обрану точку поля.

З формули (1.13) випливає, що при переміщенні точкового заряду в електростатичному полі по довільному замкненому контуру (r ₁ = r ₂) робота дорівнює нулеві:

.

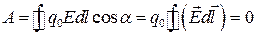Оскільки q ₀ ¹ 0, то

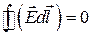. (1.17)

Лінійний інтеграл 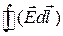, обчислений за довільним замкненим контуром L, називають циркуляцією вектора . Рівняння (1.17) є одним із фундаментальних рівнянь електростатики, яке відображає той факт, що силові лінії електростатичного поля є незамкненими.

1.5. Потенціал електростатичного поля. Еквіпотенціальні поверхні

З формули (1.16) видно, що різні за величиною пробні заряди 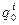в одній тій самій точці поля матимуть різні значення потенціальної енергії 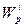. Однак відношення 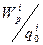буде однаковим для всіх пробних зарядів. Це відношення, що визначається формулою:

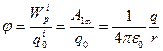(1.18)

називають потенціалом поля в вибраній точці і використовують як енергетичну характеристику поля.

Отже, потенціал електростатичного поля – це фізична величина, що чисельно дорівнює роботі, яку виконують сили поля при переміщенні пробного одиничного заряду із заданої точки в нескінченність (або в точку, для якої потенціал умовно можна вважати таким, що дорівнює нулеві).

З рівності 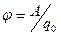визначаємо одиницю потенціалу. В СІ .

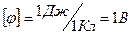І потенціальна енергія і потенціал – величини скалярні. Потенціали точок поля позитивного заряду вважають додатними, а негативного – від’ємними.

З рівності (1.18) випливає, що потенціальна енергія заряду q в точці поля з потенціалом 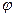дорівнює:

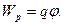(1.19)

Тоді, згідно з рівнянням (1.14), роботу сил поля над зарядом можна визначити через різницю потенціалів:

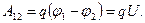(1.20)

Робота 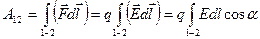. Враховуючи (1.16) та (1.20), знаходимо різницю потенціалів поля між двома точками:

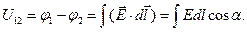(1.21)

Якщо поле створюється системою 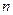точкових зарядів 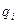, то згідно з принципом суперпозиції, робота сил такого поля над зарядом 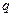буде дорівнювати алгебраїчній сумі робіт сил, зумовлених кожним із зарядів:

,

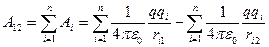потенціальна енергія заряду 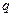в цьому полі

,

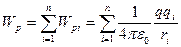потенціал поля систем 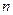точкових зарядів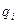

.

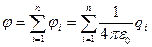При неперервному розподілі зарядів у скінченій області простору з об’ємною густиною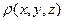

.

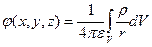На підставі рівняння (1.18) знаходимо, що навколо точкового заряду існує ряд сферичних поверхонь з однаковими потенціалами для кожної окремої поверхні. Такі поверхні називають еквіпотенціальними. Еквіпотенціальні поверхні є і навколо заряджених тіл довільної форми. Взагалі, під еквіпотенціальною поверхнею розуміють поверхню однакових потенціалів, або ж геометричне місце точок з однаковими потенціалами. Тоді, окрім ліній напруженості, поле можна описувати графічно за допомогою еквіпотенціальних поверхонь (рис.1.8).

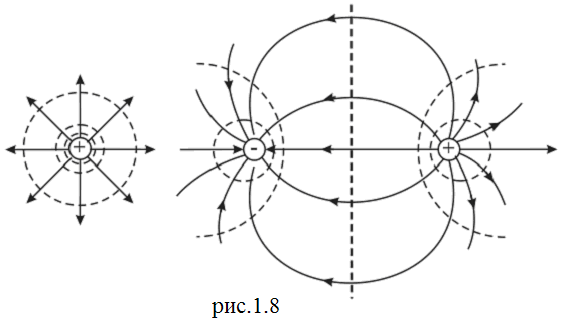
- лінії напруженості поля ,

- сліди розтину еквіпотенціальних поверхонь.

Із рівнянь (1.20) та (1.21) знаходимо, що лінії вектора перпендикулярні до еквіпотенціальних поверхонь. Насправді, при переміщенні заряду 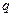по еквіпотенціальній поверхні елементарна робота 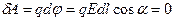. Очевидно, що , .

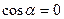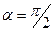1.6. Зв'язок між напруженістю та потенціалом електростатичного поля

Електростатичне поле можна описати або за допомогою векторної величини – напруженості , або за допомогою скалярної величини – потенціалу 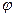цього поля. Очевидно, що між цими характеристиками поля має бути певний зв'язок. Оскільки пропорційна силі, що діє на заряд, а 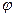- потенціальній енергії заряду, то варто очікувати, що зв'язок між і 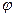має бути аналогічним зв’язку між силою та потенціальною енергією.

Оскільки електростатичне поле є потенціальним, то отримане в механіці [4] співвідношення між силою та потенціальною енергією

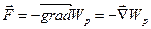(1.22)

є справедливим і в області електрики. Враховуючи співвідношення (1.12) та (1.19), отримаємо:

.

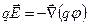Незмінну тут величину 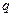можна винести за знак градієнту, що дозволяє скоротити останнє рівняння на цю величину:

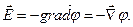(1.23)

Розкривши в (1.23) оператор Набла 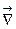, отримаємо:

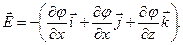(1.24)

Замінивши орти 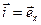, , 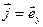, 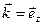рівняння (1.24) запишемо у вигляді:

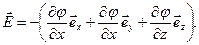(1.25)

В проекціях на координатні осі рівняння (1.24) набирає вигляду:

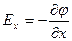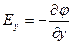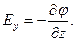, , (1.26)

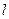Аналогічно проекція вектора на довільний напрям дорівнює взятій з протилежним знаком похідній від 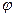по 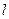, тобто дорівнює швидкості зменшення потенціалу при переміщенні подовж напряму :

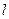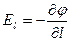. (1.27)

Враховуючи, що 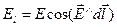, знаходимо, що потенціал поля змінюється найшвидше в напрямі силової лінії.

Впевнимось у справедливості співвідношення (1.24) на прикладі поля точкового заряду. Напруженість поля точкового заряду в певній точці визначається рівнянням (1.10).

Потенціал поля цього ж заряду в тій самій точці

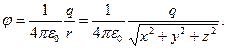
Частинні похідні від цієї функції

,

, ,

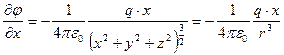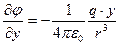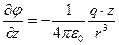Підставимо ці значення в рівняння (1.24):

,

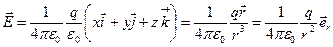що співпадає з (1.10).

1.7. Електричний диполь. Поле диполя

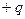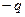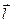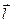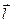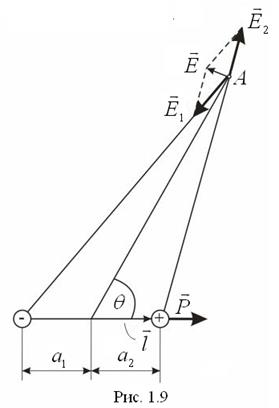
Однією із простих систем точкових зарядів є сукупність двох однакових за абсолютним значенням і протилежних за знаком точкових зарядів і , розміщених на деякій відстані . Таку систему називають електричним диполем. Величину називають плечем (віссю) диполя. Якщо відстань між зарядами не змінюється, то такий диполь називають жорстким. Якщо довжина плеча мала порівняно з відстанню 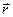від диполя до точки спостереження, то такий диполь називають точковим (рис.1.9). Природним точковим диполем є полярна молекула.

Однією з основних характеристик диполя є електричний дипольний момент 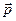− вектор, що чисельно дорівнює добуткові заряду на плече і напрямлений від негативного заряду до позитивного, тобто

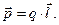(1.28)

Вимірюють електричний дипольний момент в кулон-метрах (Кл·м).

Обчислимо характеристики поля точкового диполя в довільно обраній точці 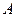(рис.1.9).

За принципом суперпозиції напруженість в точці 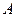дорівнюватиме векторній сумі напруженостей 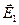і 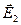полів, створених зарядами 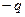та 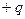. З іншого боку сумарний вектор можна розглядати як векторну cуму двох складових: складову 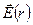, що залежить від відстані між диполем і обраною точкою 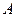, і складову 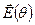, що залежить від кута 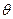орієнтації радіуса – вектора 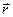: 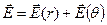. За абсолютним значенням 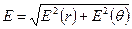. Обчислимо напруженість за абсолютним значенням, скориставшись співвідношенням (1.23). У даному випадку 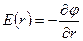, , 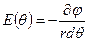де 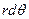- відстань, на яку переміститься кінець радіуса – вектора 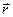(точка 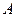) при зміні кута на величину .

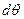Згідно з принципом суперпозиції потенціал поля диполя в точці 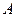буде дорівнювати сумі потенціалів:

.

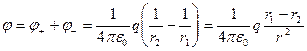Оскільки диполь точковий 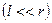, то можна прийняти, що 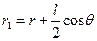, 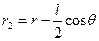. Тоді 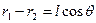, а потенціал поля в точці 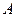буде дорівнювати:

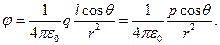(1.29)

Складові напруженості поля та її величина дорівнюють:

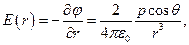(1.30)

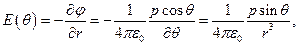(1.31)

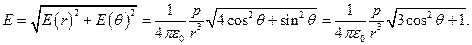(1.32)

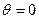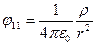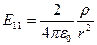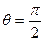На підставі формул (1.29) та (1.32) знаходимо, що при потенціал поля на осі диполя , напруженість ; при потенціал поля на перпендикулярі до диполя 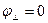; напруженість .

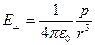Згідно з формулою (1.30) при 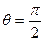проекція 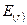дорівнює нулеві, отже вектор 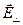паралельний до осі диполя. Згідно з формулою (1.31) при 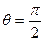проекція 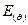позитивна. Це означає, що вектор 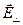спрямований в бік зростання кута 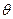, тобто антипаралельно вектору .

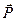1.8. Електричний диполь в однорідному та неоднорідному електричних полях

Розглянемо дію зовнішнього електричного поля на диполь.

Якщо поле однорідне (рис.1.10), то сили, що діють на негативний і позитивний заряди диполя є однаковими за значеннями і протилежними за напрямом, тобто на диполь діє пара сил. Їх рівнодійна дорівнює нулеві. При довільній орієнтації диполя в полі 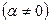на диполь діє обертальний момент

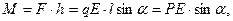, (1.33)

де 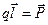(див.(1.28)). У векторній формі вираз (1.33) набирає вигляду

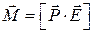. (1.34)

Отже, в однорідному електричному полі пара сил намагається повернути диполь так, щоб кут між векторами 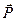і зменшився і диполь встановився в напрямі поля. Можливі два положення рівноваги диполя: диполь паралельний електричному полю (стійка рівновага) і антипаралельний йому (нестійка рівновага).

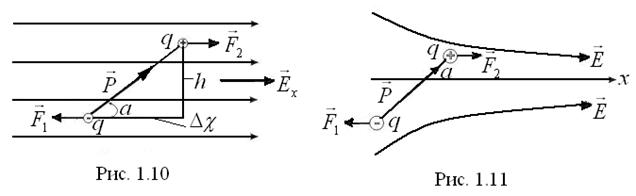
Обчислимо потенціальну енергію диполя в зовнішньому полі. Згідно з формулою (1.19) та принципом суперпозиції ця енергія дорівнює

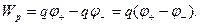(1.35)

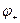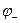Тут і - значення потенціалу зовнішнього поля в тих точках, де знаходяться заряди 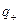і .

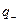Потенціал однорідного поля зменшується лінійно в напрямі вектора . Прийнявши цей напрям за вісь 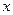(рис.1.10) та враховуючи (1.26),знаходимо, що 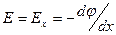. Із рис. 1.10 видно, що різниця 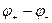дорівнює зміні потенціалу на відрізку :

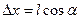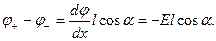
Підставити це значення у формулу (1.35), отримаємо, що

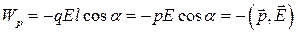. (1.36)

Формула (1.36) не враховує енергію взаємодії між зарядами самого диполя. Досвід свідчить, що формула (1.36) справедлива і в випадку неоднорідного поля.

Якщо поле неоднорідне, то сили 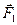і 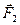за значенням є різними і їхня рівнодійна не дорівнює нулеві. Нехай поле змінюється симетрично осі 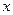, а центр диполя лежить на цій осі (рис.1.11). Прикладом такого поля є поле точкового заряду, якщо вісь 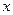− пряма, що проходить через заряд. Згідно з формулою (1.22) знаходимо:

, , .

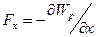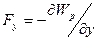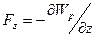Згідно з (1.36), за умови, що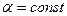

.

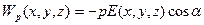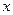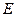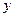Для всіх точок осі похідні за та 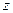дорівнюють нулеві. Таким чином, на диполь діє лише складова 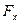. Вона дорівнює

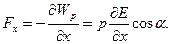(1.37)

Із (1.37) випливає таке: якщо 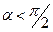, то диполь втягується в область більш сильного поля; якщо 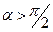, то диполь виштовхується з поля. У випадку несиметричного поля поведінку диполя необхідно розглядати окремо в кожному конкретному випадку.

1.9. Опис властивостей електричного поля

Для опису властивостей векторних полів, в тім числі і електричного, зручно використати математичний апарат – так званий векторний аналіз. Одним із елементів цього аналізу є градієнт, який використовують для скалярних полів. Якщо кожній точці з координатами 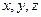співставляється значення скалярної величини 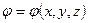, то кажуть, що задано скалярне поле 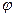. Градієнтом величини 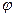називають вектор

.

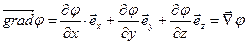Для електростатичного поля 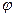- потенціал поля (див.(1.23)-(1.25)).

При зміщенні на відрізок 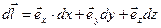зміна функції 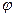дорівнює

.

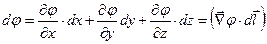Розглянемо деякі інші елементи.

1.9.1. Потік вектора напруженості електричного поля

Скористаємося моделлю текучої рідини. Нехай течія рідини характе- ризується полем вектора швидкості 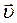. Об’єм 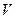рідини, що протікає в оди- ницю часу через деяку уявну поверхню 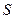, називають потоком рідини через цю поверхню. Очевидно, що за проміжок часу 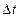через плоску поверхню 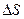протікає об’єм рідини 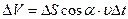(рис.1.12).

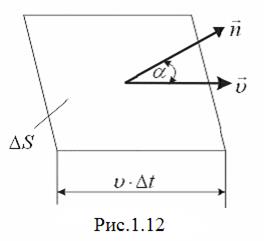
Розділивши цей об’єм на проміжок часу 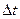, знайдемо потік рідини через поверхню :

.

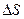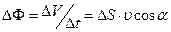Через елементарну поверхню 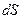довільної форми потік рідини

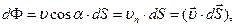(1.38)

де 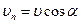- проекція вектора 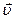на нормаль 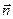, 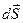- не істинний, а псевдовектор.

Склавши потоки через всі елементарні поверхні, на які була поділена поверхня 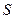, знайдемо потік рідини через всю поверхню :

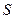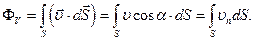(1.39)

Для будь-якого вектора 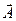величину

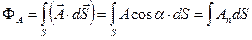(1.40)

називають потоком вектора 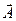через поверхню 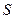. Отже, формула (1.39) описує потік вектора 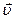через поверхню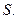

По аналогії з (1.38) – (1.40) для вектора напруженості електричного поля отримаємо:

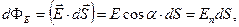(1.41)

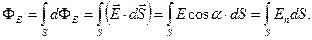(1.42)

1.9.2. Теорема Гаус c а

Німецький вчений Гаусс на початку 19ст. довів, що потік вектора напружено- сті електричного поля через замкнену поверхню пропорційний сумарному заряду під цією поверхнею: 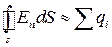(1.43)

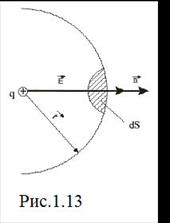
Це твердження називають теоремою Гаусса. Розглянемо цю теорему на прикладі поля точкового заряду, охопленого концентричною сферичною поверхнею радіуса 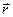(рис.1.13).

Нормаль 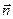до такої поверхні співпадає з радіусом 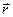. Оскільки поле точкового заряду центральносиметричне , то

.

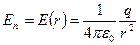Тоді

,

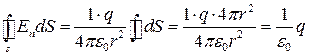що узгоджується з (1.43). Отриманий результат залишається справедливим і для поверхні довільної форми. Насправді, потік вектора через поверхню 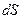(рис.1.14) дорівнює:

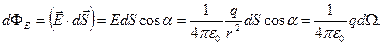
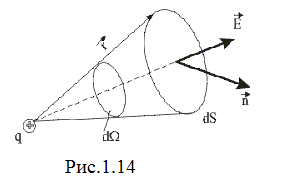Тут 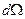- елементарний тілесний кут. Потік через замкнену поверхню

,

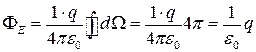що теж узгоджується з теоремою Гаусса.

Якщо під замкненою поверхнею знаходяться 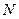точкових зарядів, то згідно з принципом суперпозиції, напруженість поля 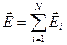.Тому

.

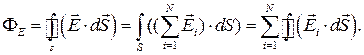Кожен із інтегралів під знаком суми дорівнює 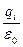. Отже,

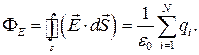(1.44)

У випадку об’ємних 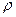і поверхневих 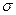безперервно розподілених зарядів формула (1.44) узагальнюється так:

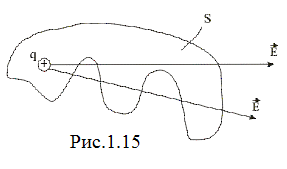
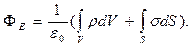(1.45)

В СІ коефіцієнт пропорційності в теоремі Гаусcа дорівнює .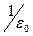

Якщо замкнена поверхня будь-якої форми не охоплює заряди, то 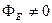, оскільки кожна лінія перетинає поверхню непарне число разів (рис.1.15).

1.9.3. Дивергенція (розходження) вектора

Потік вектора через замкнену поверхню, що відображає принцип суперпозиції, є інтегральною властивістю поля у всьому об’ємі, обмеженому цією поверхнею. Для характеристики поля у будь-якій точці використовують поняття дивергенції вектора .

Якщо потік будь-якого вектора (наприклад вектора швидкості рідини) через замкнену поверхню не дорівнює нулеві, то в об’ємі під поверхнею є джерела або стоки рідини, тобто точки, в яких рідина поступає в об’єм (джерела), або витікає із об’єму (стоки). Величина потоку визначає сумарну потужність джерел і стоків (з загальною назвою джерел).

Відношення потоку до величини об’єму, із якого він витікає, тобто 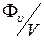дає середню питому потужність джерел, що знаходяться в цьому об’ємі. У векторному аналізі доведено, що границя відношення потоку будь-якого вектора 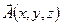, визначеного у всіх точках векторного поля, крізь замкнену поверхню 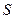до об’єму 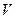, обмеженого цією поверхнею, при 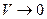(при стягуванні об’єму в точку 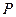) не залежить від форми 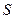. Границя цього відношення визначає дійсну питому потужність джерел в цій точці 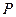. Ця потужність і є характеристикою векторного поля в точці 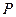. Її називають дивергенцією або розходженням вектора 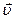і позначають .

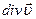Таким чином, за визначенням

.

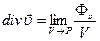Для будь-якого вектора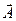

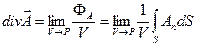. (1.46)

Аналогічно формулі (1.46) дивергенція вектора дорівнює:

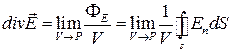. (1.47)

Якщо сумарний заряд під замкнутою поверхнею розподілений з об’ємною густиною 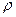, то, згідно з теоремою Гаусса (1.44)

.

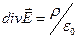Із вище сказаного (див.(1.42), (1.47)) випливає, що і потік і дивергенція є величинами скалярними.

У декартовій системі координат

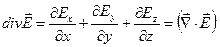(1.48)

1.9.4. Теорема Остроградського–Гаусса

Знаючи дивергенцію будь-якого вектора в кожній точці простору, можна обчислити потік цього вектора через яку завгодно замкнену поверхню обмежених розмірів. Знайдемо його на прикладі рідини з заданим полем швидкості 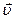. Добуток 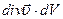дає потужність в об’ємі 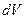. Сума таких добутків, тобто 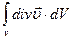дає потужність джерел в об’ємі 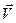. Таким чином отримуємо співвідношення:

.

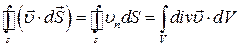Для будь-якого вектора 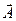маємо:

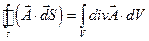. (1.49)

Співвідношення (1.49) називають теоремою Остроградського–Гаусса.

Для електростатичного поля вона набирає вигляду:

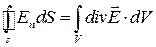. (1.50)

На підставі формул (1.42), (1.48) та (1.50) отримуємо:

.

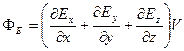1.9.5. Циркуляція вектора

Повернемося знову до течії ідеальної рідини, що не стискається. Уявімо собі замкнену лінію – контур 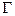. Припустимо, що якимось чином ми миттєво ззаморозимо рідину у всьому об’ємі, за винятком дуже тонкого замкненого каналу постійного перетину 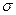, який вміщує в себе контур 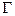(рис. 1.16). В залежності від характеру поля вектора швидкості 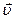рідина в каналі може бу-

ти або нерухомою, або буде 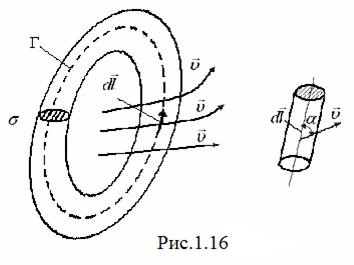ру-

хатися уздовж контуру (циркулювати) в одному із двох можливих напрямів.

Оскільки рідина ідеальна, то дія стінок каналу може змінити лише напрям імпульсу молекули, а взаємодія між молекулами призведе до вирівнювання швидкості між ними. Імпульс частинок рідини в об’ємі каналу, що відповідає його ділянці 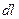, за величиною буде дорівнювати 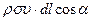, де 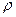– густина рідини, 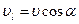– проекція швидкості 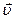на напрям 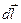. Імпульс рідини у всьому каналі буде дорівнювати

,

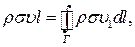де 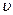– швидкість циркуляції. Скоротивши попередній вираз на 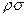, отримаємо, що циркуляція 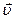по 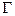дорівнює .

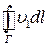Для будь-якого вектора 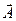циркуляція по довільному контуру :

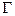циркуляція 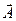по 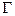дорівнює 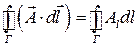(1.51)

Аналогічно визначається циркуляція вектора напруженості електричного поля по довільному контуру :

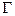циркуляція по 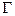дорівнює 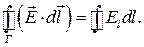(1.52)

У §1.4 було доведено, що для електростатичного поля 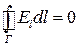. Отже, векторне поле напруженістю є потенціальним, якщо циркуляція вектора по довільному замкненому контуру дорівнює нулеві.