Конституентой нуля называют функцию n аргументов, которая принимает значение, равное нулю только на одном наборе аргументов.
От табличного представления функции легко перейти к ее алгебраическому представлению, причем одну и ту же функцию можно представить в двух формах.
Совершенной дизъюнктивной нормальной формой (СДНФ) функции называют дизъюнкцию конституент единицы, равных единице на тех же наборах, что и заданная функция. Эту форму называют также первой стандартной формой.
Переход от таблицы к СДНФ осуществляют так: для каждого набора, на котором функция равна единице, записывают элементарное произведение всех аргументов, причем если аргумент в этом наборе имеет значение 0, то пишут его отрицание. Затем производят логическое сложение этих элементарных произведений. Эту процедуру называют составлением структурной формулы по единицам. Для функции Y 1 из табл. 2.1 СДНФ имеет вид
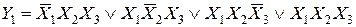 (2.1)
(2.1)
Форма, равная конъюнкции конституент нуля, которые равны нулю на тех же наборах, что и заданная функция, называется совершенной конъюнктивной нормальной формой (СКНФ). Эту форму называют также второй стандартной формой. Переход от таблицы к СКНФ осуществляют так: для каждого набора, на котором функция равна нулю, составляют элементарную логическую сумму (дизъюнкцию) всех аргументов, причем если аргумент в этом наборе принимает значение 1, то пишут его отрицание. Затем эти элементарные суммы объединяют операцией логического умножения. Эту процедуру называют составлением структурной формулы по нулям. Для функции Y 1 из табл. 2.1 СКНФ имеет вид
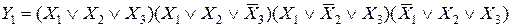 (2.2)
(2.2)
Путем алгебраических преобразований можно перейти от одной формы к другой. При равном числе выражений для минимизации функций более удобна форма СДНФ.
Минимизация (упрощение) булевых функций производится с помощью теорем алгебры логики. Рассмотрим основные теоремы и положения алгебры логики.
Запишем правила выполнения операций ИЛИ и И, расположив строчки в обратном порядке:
| ИЛИ | И |
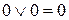
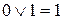
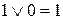
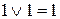
| 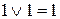
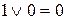
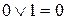
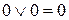
|
Нетрудно видеть, что если заменить в строках ИЛИ и И все 0 на 1, все 1 на 0 и знаки дизъюнкции на знаки конъюнкции, то правила меняются местами: строка ИЛИ превращается в строку И, и наоборот. В этом состоит принцип двойственности, который в общем виде записывается так:
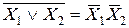 (2.3)
(2.3)
Для преобразования формул алгебры логики с целью их минимизации используются, как и в обычной алгебре, скобки, а если их нет, то сначала выполняется отрицание над отдельными переменными, затем логическое умножение и наконец логическое сложение. Однако если знак инверсии стоит над совокупностью переменных, то он выполняется в последнюю очередь. В процессе преобразования формул используются также теоремы алгебры логики.
Теоремы для одной переменной (легко проверяемые подстановкой X=1 и X=0):
1. 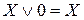
| 4. 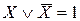
| 7. 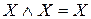
|
2. 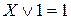
| 5. 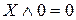
| 8. 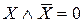
|
3. 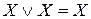
| 6. 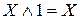
| 9. 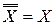
|
Эти теоремы (как и последующие) остаются справедливыми и для случая, если под X понимать не только одну переменную, но и целое выражение.
Теоремы для двух или более переменных:
10. Переместительный закон:
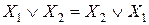 или
или 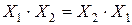 .
.
11. Сочетательный закон:
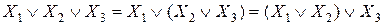 или
или
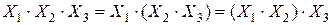 .
.
12. Распределительный закон:
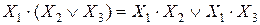 или
или
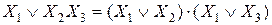 .
.
13. Закон поглощения:
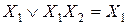 или
или 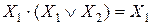 .
.
14. 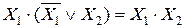 или
или 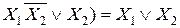 .
.
15. Закон склеивания
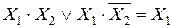 или
или 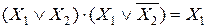 .
.
16. Законы теорема де Моргана
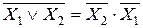 или
или 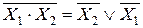 .
.
Наиболее эффективными приемами минимизации являются вынесение за скобки общих членов, а также применение двойного отрицания, теоремы де Моргана, законов поглощения и склеивания. При этом наряду с полным склеиванием часто применяют неполное склеивание, при котором оба члена, участвовавших в склеивании (или один из них), остаются и могут склеиваться с другими членами СДНФ.
Так, используя неполное склеивания четвертой конституенты в (2.1) последовательно с первой, второй и третьей (т.е. сохраняя ее после склеивания), можно привести к виду:
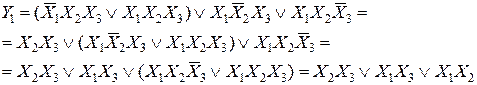
Данную функцию можно реализовать при помощи схемы, представленной на рис. 2.1.
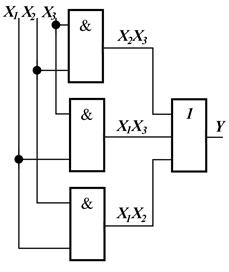
Рисунок 2.1 – Схема, реализующая функцию “голосование по большинству”.
В процессе минимизации используют понятие смежных конституент, которыми называют конституенты, отличающиеся только одним аргументом (в одну конституенту аргумент входит с инверсией, а в другую – без нее).
Две смежные конституенты, склеиваясь, образуют результирующую конъюнкцию с числом аргументов, на единицу меньшим, чем в исходных конституентах, так как в ней отсутствует аргумент, которым отличаются смежные, исходные конституенты. Эту результирующую конъюнкцию называют импликантой .
Количество аргументов в конституенте или импликанте называют рангом. При склеивании ранг результирующей конъюнкции, т.е. импликанты уменьшается на единицу. Так, последнее выражение в (1.2) состоит из трех импликант второго ранга.
Импликанты с одинаковым числом аргументов могут оказаться смежным, и их можно склеить между собой. Так, четыре конституенты четвертого ранга
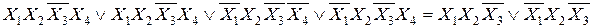
склеиваясь, первая со второй и третья с четвертой, образуют две импликанты третьего ранга, которые могут быть склеены по X 1:
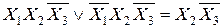 (2.4)
(2.4)
образуя импликанту второго ранга.
Говорят, что импликанта накрывает все конституенты, в результате склеивания которых она получена.
Процесс многоступенчатого склеивания приводит к импликантам, которые не склеиваются с другими членами. Такие импликанты называют простыми. Простые импликанты с конституентами, не имевшими смежных до склеивания, образуют сокращенную дизъюнктивную нормальную форму функции. Однако в некоторых случаях в ней могут содержаться лишние имплика нты, которые могут быть исключены без изменения значения функции.
ДНФ, не содержащая лишних импликант, назвается тупиковой ДНФ. Некоторые функции могут иметь несколько тупиковых форм. Тупиковая функция, содержащая наименьшее количество аргументов, называется минимальной ДНФ.
Использование рассмотренных приемов для нахождения минимальной формы функции требует определенной интуиции и применимо лишь при достаточно простых функциях небольшого числа аргументов. В более сложных случаях (например, при четырех и более аргументах) процесс минимизации целесообразнее алгоритмизировать.
Алгоритмизировать нахождение СДНФ позволяет теорема Квайна: если в совершенной дизъюнктивной нормальной форме функции провести сначала все возможные операции неполного склеивания и затем все возможные операции поглощения, то в результате получится сокращенная дизъюнктивная нормальная форма функции.
Минимизацию по Квайну надо начинать с совершенной ДНФ. Если функция задана в произвольной форме, то производят ее развертывание, умножая член, не содержащий какого либо аргумента, на логическую единицу (теорема 4) и получают два члена, содержащие весь набор аргументов.
Одним из методов отыскания лишних импликант является метод испытания членов: чтобы испытать некоторый член функции, следует исключить его из сокращенной ДНФ и подставить в оставшееся выражение такие значения аргументов, которые обращают исключенный член в единицу. Если при такой подстановке оставшееся выражение окажется тождественно равным единице, то испытываемый член окажется лишним.
Рассмотрим два примера: рассмотрим сокращенную ДНФ
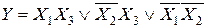 .
.
Испытаем член X1X3, обращенный в 1 при X1 =1 и X3 =1. Подставив в оставшееся выражение 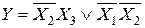 значения X1 =1 и X3 =1, получим
значения X1 =1 и X3 =1, получим
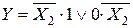 .
.
При X2 =0 последнее выражение равно 1, но при X2 =1 оно не равно 1. Следовательно, член X1X3 не является лишним и его исключить нельзя.
Испытаем член 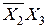 , обращаемый в 1 при X2=0 и X3 =1. Подставив в оставшееся выражение
, обращаемый в 1 при X2=0 и X3 =1. Подставив в оставшееся выражение 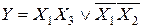 значения X2 =0 и X3 =1, получим
значения X2 =0 и X3 =1, получим
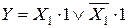 .
.
Последнее выражение равно 1, как при X 1 = 1, так как и при X 1 =0. Значит, член 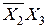 можно опустить и тупиковая форма примет вид
можно опустить и тупиковая форма примет вид
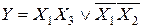 ,
,
являющийся минимальной формой рассматриваемой функции.
3. Описание лабораторной установки
В состав лабораторной установки входят: лабораторная макетная плата, блок питания и контактные перемычки.
4. Порядок выполнения теоретических расчетов
Изучить порядок составления логических функций и теоремы алгебры логики, позволяющие произвести минимизацию функций. Согласно индивидуальному заданию (таблица 2.1), составить таблицу истинности функции для четырех аргументов. Используя СКНФ или СДНФ, составить логическое уравнение для этой функции. Произвести минимизацию функции.
Таблица 2.1 – Варианты индивидуальных заданий
| Вариант | Задание |
| 1 | Функция принимает значение 1, если три любых аргумента (или все) равны 1, и 0 в остальных случаях. |
| 2 | Функция принимает значение 1, если три любых аргумента (или все) равны 0, и 1 в остальных случаях. |
| 3 | Функция принимает значение 1, если аргументы X 1 = X 2 и X 3 = X 4, а в остальных случаях принимает значение 0. |
| 4 | Функция принимает значение 1, если аргументы X 1 ≠ X 2 и X 3 = X 4, а в остальных случаях принимает значение 0. |
| 5 | Функция принимает значение 1, если аргументы X 1 = X 2 и X 3 ≠ X 4, а в остальных случаях принимает значение 0. |
| 6 | Функция принимает значение 1, если аргументы X 1 ≠ X 2 и X 3 ≠ X 4, а в остальных случаях принимает значение 0. |
| 7 | Функция принимает значение 1, если аргументы X 1 = X 3 и X 2 = X 4, а в остальных случаях принимает значение 0. |
| 8 | Функция принимает значение 1, если аргументы X 1 ≠ X 3 и X 2 = X 4, а в остальных случаях принимает значение 0. |
| 9 | Функция принимает значение 1, если аргументы X 1 = X 3 и X 2 ≠ X 4, а в остальных случаях принимает значение 0. |
| 10 | Функция принимает значение 1, если аргументы X 1 ≠ X 3 и X 2 ≠ X 4, а в остальных случаях принимает значение 0. |
| 11 | Функция принимает значение 1, если сумма всех аргументов равна 3 или 4, в остальных случаях принимает значение 0. |
| 12 | Функция принимает значение 1, если аргументы X 1 = X 2 или X 3 = X 4, а в остальных случаях принимает значение 0. |
| 13 | Функция принимает значение 1, если аргументы X 1 ≠ X 2 или X 3 = X 4, а в остальных случаях принимает значение 0. |
| 14 | Функция принимает значение 1, если сумма всех аргументов не равна 3, в остальных случаях принимает значение 0. |
| 15 | Функция принимает значение 1, если аргументы X 1 = X 2 или X 3 ≠ X 4, а в остальных случаях принимает значение 0. |
| 16 | Функция принимает значение 1, если аргументы X 1 ≠ X 2 или X 3 ≠ X 4, а в остальных случаях принимает значение 0. |
| 17 | Функция принимает значение 1, если сумма X 1 и X 2 больше суммы X 3 и X 4, в остальных случаях принимает значение 0. |
| 18 | Функция принимает значение 1, если сумма X 1 и X 2 меньше суммы X 3 и X 4, в остальных случаях принимает значение 0. |
| 19 | Функция принимает значение 1, если X 1 и X 4 принимают одинаковое значение, в остальных случаях принимает значение 0. |
| 20 | Функция принимает значение 1, если X 1 и X 4 принимают разное значение, в остальных случаях принимает значение 0. |
5. Порядок выполнения экспериментальных исследований
1. Разработать принципиальную схему, реализующую минимизированную логическую функцию.
2. На лабораторном стенде собрать с помощью контактных перемычек схему для исследования заданной логической функции.
3. Построить таблицу истинности для логической функции исследуемой логической функции. Состояние входов и выхода определяется при помощи светодиодов.
4. Сравнить полученную в результате эксперимента таблицу истинности с таблицей, полученной теоретическим путем.
6. Содержание отчета
1. Цель работы.
2. Задание, таблицу истинности в соответствии с заданием.
3. Логическое выражение по таблице истинности на основе СКНФ или СДНФ, минимизацию логического выражения.
4. Принципиальная схема, реализующая логическое выражение.
5. Таблицы истинности по результатам эксперимента.
6. Выводы по работе.
7. Контрольные вопросы
1. Как составить СКНФ по таблице истинности?
2. Как составить СДНФ по таблице истинности?
3. Какие основные теоремы алгебры логики известны Вам?
4. Сформулируйте теорему Квайна.
5. В чем заключается метод испытания членов логического выражения?
Библиографический список
1. Хоровиц П. Искусство схемотехники : пер. с англ. – 6-е изд., перераб. / П. Хоровиц, У. Хилл. – М. : Мир, 2001. – 704 с.
2. Бродин В.Б. Системы на микроконтроллерах и БИС программируемой логики / В.Б. Бродин, А.В. Калинин. – М. : ЭКОМ, 2002. – 400 с.
3. Угрюмов Е.П. Цифровая схемотехника : учебное пособие / Е.П. Угрюмов. – Спб. : BHV-Санкт-Петербург, 2004. – 782 с.
4. Мышляева И.М. Цифровая схемотехника: учебник / И.М. Мышляева. – М.: Академия, 2005. – 400 с.
5. Опадчий Ю.Ф. Аналоговая и цифровая электроника. Полный курс : учебник для вузов / Ю.Ф. Опадчий, О.П. Глудкин, А.И. Гуров. – М.: Горячая линия Телеком, Радио и связь, 2005. – 768 с.
Заказ №______ от “____” ______________2013. Тираж_____ экз.
Изд–во СевНТУ








