Применение диакоптики к расчету нелинейных электрических цепей переменного тока с учетом высших гармоник
§ П10.1. Основные положения метода. Напомним, что под диакоптикой понимают расчет сложных схем по частям с последующим согласованием решений и получением решения для схемы в целом. Методы применения диакоптики для расчета сложных разветвленных нелинейных цепей постоянного тока были изложены в § 13.15. Здесь применим ее к расчету цепей переменного тока с учетом высших гармоник.
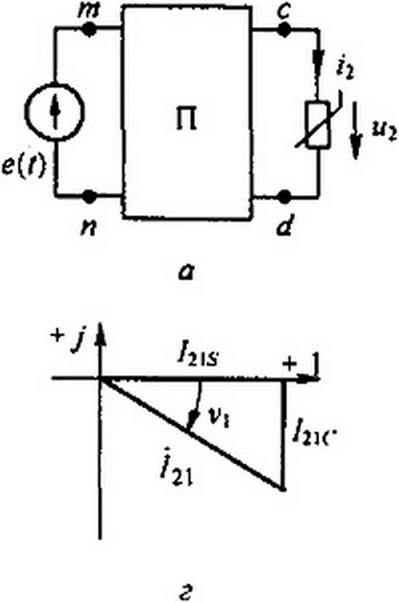
На рис. П10.1, а изображена обобщенная электрическая цепь, состоящая из линейной и нелинейной частей. Линейная часть представлена линейным пассивным четырехполюсником, содержащим элементы с сосредоточенными или распределенными параметрами {или и с теми, и с другими), нелинейная часть — нелинейным, либо резистивным, либо индуктивным, либо емкостным элементом с симметричной, соответственно, вольт-амперной, всбер-амперной или кулон-вольтной характеристикой. На входе четырехполюсника (зажимы тп) действует синусоидальная ЭДС е(/), на выходе нелинейный элемент.
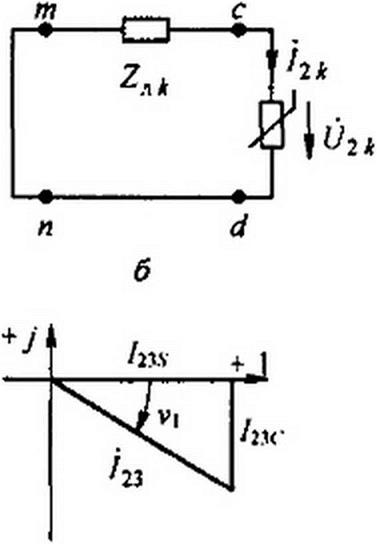
Нелинейная и линейная части схемы соединены в точках с и d. Напряжение ucJ и ток /2 являются общими для обеих частей схемы. В напряжении и в токе в установившемся режиме содержатся в общем случае первая и высшие гармоники. Так как ЭДС на входе схемы не содержит высших гармоник, то для любой высшей (А) гармоники {к * 1) схема замещения может быть представлена (см. рис. П 10.1, о) в виде последовательного соединения нелинейного элемента, комплексную амплитуду напряжения А-гармоники на котором обозначим t/2i, атока /2*, и входного сопротивления Znk на А-й гармонике линейного четырехполюсника по отношению к зажимам cd при коротком замыкании на зажимах тп (рис. П10.1, б). Сумма падений напряжений по контуру равна нулю:
+/2, = 0. (П10.1)
Из уравнения (П10.1) следуют два основных соотношения, положенных в основу согласования решений для линейной и нелинейной частей по высшим гармоникам:
1) модули напряжений U2k и 4* ^л* для любой А*1 гармоники должны быть равны;
2) аргументы этих комплексов должны отличаться на ±180 .
 |  |  | |||||||
 | |||||||||
 | |||||||||
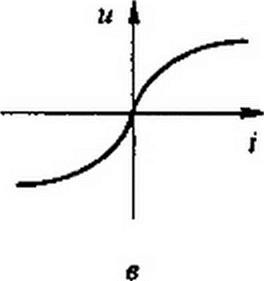
§ ПЮ.2. Вывод расчетных формул связи гармоник напряжений и токов разных частот с углом у3, Идею метода поясним на примере расчета цепи (см. рис. П 10.1, а) с учетом первой и третьей гармоник, взяв в качестве нелинейного элемента резистор с симметричной вольт-амперной характеристикой (рис. П 10.1, в), описываемой гиперболическим синусом
z = ashPu. (ПЮ.2)
Будем считать известными для четырехполюсника его А-маггрицу по первой гармони-
 | |||||||||||
 |  | ||||||||||
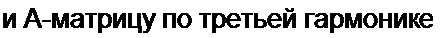 |  | ||||||||||
 | |||||||||||
нейшем будут иметь по два или по три индекса. Первый слева индекс (цифры 1 или 2) будет свидетельствовать: ко входу (I) или к выходу (2) четырехполюсника относится эта величина. Второй по порядку индекс: если равен I, то соответствует 1 гармонике, а если 3 — третьей. Третий индекс: если 5, то речь идет о синусоидальной компоненте, а если С— косинусоидальной. Для сокращения записи (уменьшения числа индексов) индекс амплитуды т ставить не будем.
Напряжение на выходе четырехполюсника обозначим и2 и примем его равным
 «2 = Un sin cor + U23 sin(3cor + у3).
«2 = Un sin cor + U23 sin(3cor + у3).
Здесь {/2| — амплитуда первой, a U22 — третьей гармоники.
Подставим (П10.3) в (П10.2) и, воспользовавшись формулами § 15.16, запишем ток /2 на выходе четырехполюсника через бесселевы функции от мнимых аргументов jx = j^U2i и yy = JpC/23-
‘2 ~ ^21Х sin<01 + /2|С COSO)/ + /2J5 sin 3(0/ + /2Jt- cos 3 со/. (П10.4)
Индекс 215 свидетельствует (читая с конца), что это амплитуда, соответственно, синусной компоненты первой гармоники тока на выходе четырехполюсника. Амплитуды токов равны
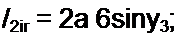 | |||||||||||||||
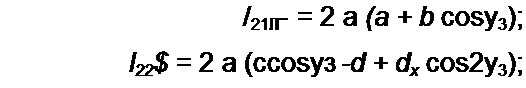 | |||||||||||||||
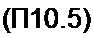 | |||||||||||||||
 | |||||||||||||||
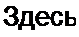 | |||||||||||||||
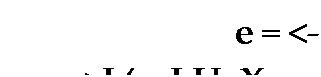 | |||||||||||||||
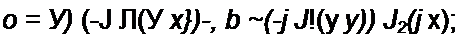 | |||||||||||||||
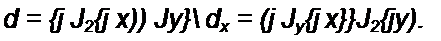 | |||||||||||||||
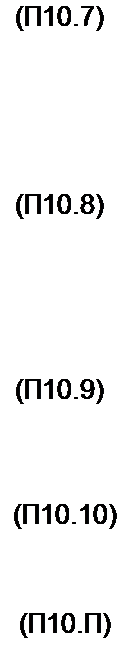
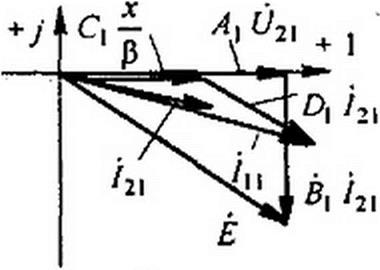
Комплексная амплитуда первой гармоники тока /2 (см. рис. П10.1, г)
121 = 2 a а 71 + + 2 fx cosy3:;
b sin Уз Л sin уз
V) = arctg—L -■ 3 = arctg—
a + ocosy3 a + /| cosy3
Здесь
f -_b = <~J hU J x>
a ^o(;»(-jJ|(yx))'
Комплексная амплитуда третьей гармоники тока i2 (см. рис. П10.1, d);
/23 = /23 е7
, _ _ sin уз + A sin2ys
/23 = 2 а с F4 ■ v3 = arctg------------------------------------------ -3-.-J .----------------------- .
cos Уз -/} + /2 cos2y3
f .
2 c (-j y))J0(j x)’
f - d -
3 C Jq(jx)(-j J}(j y)'
Таблица П10.1
| Функция | X | У | ||||
| I | 1.6 | 2 | 2,6 | 3 | ||
| 4 | - 0,292 | - 0,406 | - 0,459 | -0,511 | -0,5326 | |
| 5 | -0,319 | - 0.4436 | -0,501 | - 0,559 | - 0,582 | |
| 6 | - 0,339 | - 0,470 | - 0,536 | - 0,593 | -0,617 | |
| 4 | - 0,0739 | -0,1064 | -0,1283 | -0,153 | -0,1977 | |
| л | 5 | - 0,09447 | -0,136 | -0,164 | -0,196 | -0,214 |
| 6 | -0,1124 | -0.1613 | -0,194 | - 0,232 | - 0,254 | |
| 4 | 0,6659 | 0,479 | 0,422 | 0,380 | 0,364 | |
| h | 5 | 0,8536 | 0,6146 | 0,544 | 0,488 | 0,467 |
| 6 | 1,088 | 0,725 | 0,642 | 0,576 | 0,551 | |
Функция
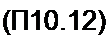 F4 = 7(C0StPj ~/3 + Л cos2y3)2 + (sin\p3 + /2 sin2ц/3)2 =
F4 = 7(C0StPj ~/3 + Л cos2y3)2 + (sin\p3 + /2 sin2ц/3)2 =
= tfl + Z? +/з +2Л cosvp3 -2/3 (cos^j +/2 cos2v3).
Значения функций /2, /3 для ряда значений х и у представлены в табл. ПЮ.1.
Рассмотрим соотношения в схеме рис. П10.1, а. полагая величины х = 0(/2| и у = 01/23 известными. Для схемы замещения по третьей гармонике {рис. П10.1, а) составим уравнение по второму закону Кирхгофа:
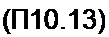 ^23 +2лз /2з ~0-
^23 +2лз /2з ~0-
Здесь 2л3 = В3 / А3 = хл3 е?ч>л'— входное сопротивление четырехполюсника по третьей гармонике по отношению к зажимам cd при коротком замыкании на зажимах тп\ В3
 | |||
 | |||
Уравнение (П10.13) свидетельствует, что нелинейный резистор преобразует часть энергии, получаемой им от источника ЭДС на входе схемы на частоте о, в энергию на частоте 3 со, восполняя потери энергии на частоте 3 © в линейном сопротивлении 2л3 и создавая реактивную мощность на третьей гармонике в цепи, влияя при этом на модуль и аргумент первой гармоники тока и напряжения на входе четырехполюсника.
§ ШО-3. Определение угла цг3 при резистивном нелинейном элементе ня выходе четырехполюсника. Составим уравнение для мгновенных значений тока и напряжений по второму закону Кирхгофа для контура третьей гармоники рис. П 10.1, а, эквивалентное уравнению (П10.13) для комплексных величие, сначала для сопротивления
Z„3 = R3 - . а затем для Z 3 = R3 + /3 w L, используя формулы (П10.4)-(П10.6),
3 и С
(П10.9НП10.12).
Продифференцируем уравнение (П10.9) по времени и поделим полученное выражение на Зш:
U23 (cosЗин cos\y3 -sin3w/ sinц/3) + Я3(/235 co$3w/ + /23Г cos3©r) +
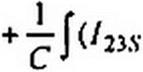
|
(П10.14)
Приравняем нулю сначала синусные, а затем косинусные компоненты этого уравнения и изменим у них знаки на противоположные:
*з бзе ~у— у /23S =“^2з s«n ц/3; - /?3 /2з$’•у—7/2зг =^23 со$у3.
3 © С Зое
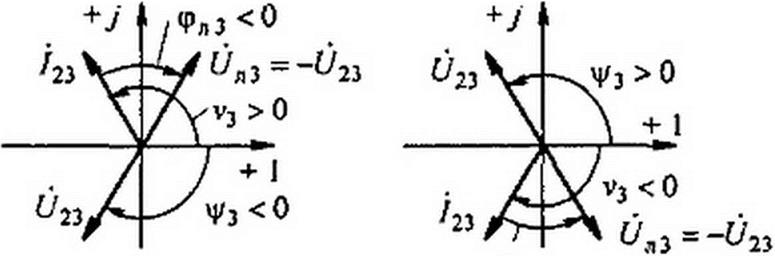 |
|
Рис. П10.2
Возведем эти два уравнение в квадрат и сложим:
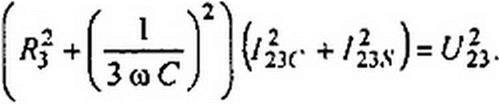 |
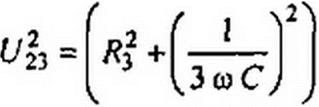 Учтем, что /23С + = (2ас)2 F% (см. формулу (П10.12)). Получим (2 а с)2 (1+Л2+/з2+2/2 cosVj-2/з (cos4/3 + /2 cos2v3)).(ni0.15)
Учтем, что /23С + = (2ас)2 F% (см. формулу (П10.12)). Получим (2 а с)2 (1+Л2+/з2+2/2 cosVj-2/з (cos4/3 + /2 cos2v3)).(ni0.15)
Проделав аналогичные выкладки для Zn3 = /?3 + j 3<о L, получим
(У23 =(/?32 +(3o>L)2)(2ac)2 (1 + /22 + /з2 + 2 /2 cosy3 -2/3 (cosy3 + /2 cos2y3)). (П10.16)
Формулы (П10.15) и (П10.16) тождественны, они позволяют определить угол v3, полагая, что значения R-,, —-—, 3w£, а, 0, х. у известны.
ЗшС
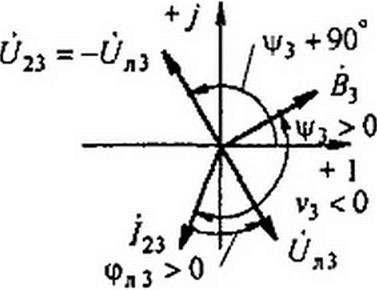
Так как косинус функция четкая, то каждое из уравнений имеет формально по два решения (±4/3), но удовлетворять физике процесса при емкостном характере 7й3 будет Уз <0, а при индуктивном характере Zn3 у3 >0.
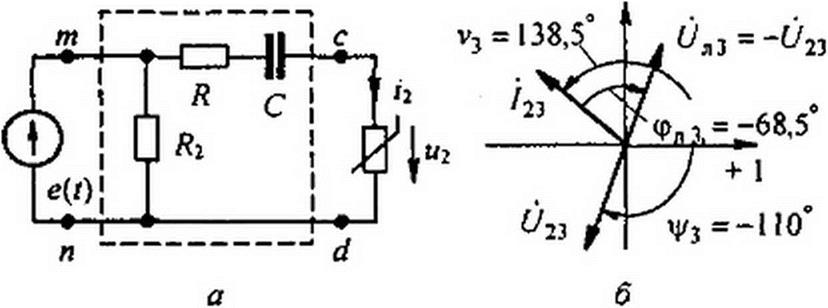
На рис. П10.2, а и б качественно представлены векторные диаграммы по третьей гармонике при резистивном нелинейном элементе на выходе четырехполюсника: на рис. ПЮ.2, а при емкостном характере Zt3, а на рис. П 10.2, б при индуктивном. На диаграммах показаны векторы U23, Uni, /23, углы у3, v3, фл3 и знаки этих углов.
Составим теперь уравнения, подобные уравнениям (П10.15) и (П10.16), когда вместо нелинейного резистора на выходе четырехполюсника будет нелинейная индуктивность.
§ П10.4. Определение угля у3 при нелинейной индуктивности на выходе четырехполюсника. Положим, что зависимость магнитного поля Н в ферромагнитном сердечнике от магнитной индукции 8 описана формулой Н =а} sh 0] В. В индукции учтем первую и третью гармоники В = В{ sin со / + В3 sin(3w/ + ц/3). Площадь поперечного сечения магнитопровода обозначим 5. длину средней магнитной линии — /, число витков катушки — tv. Обозначим Х| = 0, и у, = 0t В3. Тогда напряжение на выходе четырехполюсника
 со tv S 3 со 5v S .и, ,
со tv S 3 со 5v S .и, ,
и2 = — ------ *| COSCO/ + —-------------------- у, cos(3 (О I + у3),
а ток
2 у
i2 =------- — («а + 6 cosy}) sin о/ - 6sin у3 cos<o/) +
 |
w
w
Формула для тока (П 10.18) тождественна формуле для тока (П10.4) в случае нелинейного резистора, если в последней а заменить на ^а' Формулы для (П10.5), (П10.7), IV
 |
|
 |
|
Рис. П10.3
(ПЮ.9) тоже будут применимы, формулы для функций /2, Уз» останутся без изменений. Различие будет в том. что напряжения первой и третьей гармоник будут теперь косинусоидальными, а не синусоидальными функциями времени. Заметим, что угол ф3 будет теперь в аргументе В3, а аргументом U23 будет (90’+ф3).
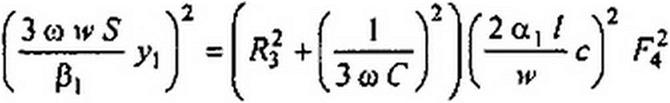 Проделав выкладки, аналогичные выполненным в § П10.3, получим уравнение
Проделав выкладки, аналогичные выполненным в § П10.3, получим уравнение
(при Z„ = i-); (П10.19)
3 со С
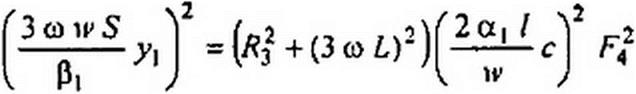 и уравнение
и уравнение
(при Zni - R3 + ;3со£). (П 10.20)
Как и в случае резистивного нелинейного сопротивления, уравнения (ПЮ. 19) и (П10.20) будут давать по два решения ( +ф3 и -ц/3). Теперь углу фл3 >0 соответствует ц/3 >0 и углу фл3 <0 соответствует ф3 <0.
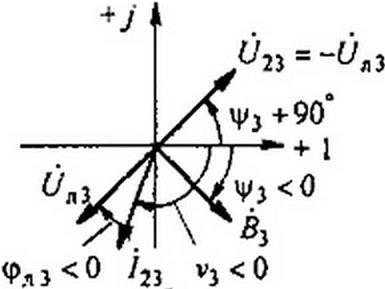
На рис. П10.3, а качественно показано взаимное расположение векторов В3 = By еу 623 = (/23 е>(9О*ч'з). 0п3, /23 = /23 е7’\ углы ф3>0, v3<0 при Флз>0» а на рис. ПЮ.З, б — при фдз < 0. В обоих случаях выполнено условие U23 = -l23 Zn3.
При Фл3 >0 угол v3<0 подсчитан по формуле (П 10.9) при ф3<0, а при Фл3<0 угол v3 < 0 подсчитывается по формуле (П10.9) в зависимости от величины угла фл3 при Ф3 > 0 или при ф3 < 0.
§ П10.5. Определение утла ф3 при нелинейном конденсаторе на выходе четырехполюсника. Кулон-вольтную характеристику конденсатора опишем формулой иг = а2 $hp2<?• Положим, что заряд q = Ci sinco/ + Q3 sin(3co/ + ф3). Теперь угол ф3 представляет собой аргумент третьей гармоники заряда. Обозначим х2 = 02 Q\ и Уг = 02 Qj и определим напряжение на выходе четырехполюсника:
и2 - Uc ~ + ^2ir cosco/ + (723s. sin3cof + U23C cos3co/. (П10.21)
Амплитуды напряжений U2\s> ^2U'' UiJS' k'23(- в последнем выражении определяются так же, как определялись амплитуды токов /2|.у, /2И-, /23,?, /23Г в § П10.2 по формулам (П10.5) и (П10.6) с тем отличием, что а, х и у в этих формулах надо будет заменить, соответственно, на а2, х2 и у2. Справедливы будут и формулы (П10.7)-(П10.10), (П10.12). (П10.13), если в них сделать замену а, х и у на а2. х2 и у2 и определять по ним не /21, vt, /23, v3, а (72), у', (А3, v3.
 Мгновенное значение тока /2 теперь будет
Мгновенное значение тока /2 теперь будет
= co Q} cosco/ + 3 co cos(3co/ + ф3) = ~ x2 cosco/ + — y2 cos(3co/ + y3) = 0. 02 02
Составим уравнение по второму закону Кирхгофа для схемы замещения на третьей гармонике при индуктивном характере сопротивления 2л3 = R3 +j 3 со L:
(/23s- sinco/ + t/23f cos3co/ + R3 cos(3co/ + ф3)+ £3— ------------------------------------------------------------------------- y-> cos(3<o/ + ф3) = 0.
P? J
После небольших преобразований» подобных проделанным в § П 10.3 и П10.4, получим уравнение для определения угла
/ . \2
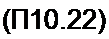 (2а2с)2Г42 = у2 (/?2+ (3со Д)2).
(2а2с)2Г42 = у2 (/?2+ (3со Д)2).
X Р2 J
Теперь функция F% оказалась в левой части формулы (П 10.22), а не в правой, как это было в двух предыдущих параграфах (Г4 по-прежнему определяется формулой (П10.12)). Теперь vj —это аргумент напряжения {/2J=c/23 анетока /23 = /23eyv-'.
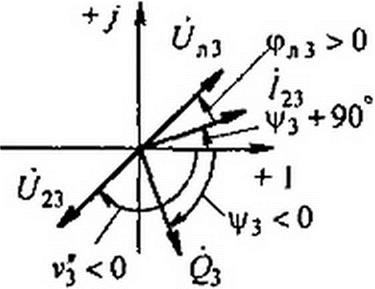
По-прежнему из двух формально возможных решений
|
для угла физике процесса будет соответствовать только одно решение (в рассматриваемом случае при <ря3 > 0 значение Уз < 0).
На рис. П10.4 качественно построена векторная диа
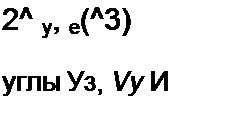 грамма, на которой изображены векторы амплитуд третьей
грамма, на которой изображены векторы амплитуд третьей
гармоники заряда Qyt^3. тока /23 напряжения (У23 = д/д/гз.У +^23С е7‘\
направления их отсчета при ул3 >0, соблюдая условие й2з=-4/я3.
§ П10.6. Последовательность расчета цепи с учетом третьей гармоники при известном несинусоидальном напряжении на выходе четырехполюсника. Последовательность расчета рассмотрим на примере. Схема четырехполюсника представлена на рис. П10.5, а. В ней R = 1,576 Ом, С = 1,325 мкФ, /?2 -20 Ом. Частота f = Ю4 Гц. Вольт-амперная характеристика резистора описана формулой i - a shpw. коэффициенты а = 0,0122 А, р = 0,4 В’1.
Решение. Подсчитываем сопротивление конденсатора на частоте первой и третьей гармоник:
—— = 12 Ом и —-— = 4 Ом. со С 3<о С
По формулам § 4.5 находим коэффициенты A-матриц на частоте первой и третьей гар
моник:
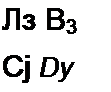 | |||||||
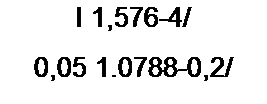 | |||||||
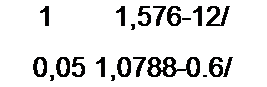 | |||||||
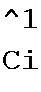 | |||||||
Определяем входное сопротивление четырехполюсника со стороны зажимов cd при коротком замыкании зажимов тп:
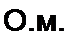 Z, j = -^- = 1,576 - 4 / = 4.3 е*7 68S’
Z, j = -^- = 1,576 - 4 / = 4.3 е*7 68S’
Полагаем и2 = 12,5 sin о/ + 2,5 sin(3o/ + у3).
Определяем х = р12,5 = 5 и у = р-2,5 = 1.
| ||||
| ||||
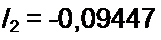
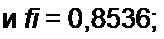 Подсчитываем слагаемые формулы (ПЮ.15).
Подсчитываем слагаемые формулы (ПЮ.15).
При х = 5 и у=] из табл. П 10.1 определяем = 2,52 = 6,25; R} +| —~ I = 4,32 = 18,4875.
I 3 co C J
По формуле (П10.6) коэффициент
с = (-У JyU у)} JO(J х) = 0,56-27,29 = 15,28;
2 а с = 2-0,0122-15,28 = 0,3729; (2ас)2 =0,139.
1+/22 + /32 + 2 /2 cosц/3 -2 /3 (cosУз + /2 со$2ф3) = 1,7375-1,896 cosц/3 +0,1613 cos2\у3.
Подставляем числовые значения всех перечисленных величин в уравнение (ПЮ.15):
6,25 = 2,558 (1,7375 -1,896 cos 4» 3 + 0,1613 cos 2 ц/3)
и определяем из него угол ц/3, задаваясь несколькими его значениями. Путем интерполяции получаем ц/3 =±110°.
Так как Zni имеет емкостной характер, то в соответствии с рис. Л 10.2, а аргумент U2J принимаем равным ц/3=-110.
Записываем напряжение на выходе четырехполюсника:
и2 = 12,5 sin со/ + 2,5 stn(co/ -110 ) В.
Определяем модуль и аргумент тока /23 - 12У е^‘\ полагая при подсчете в соответ ствии с векторной диаграммой в формулах для угла v3 и модуля /23, что ц/3 = +110 :
sin 110°-0,09447 sin 220° ,,о .
v - arclg--------------------------------------------------------- =138,5 ;
cosllO -0,8536-0,09447cos220
J2i=2acF4 = 0,3729 V1 + /22 + /32 +2/2 cos! 10° -2/3(cos110’ + /2cos220°) = 0,581 А;
/23 = 0.581 е'1385’ А.
Напряжение на линейном сопротивлении
On3 =za3 /23 =4,Зе'у68Л° -0,581 е'|38>5* = 2.5ey68S’ В.
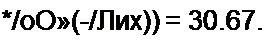 |
Определяем комплексную амплитуду тока /2( первой гармоники на выходе четырехполюсника, имея в виду, что при х= 5 и>= 1 функция j\ = -0,319, а коэффициент а по формуле (П10.6) равен
По формуле (П10.7)
-0,3)9sinJ 10° , о
у. -arcig---------------------------- = -18,5 ;
1 -0,319-cosl 10
/21 = 2 а о J1 + /|2 + 2 cos ц/ з = 2 • 0,0122 • 30,69 • 1,149 = 0,8517;
/21 * 0.86 е“',м’ А.
Комплексную амплитуду ЭДС на входе четырехполюсника определим по уравнению ч еты рехпо л юсн и ка:
E = At (/21 +5i Ап =1— + 0,576-12у)-0.8-е"’18,5' = 14,66 е">4415’ В.
0,4
Комплексная амплитуда тока на входе четырехполюсника
Pl
= 0.05- А-+ (1,0788- j 0.6)- 0.86 е-7’85’ = 1,602-e’J 23 7S’ A.
Зная напряжения и токи первой и третьей гармоник на входе и выходе четырехполюсника, по законам Кирхгофа можно определить ток и напряжение любой ветви четырехполюсника.
Активная и реактивная мощности на входе
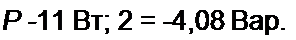 5 = (cos £ /|) + у sin А /ц) = 11-J 4,08;
5 = (cos £ /|) + у sin А /ц) = 11-J 4,08;
Векторные диаграммы для третьей и первой гармоник даны на рис. П10.5, бив.
В заключение отметим, что аналогичным путем можно было бы учесть в расчете и пятую гармонику. С этой целью в случае резистивного нелинейного сопротивления в правую часть формулы (П10.3) следовало бы добавить слагаемое U2S sin(5(i)/ + ф5), вывести новые формулы для первой, третьей и пятой гармоник тока, более полные формулы для функций /|, /2, /з, новые формулы для модулей и аргументов комплексов токов
§ П10.7. Последовательность расчета цепи (рис. П10.1, а) с учетом третьей гармоники при известной синусоидальной ЭДС на входе Ё= Сначала по схеме рис. ГП 0.6, а определим напряжение первой гармоники на выходе четырехполюсника при £
холостом ходе на зажимах cd Ucd х = — и подсчитаем входное сопротивление четырех полюсника по первой гармонике по отношению к зажимам cd при коротком замыкании на зажимах тп (рис. П10.6, б)
= ~г = ^е-т- + J 1m—.
Л] Л) А,
Для схемы рис. П 10.6, в запишем уравнение в комплексах для определения величины х без учета третьей гармоники (полагая здесь для определенности, что на выходе четырехполюсника резистивный нелинейный элемент):
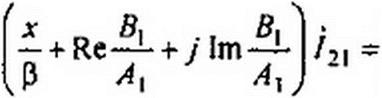 | |||
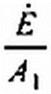 | |||
|
Здесь
/2, =2a(-/Ji(Jx)); y = arg£.
Выделим в этом уравнении действительную и мнимую части:
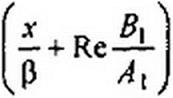 |
|
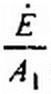 | |||
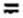 | |||
|
 | |||
 | |||
|
Возведем их в квадрат и сложим для устранения угла (у-фЛ|).
 | |||
 | |||
|
 |
Получим трансцендентное уравнение относительно х:
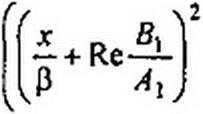 | |||
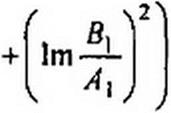 |
|
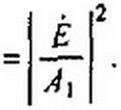 |
|
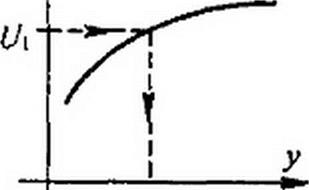
После подсчета величины х можно приступить к определению величины у. С этой целью зададимся диапазоном значений у. Этот диапазон в общем случае зависит от того, является ли нелинейный элемент резистивным, индуктивным или емкостным, от степени насыщения нелинейного элемента и от возможности возникновения в цели резонанса напряжения на третьей гармонике в НЭ и в четырехполюснике, или от резонанса токов в четырехполюснике.
В случае резистивного НЭ и при значении х = 5 зададимся значениями у, равными 1,1,6 и 2, и, подобно тому, как это сделано ранее в § П10.6, подсчитаем значение входного напряжения схемы Для трех случаев, когда х 5, у = 1; х “ 5, у ~ 1,6; х = 5, у = 2. По результатам подсчета построим вспомогательный график зависимости модуля входного напряжения 4/] от величины у (см. рис. Ш0.7). Чтобы определить значение у, отложим по оси ординат этого рисунка величину модуля ЭДС на входе цепи и проведем горизонталь. Точка пересечения этой горизонтали с Ut = f (у) даст искомое значе- ниеу.
Если значение напряжения U} при подсчитанном х и всех трех выбранных значениях у будет превышать величину модуля ЭДС на входе, то это будет свидетельствовать о том. что следует несколько уменьшить х и при тех же значениях у провести новые расчеты.
Приложение ПН








