Причины возникновения странных аттракторов в нелинейных электрических цепях переменного тока
Странные аттракторы — обобщенное наименование непериодических для мгновенных значений величин странных колебаний, возникающих в различных физических системах (в нашем случае электрических) под воздействием периодической вынуждающей силы. В литературе (да н в данной книге тоже) их называют по-разному, например, непериодические, или многопериодические, почти периодические колебания, автомодуляция, хаос, динамический хаос, стохастические колебания и т. п. Но наиболее подходящим обобщающим наименованием для них является, по-видимому, «странные аттракторы». В настоящем Приложении показано, какие физические явления лежат в основе (являются причиной) возникновения различных типов странных аттракторов, как подойти к определению параметров электрических схем, при которых эти колебания возникают, а также вопросы устойчивости странных аттракторов при нелинейных элементах схем различной физической природы. Частично эти вопросы применительно к нелинейному емкостному элементу рассматривались в § 15.71. Но начнем с сопоставления странных аттракторов с наиболее известным и близким к ним типом колебаний — с автоколебаниями.
§ П9.1. Сопоставления автоколебаний (АК) в электрических пенях с источниками постоянной ЭДС и странных аттракторов (СА) в электрических цепях с синусоидальными источниками ЭДС. Каналы действия нелинейной неявно выраженной обратной связи. Между двумя разновидностями колебательных процессов СА, с одной стороны, и АК, с другой, есть сходство, но, однако, значительно больше существенных различий.
Напомним, что для возникновения и устойчивого существования АК-процессов — процессов периодических — необходимо:
1) наличие в схеме источника постоянной ЭДС или тока, нелинейного элемента и обратной связи;
2) в АК-системах релаксационного типа используют нелинейный резистивный элемент, который имеет ВАХ S- или //-образной формы (см. рис. 17.3. б и 17.6, б}, и в схеме должен быть один накопитель энергии (L или Q. Для возбуждения колебаний параметры схемы выбирают так, чтобы изображающая точка оказалась на падающем участке ВАХ НЭ. Обратная связь в рассмотренных в книге примерах проявлялась в том, что напряжение на НЭ управляло процессом зажигания и гашения неоновой лампы в схеме на рис. 17.3, б или процессом прямого и обратного скачка тока в схеме на рис. 17.6, а с туннельным диодом;
3) при автоколебаниях почти гармонического типа в схемах должен быть управляемый нелинейный резистивный элемент и два накопителя энергии (обычно £ и С). В этом случае на ВАХ НЭ, взятого отдельно от схемы, падающий участок отсутствует, а неустойчивость создается явно выраженной электрической или магнитной обратной связью (см., например, рис. 16.5, пример 164);
4) в АК-системах. дающих напряжение на выходе в виде меандра (§ 15.56), элементная база иная: нелинейный индуктивный элемент и два транзистора. В них линейные элементы L и С отсутствуют. Период колебаний определяется временем перемагничивания сердечника нелинейной индуктивности, а обратная связь проявляется в том, что процесс перемагничивания сердечника управляет работой транзисторов.
Теперь перечислим условия, при соблюдении которых в нелинейных цепях переменного тока могут возникать и устойчиво существовать СА-проиессы для мгновенных значений величин непериодические.
1. В этом случае набор НЭ более широк - СА могут возникать, когда НЭ имеют резистивный, индуктивный и емкостный характер и являются управляемыми и неуправляемыми.
2. На вольт-амперных, вебер-амперных и кулон-волътных характеристиках НЭ. взятых отдельно от схем, падающие участки во всех случаях отсутствуют.
3. Как правило, явно выраженная обратная связь (магнитная или электрическая) при возникновении СА отсутствует.
4. Падающие участки на вольт-амперных, вебер-амперных, кулоя-вольтных характеристиках, используемых в схемах нелинейных элементов, создаются нелинейной неявно выраженной обратной связью. Она осуществляется физическими процессами, происходящими либо в самом нелинейном элементе, либо в схеме в целом.
5. СА возникают, когда изображающая точка оказывается на падающем участке вольт- амперной, вебер-амперной или кулон-вольтной характеристики НЭ или всей схемы, не прикрытом восходящими ветвями этих характеристик.
6. Если СА возникают при относительно небольших насыщениях нелинейных элементов, то высшие гармоники выражены слабо и можно говорить об огибающей процесса. Если в процессе колебаний достигаются большие насыщения и резко выражены высшие (низшие) гармоники, то процесс будет иметь хаотический характер и про огибающую процесса говорить затруднительно.
Рассмотрим упомянутые выше физические процессы, за счет проявления которых на вольт-амперных, вебер-амперных, кулон-вольтных характеристиках, используемых НЭ или в схемах в целом, возникают падающие участки.
В качестве первого назовем влияние переменной составляющей магнитной индукции на постоянную составляющую индукции при неизменной за период вынуждающей силы составляющей напряженности магнитного поля (см. § 15.17). Сходные процессы между соответствующими величинами имеют место в схемах с нелинейными конденсаторами и в схемах с нелинейными резисторами.
В качестве второго физического процесса назовем процесс возникновения постоянной составляющей в токе, протекающем через нелинейный резистивный элемент с симметричной вольт-амперной характеристикой при воздействии на него двумя гармониками напряжения, частоты которых находятся в соотношениях 1:2 (см. § 15.18), а в более общем случае как ———. где к и р — целые числа больше нуля) при отсутствии на НЭ постоянной 2 р + 1 составляющей напряжения. Сходные процессы имеют место и в схемах с нелинейными индуктивными и емкостными нелинейными элементами.
Отметим, что второй физический процесс может проявляться в виде двух разновидностей, взаимно исключающих друг друга. Так, в цепях с нелинейной индуктивностью он может проявляться, когда амплитуды первой и второй гармоник магнитной индукции в сердечнике индуктивной катушки соизмеримы по величине либо когда различаются, например. на два порядка (но тогда соизмеримыми оказываются напряженности магнитного поля первой и второй гармоник в сердечнике катушки за счет возникновения режима резонанса напряжения по второй гармонике [20. с. 297)). Кроме того, в ряде схем возможно возникновение колебаний, когда либо первый, либо второй процесс возникает при наличии в схеме неявно и явно выраженной обратной связи [20, с. 51-54].
В качестве третьего физического процесса назовем процесс в схемах с нелинейным индуктивным или емкостным элементом с симметричной соответственно вебер-амперной или кулон-вольтной характеристикой, при котором в схемах могут возникать несколько следующих друг за другом режимов резонанса напряжения и резонанса тока на одной и той же частоте источника питания схемы при изменении величины входного напряжения. В результате входная вольт-амперная характеристика схемы приобретает S-образную форму.
Приходится считаться и с тем, что первый и второй физические процессы могут сопровождать друг друга, и тогда трудно определить, действие какого из них является решающим.
Первый физический процесс, лежащий в основе действия внутренней нелинейной неявно выраженной обратной связи (ННОС) в схеме с нелинейным конденсатором был рассмотрен в §15.72.Такой же канал действия ННОС, но в схеме с управляемой нелинейной индуктивностью рассмотрен в Приложении § П9.2, а в § П9.3 — в схеме с нелинейным резистивным элементом.
Проявление второго из перечисленных физических эффектов, лежащего в основе действия второго канала ННОС, проиллюстрировано в § П9.4. Проявление третьего физического процесса, лежащего в основе третьего канала действия ННОС, проиллюстрировано в § П9.5.
В заключение отметим, что СА могут возникать и при субгармонических колебаниях в цепи (см. § 15.69).
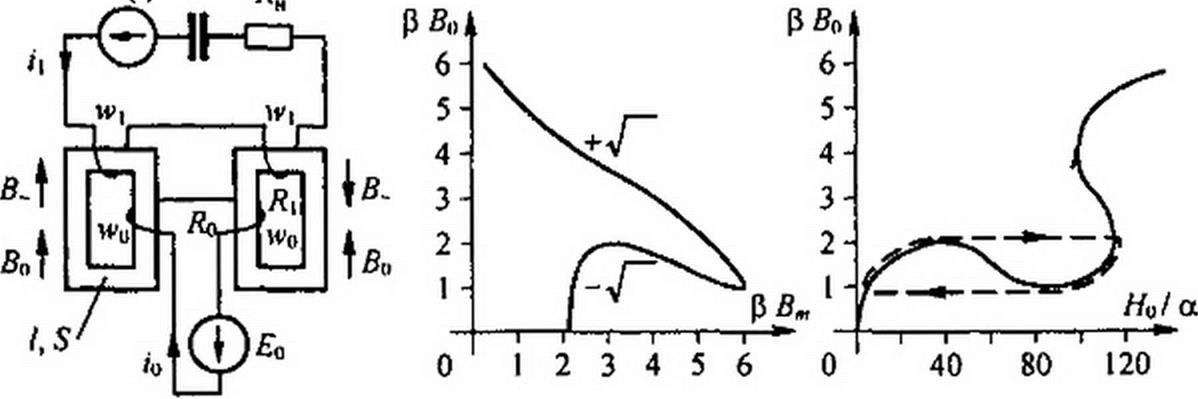
§ П9.2. Странные аттракторы в цепи с управляемой нелинейной индуктивностью. В схеме рис. П9.1, а к источнику синусоидальной ЭДС Ет sin(c>/ + v) подключены нелинейная индуктивность, конденсатор С и резистор /?р = /?н + 2 R\ (/?н — резистивная нагрузка). Цепь управления индуктивностью образована источником постоянной ЭДС EQ, катушкой с числом витков w0 и сопротивлением Rq. Направление намотки катушек на сердечник показано на рис. П9.1, а. Площадь поперечного сечения его обозначена S, а длина средней магнитной линии — 1. Положительные направления отсчета токов ц и /0, постоянной Во и переменной составляющей Вт sin со/ магнитной индукции показано на схеме стрелками.
Аппроксимируем зависимость магнитной индукции В от напряженности магнитного поля Н гиперболическим синусом Н = ashp#, высшие гармоники не учитываем. Запишем уравнение по закону полного тока для левого сердечника:
6 wi + 'о ‘♦'о = а /Р( До + sin <о /) (П9.1)
и для правого
й W| -i0 w0 =а /shP(-B0 + Вт sin со/). (П9.2)
Уравнение (П9.1) сложим с уравнением (П9.2), получим формулу для первой гармоники тока
= —chptf0 J.QpB^sinco/. (П9.3)
»■]
Из уравнения (П9.1) вычтем уравнение (П9.2). Получим
4> н>0 = <х /shp/?0 J0(J р Вт]. (П9.4)
Из (П9.4) следует, что
/0= —shp50 JO(; PBW). (П9.5)
И'О
Составим уравнение по второму закону Кирхгофа для цепи переменного тока:
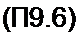 2 W] S —Вт sin со/ + /| Яр + — Jq dl = Е„, sin(co/ + v).
2 W] S —Вт sin со/ + /| Яр + — Jq dl = Е„, sin(co/ + v).
d t
 |
|
 |
Рис. П9.1
В уравнение (П9.6) подставим ток /, из (П9.3) и выделим в полученном выражении синусные и косинусные компоненты, возведем их в квадрат, сложим для устранения угла v, и полученное уравнение разрешим относительно ch 0 #0:
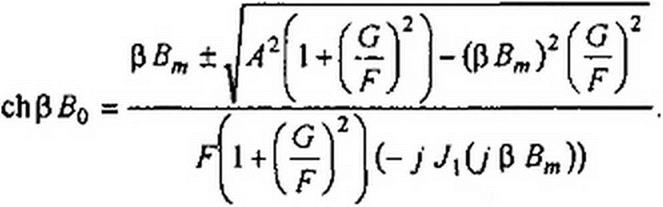 | |||
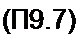 | |||
Здесь
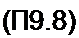 2a0Z с_ 2aZpflp (j £„
2a0Z с_ 2aZpflp (j £„
м'|2 S W2 С со w2 $ 2 w и»] 5
При параметрах А - 2.2, F = 0,054, Gl F = 0,3675 на рис. П9.1, б по формуле (П9.7) построим зависимость 0 BQ от Р В„. Нижняя ветвь кривой на этом рисунке соответству* ет знаку минус перед корнем в формуле (П9.7), верхняя — знаку плюс. Используя зависимость 0£о от Р Вт рис. П9.1, б по формуле W0/a = sh0Bo J0(y 0 5т) на рис. П9.1, в, строим зависимость Р Во = /(Я0/а). Замечаем, что на этой зависимости в диапазоне значений Но / a - 30-76 имеется падающий участок, не прикрытый восходящей ветвью кривой (при указанных значениях параметров восходящая ветвь только начинает образовываться’1). Опишем падающий участок уравнением прямой
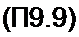 0£o="-*—.
0£o="-*—.
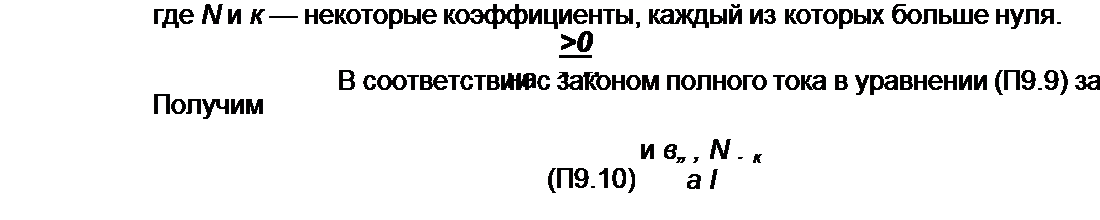 |
Составим уравнение для цепи управления:
(П9.11)
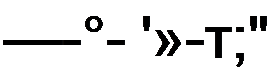 и исследуем, будет ли устойчиво положение рабочей точки на падающем участке характеристики р50= на рис. П9.1, а.
и исследуем, будет ли устойчиво положение рабочей точки на падающем участке характеристики р50= на рис. П9.1, а.
В установившемся неколебательяом режиме работы
(П9.12)
’’Деформация зависимостей 0So=/(0 5m) и = sh05o JQ(J 0 Bm) = f($ Bm) при изменении параметра А от 0,5 до 5, параметра F в диапазоне от 0.054 до 0,151 и величины С / F в интервале от 0,1 до 0,3675 с целью экономии места здесь не приведена, с ней можно ознакомиться в § 2,2-2,7 [25].
Если катушки iv, нелинейной индуктивности в схеме рис. П9.1, а будут соединены не последовательно, а параллельно, то результирующее резистивное сопротивление в цепи у^
переменного тока будет равно , где /?, —это резистивное сопротивление одной катушки а Rn — сопротивление нагрузки. В этом случае параметры A, F, G в формуле (П9.7) будут равны
. 0£„, с 2а0/ _ 2а/0(Ян+0,5
А ~----------- 7Г’ ~' ° =---------------------------------------- ?-----------
о W1 S W|2 S с/ С со wf S
Пусть ток io получил приращение Д>о флюктуационного происхождения и стал равен /0+Д<0. Приращению Д/о по уравнению (П9.12) соответствует приращение △р50 = -к А,° W° . По уравнению (П9.11) составим уравнение для приращений:
а I
_2^Sk = 0
а/p dt
Алгебраизируем его и получим характеристическое уравнение (П9.14)
£ДоР + /?о=0. (П9.14)
2 к Wq S
Здесь £л0 =-------------- 2— представляет собой отрицательную дифференциальную индук-
м а I р
тивность для малых приращений Д/о и Д0Яо. Корень уравнения (П9.14) положителен; следовательно, положение рабочей точки на падающем участке характеристики рис. П9.1, в неустойчиво, и в цепи начнется автомодуляция или хаос (см. осциллограмму напряжения на нелинейной индуктивности на рис. П9.1,г). Огибающая колебаний имеет релаксационный характер. Нелинейная неявно выраженная обратная связь осуществляется в схеме через реагенты Во и Вп, в соответствии с уравнениями (П9.3), (П9.5), (П9.7).
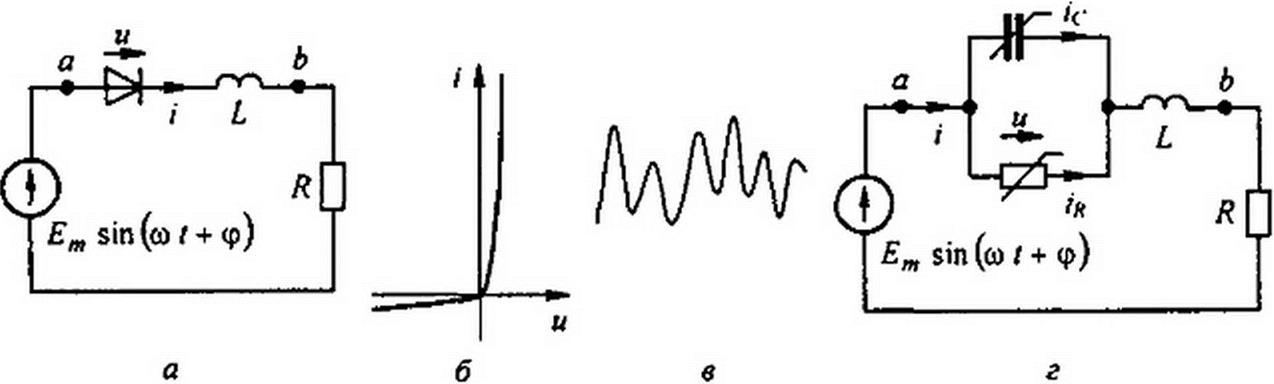
§ П9.3. Хаос в диодной схеме выпрямления. На рис. П9.2, а изображена простейшая диодная схема выпрямления. В ней на частоте порядка I МГц при работе диода на начальном участке его ВАХ (утолщенная линия на рис. П9.2, б) и при определенных параметрах схемы (значениях L, R и амплитуде синусоидальной ЭДС Ет sin(w t + <p)) возникает хаос (рис. П9.2, в). Хаос возникает потому, что первая гармоника напряжения на диоде sin <о / так влияет на постоянную составляющую напряжения на диоде UQ, что дифференциальное сопротивление диода /?до, посчитанное по приращению постоянной составляющей напряжения на диоде Д»о и соответствующему приращению постоянной составляющей тока через диод Дг0(т. е. /?до = Ди0/Д/0), при определенных значениях параметров оказывается отрицательным.
При анализе процессов в схеме используем схему замещения (рис. П9.2, г). В ней диод представлен параллельным соединением резистивной ветви, ВАХ которой описана фор-
 |
|
 |
|
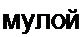 |
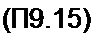 iR =5(сАи-1)
iR =5(сАи-1)
и емкостной ветви, дифференциальная емкость которой описана формулой Сл = А еаи.
В исследовавшейся схеме высокочастотный диол имел следующие параметры: 5 = ЗЮ~8А; д = 17,4В"1; А = 3,88- 1О"10 А с/В; а = 0,528 В“'.
Полагаем, что напряжение на диоде и « Uo + Um sin © t. Высшие гармоники в первом приближении не учитываем.
Разложим функции е°" и еА" в ряды по функциям Бесселя от мнимого аргумента и определим ток i:
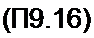 i = iR +
i = iR +
i(- - A eaU(> - Atau <aUm J0(j a Um)cosco t.
Подставим ток i и напряжение и в дифференциальное уравнение:
и+ Ri+ L~ = Ет sin(co/ + (p). (П9.17)
dl
Выделим из (П9.17) уравнение (П9.18) для постоянных составляющих
Uq^-R В^иЧ^Ьит}-\=0. (П9.18)
Уравнение для синусных и косинусных составляющих первой гармоники:
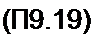 + R 1п,п -<aL/mC- = Eni coscp;
+ R 1п,п -<aL/mC- = Eni coscp;
^LImK + R /тС = Ет sincp.
Здесь — амплитуда резистивной, а /от(— амплитуда емкостной составляющей тока через диод:
 | |||
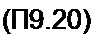 | |||
Возведем уравнение (П9.19) в квадрат и сложим. Получим уравнение, которое дает связь Uq, U„, и Е„:
«Л, + Л U-al /м-)2 +(« i 1яК + Я/,,)2 = £2. (П9.21)
Зависимость токов lmR и 1„с <>т амплитуды напряжения Um на диоде изображена на рис. П9.2, д. По уравнению (П9.18) при R = 200 Ом на рис. П9.2, е построена зависимость U„ от Uo при работе на начальном участке ВАХ диода. Из рисунка видно, что кривая сначала круто поднимается вверх, затем рост Um становится незначительным . Используя рис. П9.2, е, построим график зависимости отношения между прира
щениями в функции от UQ (на рис. П9.2, ж).
После этого исследуем устойчивость периодического режима работы схемы, для чего положим, что Uq получило малое приращение Дц0 и стало равным Uo + Дн0 и что синусоидальное напряжение на диоде при этом стало равным (Uт +6U„)sin(<иt + Ду), где Д1/„ « Um и А\р <к л.
Слагаемые Ri и L— уравнения (П9.17) тоже получили приращения. Приращения di
всех слагаемых (П9.17) выразим через приращения Ди0. Получим дифференциальное уравнение относительно приращений’’.
’’Подробнее о приращениях см.: Бессонов JI.А. Аномальные режимы работы диодной схемы выпрямления // Радиоэлектронные устройства и системы обработки информации. М.: МИРЭА, 1996.
После алгебраизации его характеристическое уравнение относительно приращений принимает вид:
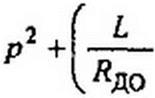 |
|
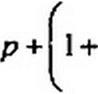 | |||
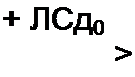 | |||
|
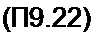 |
В нем дифференциальное сопротивление диода для малых приращений постоянных составляющих напряжения и тока
R , 1
до Д/'о ь В ед и° F ’
где
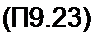 Г = JQ(J b Um)-\~{~j Jjjb
Г = JQ(J b Um)-\~{~j Jjjb
дс/0
а дифференциальная емкость диода для малых приращений
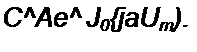 | |||
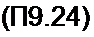 | |||
При работе на начальном участке ВАХ диода отношение приращений Ы1т1&и0 достаточно велико (см. рис. П9.2, ж) для того, чтобы функции F и /?до оказались отрицательными. Хаос возникает при условии |£/Ядо|> RC^q. Движения в системе при воз-
в , R
никновении хаоса могут быть различными в зависимости от значения слагаемого 1 +-------------------------------------------
Ядо
в уравнении (П9.22). При прочих равных условиях хаос начнется при некотором минимальном ЕтХ и прекратится при некотором максимальном Ет2. Величина Е„} обусловлена тем, что ток, протекающий по резистивной ветви схемы замещения диода (см. рис. П9.2, г), сначала очень мал (см. рис. П9.2, д) и влияние отрицательного /?до в токе i еще не может проявиться. При некотором значении Е„2 хаос прекратится ,так как отношение MJm/bU0 при этой ЭДС становится недостаточным для того, чтобы /?до стало меньше нуля.
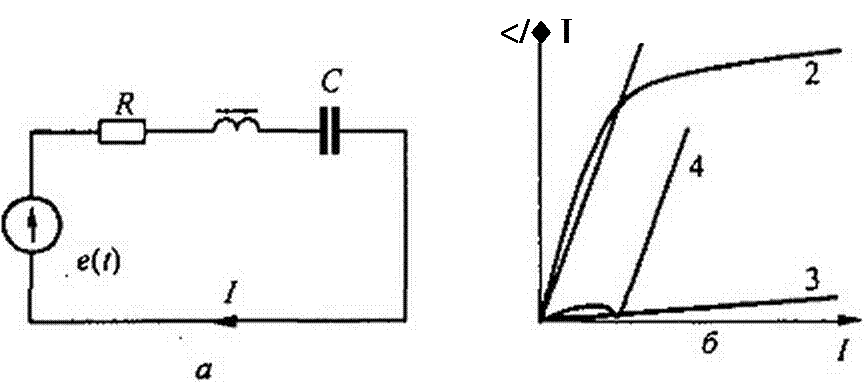
§ П9.4. Хаос, обусловленный нелинейным взаимодействием нулевой, первой и второй гармоник. Схема, приведенная на рис. П9.3, а, образована линейным резистором R, линейным конденсатором С. нелинейной индуктивностью и источником синусоидальной ЭДС Е„ sin(w t + v). В этой схеме взаимодействие первой и второй гармоник магнитной индукции в сердечнике нелинейной индуктивности вызывает появление постоянной составляющей индукции при отсутствии постоянной составляющей в напряженности магнитного поля. Режим работы цепи при этом может быть либо устойчивым, либо неустойчивым — тогда в цепи возникает хаос. При возникновении хаоса в токе и в индукции появятся медленно изменяющиеся постоянные составляющие.
На рис. П9.3, б показаны вольт-амперные характеристики элементов схемы по первой гармонике: конденсатора (прямая /), нелинейной индуктивности (кривая 2), резистора (прямая 3) и всей схемы (кривая 4).
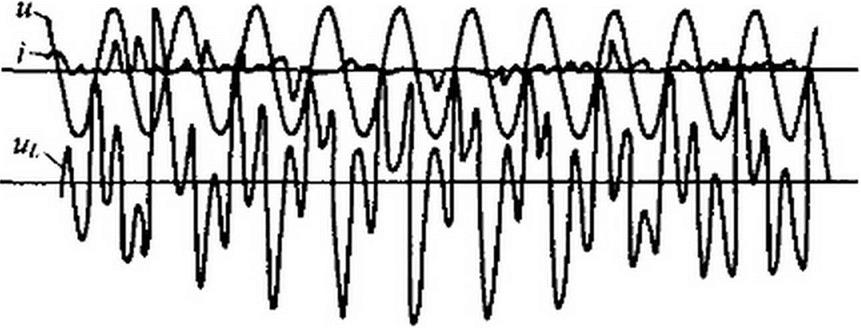
Осцилограмма хаоса в схеме рис. П9.3, а представлена на рис. П9.3, в, где и — входное напряжение, i — ток, и/ — напряжение на нелинейной индуктивности.
При анализе процессов в схеме положим, что нелинейная индуктивность имеет w витков при длине средней магнитной линии сердечника / и его площади поперечного сечения S. Кривая намагничивания ферромагнитного материала сердечника описана формулой
tf=ash0S, (П9.25)
где Н — напряжение магнитного поля, а В — магнитная индукция.
Полагаем, что
В = BQ + 5)m sin о l + В2т sin(2 <о/ + q>). (П9.26)
 | ||
 | ||
e
Рис. П9.3
Подставим индукцию В по формуле (П9.25) в формулу (П9.24) и из полученного выражения определим постоянную Но, а также синусные и косинусные составляющие первой и второй гармоник напряженности магнитного поля, а по ним, используя закон полного тока, синусные и косинусные компоненты тока первой и второй гармоник:
= sh р Во Jq(j р ) J0(j Р U2a) + 2 ch 0 BQ J2(j р Л1л,) (-J J,(j Р В2т)) sin Ф. (П9.27) а
В установившемся нехаотическом режиме работы Но-О (конденсатор постоянный ток не пропускает). Из формулы (П9.27) следует .что
2 А
thP Во = —Sincp;
Л = Л(-7 Р j (П9.28)
В = Р &\т ) Р ^2«)-
Формула (П9.28) позволяет определить РЯО через Р^1т. Р В2т и угол ф. В дальнейшем для более компактной записи уравнений обозначим
Р В\т = х, Р В2т = у, р BQ = г.
Ток i = + i2. Здесь i} — первая, а /2 — вторая гармоника тока i:
2 а / , .
/] --------- (n, sin со t + т} cosco/);
2а/, . _ . .
i2 -- («2 Sin 2 co I + т2 cos 2 со /);
«j = CchZ -shZ- Psincp, = DshZ со$ф,
C = Jo{jy){-jJ\(j x)\ D-i^j (j y))((- j J,(j x))-(j Jj(j x)));
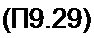
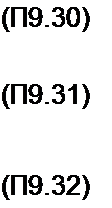
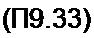 = chZ • Л coscp-shZ Csin2 ф, m2 = chZ ■ F sin<p + shZ (G со$2 ф + Л/),
= chZ • Л coscp-shZ Csin2 ф, m2 = chZ ■ F sin<p + shZ (G со$2 ф + Л/),
= Jq (j x) (~jJ}(J y)\ G = J2(j x) J2{j y\ M =J0(j y) J2(j x)
Затем для схемы на рис. П9.3, а составим уравнение по второму закону Кирхгофа:
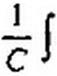
|
|
(П9.34)
где v — потокосцепление нелинейной индуктивности, равное w 5 В. Продифференцируем уравнение (П9.34) по времени , подставим в полученное выражение индукцию В по формуле (П9.26) и токи и i2 по формулам (П9.30) и (П9.31). Выделим из полученного уравнения синусные и косинусные компоненты первой и второй гармоник. Затем все слагаемые уравнений для первой гармоники поделим на коэффициент при х = р Bim, а все слагаемые уравнения для второй гармоники на коэффициент при у - Р В2т.
Получим два уравнения (П9.35) для синусных и косинусных составляющих первой гармоники:
-х+Г| 77?t +х(ч = -esinv, г} + хС) т} = ecosv, (П9.35)
где
п2а/р . 1 2а/р л с Р .
Л =Л--------- хп ~ —--------------- т—, е = Ет----------------
а ж2 5 1оСои>2$ сои-5
а также два уравнения (П9.36) для синусных и косинусных составляющих второй гармоники
х(-2 п2 - г2 т2 - у sin ф, х^2 /я2 + г2 п1 ~ ~У со$Ф»
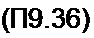 ,ас п а/р . 1 а/р
,ас п а/р . 1 а/р
r2- R----------- —, хГ2 --------------------- г—.
со w2 S 2 со С о w2 5
Введение обозначений г,, хС1> г2, хС2 привело к тому, что все величины в (П9.35) и (П9.36) стали иметь нулевую размерность. Возведем в квадрат левые и правые части уравнений (П9.35) и сложим их.
Получим (-х-Г] +Х(ч Л))2 +(Г] И| +хС| /Л])2 = е2 или
х2 - х (хп И| - г, лц) + (г2 + х2)) (и2 + т2) = е2. (Г19.37)
Подставим в (П9.37) выражения для z?| и /Ир После небольших преобразований получим
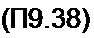 х2 - 2х(С х*! ch с- D shz (х(-, sin ф cosq) +
х2 - 2х(С х*! ch с- D shz (х(-, sin ф cosq) +
+ (Г)2 +х*,)(С2 ch2z + £>2 sh2 z-D C sh2 z) = e2.
Аналогичные выкладки по отношению к уравнению (П9.36) дают
(r22 + x2Ci) ( F ch2 z + sh2 z (G2 +A/2 + 2G Л/cosV) + sh2z F(A/-G)sincp = >-2. (П9.39)
Выразим ch2r, sh2z. sh2z, chz, shz через thz:
u2 । 2thr
ch z = -——sh2z =------------------- —,
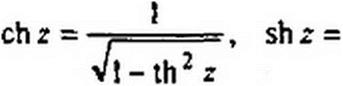 |
|
 1-thz l-th2z
1-thz l-th2z
и подставим соответствующие функции в уравнения (П9.38) и (П9.39)
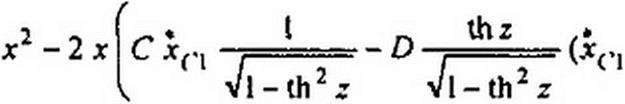 |
|
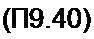 | |||||
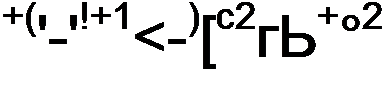 | |||||
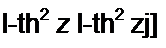 | |||||
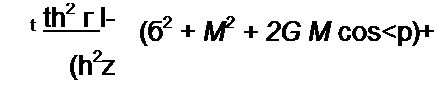 | |||||
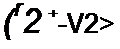 | |||||
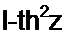 | |||||
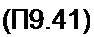
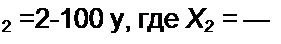
2thz . _ . ] 2
------ — (M - G) sin <p I = y. 1- th2z------- J
Рассмотрим, как можно выявить возникновение устойчивого периодического процесса, для которого характерно наличие в магнитном потоке нелинейной индуктивной постоянной составляющей, первой и второй гармоник при отсутствии постоянной составляющей в напряженности магнитного поля.
Будем последовательно задаваться значениями х в диапазоне примерно от 1,5 до 4. При каждом выбранном значении х величине у будем последовательно придавать значения 0,2,0,4,... (у < х). Подставляя эти значения хиу в уравнение (П9.41), путем прогонки на ЭВМ выясняем для каждого сочетания х ну, при каком значении угла ср будет возможно удовлетворить уравнению (П9.41). После выявления совокупности возможных сочетаний значений х, у, <р, при которых уравнение (П9.41) удовлетворяется, по уравнению (П9.40) для каждого сочетания х и у определяем величину е, а по ней — амплитуду ЭДС на входе цепи.
Хаос в цепи рис. П9.3,а возникает, когда величина сопротивления конденсатора по
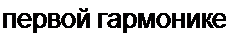 меньше величины сопротивления нелинейной индуктивности
меньше величины сопротивления нелинейной индуктивности
по первой гармонике при малом токе через нее, при небольшом сопротивлении R (см. рис. П9.3, б) и при значении х, находящемся в диапазоне, примерно, от 1,6 до 4,
Для определения диапазона значений параметров схемы С, со, R, а, 0 и величин х, при которых в цепи возникает хаос, надлежит обратиться к § 18.7. В нем рассмотрена методика исследования устойчивости периодических режимов работы нелинейной цепи рис. 18.7, а (такой же, что и цепь рис. П9.3, а), когда вольт-амперная характеристика цепи была Л'-образна. В соответствии с этой методикой дифференциальное уравнение нелинейной цепи по отношению к малому возмущению потокосцепления нелинейной индуктивности было сведено к линейному дифференциальному уравнению второго порядка с изменяющимися во времени параметрами (к уравнению Матье):
—у- + (а +16 b cos 2 т) т| = 0. dt
Затем использовался график областей устойчивых и неустойчивых решений уравнения Матье, представленный на рис. 18.7, в.
Устойчивость определялась по значениям коэффициентов а и Ь, зависящих от всех параметров схемы рис. 18.7,0 (а следовательно, и рис. П9.3, а), дана выражениями (П9.41) и (П9.36) § 18.7. Эта методика полностью применима и к определению условий возникновения хаоса рассматриваемого типа.
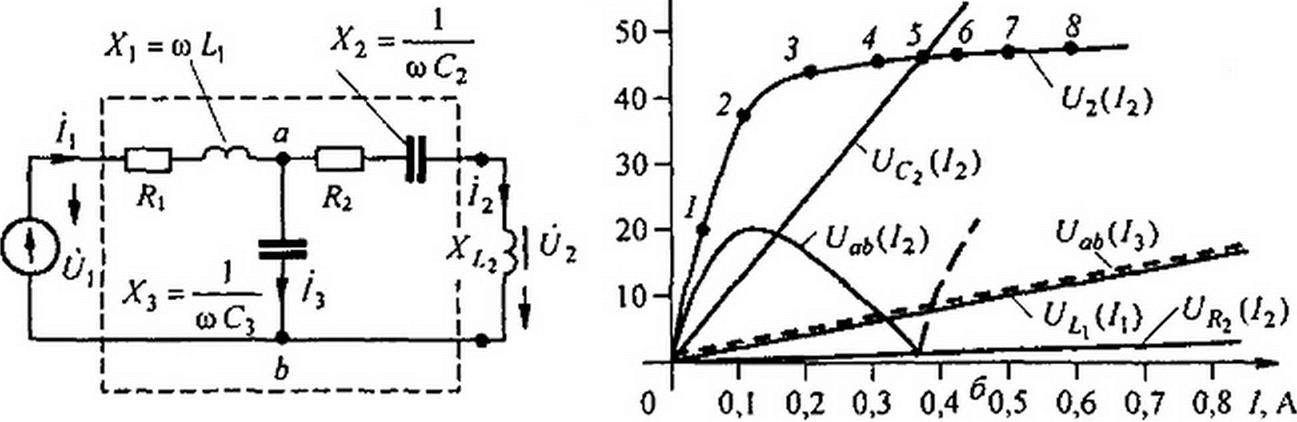
§ П9.5. Автомодуляция, обусловленная резонансными явлениями в электрической цепи при неизменной частоте источника питания. На рис. П9.4, а изображен линейный четырехполюсник, на входе которого— источник синусоидальной ЭДС, на выходе — нелинейный индуктивный элемент, вольт-амперная характеристика которого L/2 = /(/2) представлена на рис. П9.4. б. Четырехполюсник представлен Г-схемой. Сопротивление первой ветви его Zt = RK + j Хъ где Х} = ш L., сопротивление второй ветви —
третьей ветви — Z3 - -j Х3, Xt - Х3 = 20 Ом, /?t = R2 = 2 Ом. Модуль емкостного сопротивления Х2 = 100 Ом. Сопротивлению Х2 на рис. П9.4, а соответствует прямая на рис. П9.4, б, а сопротивлениям Я, и R2— прямая R2. Подсчитаем параметры А, В, С. D четырехполюсника (см. формулы 4.35) на частоте источника питания:
Л = 1 + -^ = 0,1 у; 5 = Z,+Z2+^2- = 12 + 20,2 J;
z i Z3
С = —= 0,05; Ом; D = 1+ ^ = 6 + 0,1; Ом.
Z3 Z3
t/,B
a 6
в г д
Рис. П9.4
Цифрами 1-8 на ВАХ нелинейного индуктивного элемента U2 - JV2) на рис. П9.4, б обозначены точки, которым соответствуют одноименные точки на S-образной входной ВАХ всей схемы изображенной на рис. П9.4, в. Подсчеты соответст
вующих друг другу значений Ц и проводились по формулам Ц = А 02 + В /2 и /1 = С U2 + D 12. Результаты подсчетов Ц и /, и соответствующие им значения 02 и /, а также численные значения модуля сопротивления нелинейного индуктивного элемента
jXt = по первой гармонике записаны в табл. П9.1.
1 2
Линейный четырехполюсник преобразовал монотонную ВАХ нелинейной индуктивности рис. П9.4, б в S-образную ВАХ всей схемы рис. П9.4, в. Поясним, почему зависимость
Таблица П9.1
| т • | Номера точек на кривой U2 =JUi) и на кривой (Л -Д/0 | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| </2,в /2,А Л7, Ом ц.в А | 20/ 0,04 500 1,72е'“’- 0,76 е'179 | 37/ 0,1 370 3,2 eyUI* 1.25 е'|7х | 44/ 0.2 220 4,5 е;|26* 1,6 е'17' | 45/ 0,3 150 6,12 е'94’ 0,45 еА’1 | 46/ 0,37 124 7.47 е'”’ 0,09 е'156 | 46,5/ 0,4 116 8,1 е'90’ 0.08 е'14’ | 47,3/ 0,47 100 10,1 с'1’’ 0,64 еА’ | 48; 0,6 80 12,3 е™ 1,21 e'w |
4/( = /(/]) приобрела 5-образную форму Дело в том, что в интервале точек 0—1—2 на ВАХ 4/2 = /(^г) полное сопротивление второй ветви, равное Z2 + j X L , остается по модулю достаточно большим (400 + 270 Ом) и не может помешать возникновению режима резонанса напряжений как бы последовательно соединенных первой и третьей ветвей схемы (суммарное сопротивление ветвей / и 3 примерно равно 4 Ома). В точке 3 на рис. П9.4, б сопротивление второй ветви равно 2 + /120 Ом. В режиме соответствующем точке 4 вторая и третья ветви находятся в состоянии, близком к режиму резонанса токов, поэтому входной ток /1 уменьшился. В режиме, соответствующем точке 5, во второй ветви возникает резонанс напряжений, сопротивление ее снижается примерно до 2 Ом, а модуль входного сопротивления схемы примерно до 20 Ом. Точка 6 на ВАХ U2 = f(Jz) соответствует сопротивлению второй ветви около (2 + 20 у) Ом, а входное сопротивление всей схемы оказывается примерно равным (2 + 10у) Ом. Таким образом, при подъеме входного напряжения с нуля в схеме последовательно возникают три следующих друг за другом различных резонансных режима на частоте источника ЭДС.
Одновременно с изменением величины тока /2 возникает Лг-образная вольт-амперная характеристика второй ветви и 5-образная вольт-амперная характеристика всей
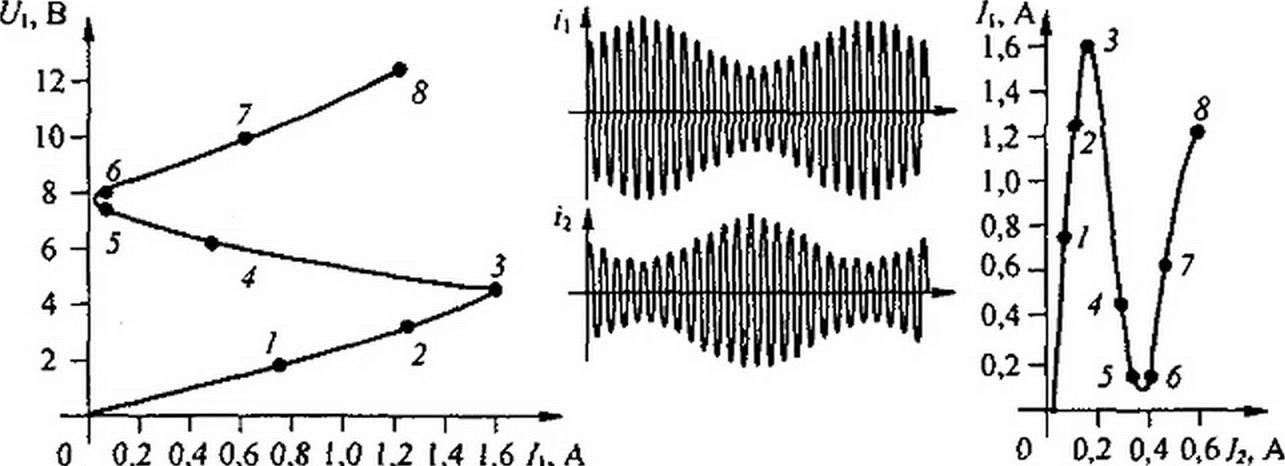
схемы Z7i(/t). Падающий участок Л'-характеристики соответствует падающему участку 5-характеристики. Так как работа на падающем участке У-характерисгики отдельно взятой второй ветви неустойчива, (см. § 18.7), то неустойчивой оказывается работа и всей схемы рис. П9.4,п на падающем участке характеристики Ц(/(). Если величина входного напряжения в примере окажется в интервале (4,5 +7,2) В, то в схеме возникнет автомодуляция (рис. П9.4, г). При АМ рабочая точка перемешается по падающему участку характеристики /|(/2), причем увеличение тока по характеристике сопровождается уменьшением тока /2 (см. табл. 1 и рис. П9.4,д; цифры 1-8 на нем соответствуют цифрам 1-8 на рис. П9.4, б и в), поэтому между огибающими амплитуд токов н <2 на рис. П9.4, г имеется сдвиг фаз, зависящий от параметров цепи рис. П9.4, а и величины Uv При АМ изменяются не только значения амплитуд, но и мгновенные значения фаз токов q и i2.
Далее рассмотрим, почему в симметричной выпрямительной схеме может возникать «странный» режим работы.
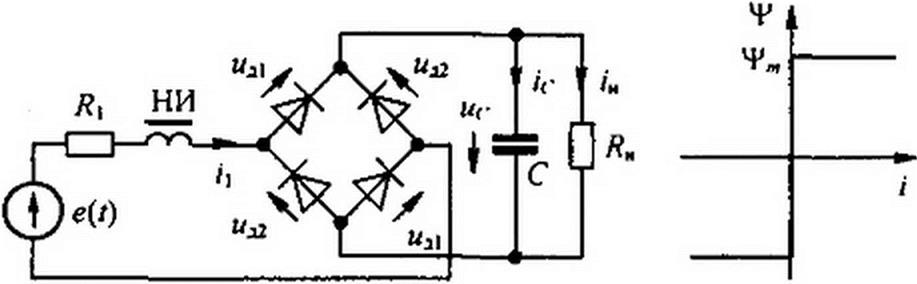
§ П9.6. Аномальный режим работы симметричной мостовой выпрямительной схемы. Схема изображена на рис. П9.5, а. К синусной или в виде меандра ЭДС e(t) присоединены резистор Л(, управляемая нелинейная индуктивность НИ, выпрямительный мост, на выходе которого нагрузка Лн и шунтирующий ее конденсатор С.
Вебер-амлерная характеристика нелинейной индуктивности симметрична и близка к идеально прямоугольной (рис. П9.5, б). Вольт-амперные характеристики диодов тоже близки к идеально прямоугольным (рис. П9.5. в).
 |
а б
Рис. П9.5
Аномальный режим рассматриваем в данном параграфе при разомкнутой цепи управления НИ (так, что НИ работает в режиме неуправляемой НИ).
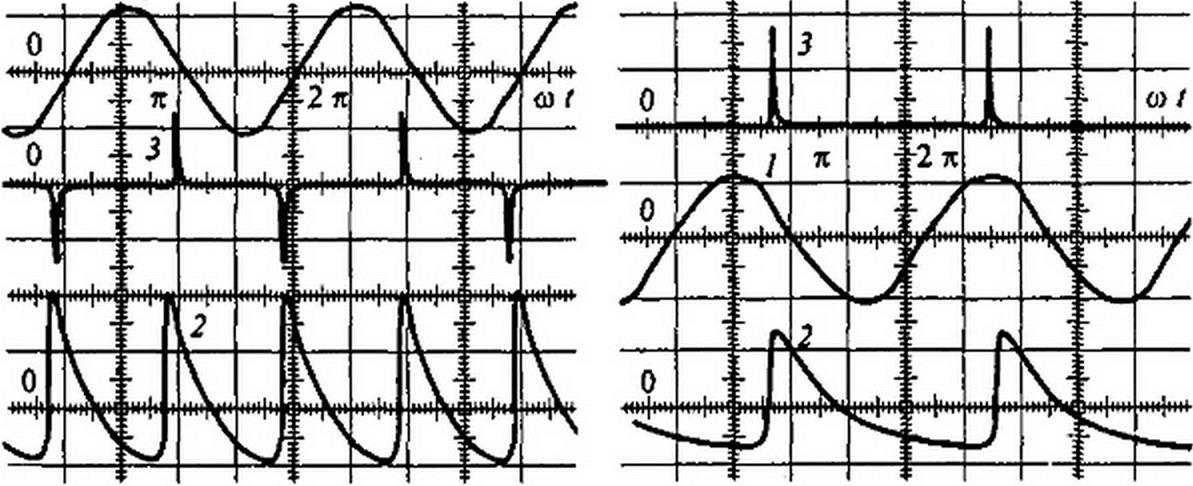
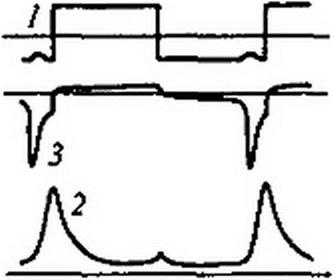
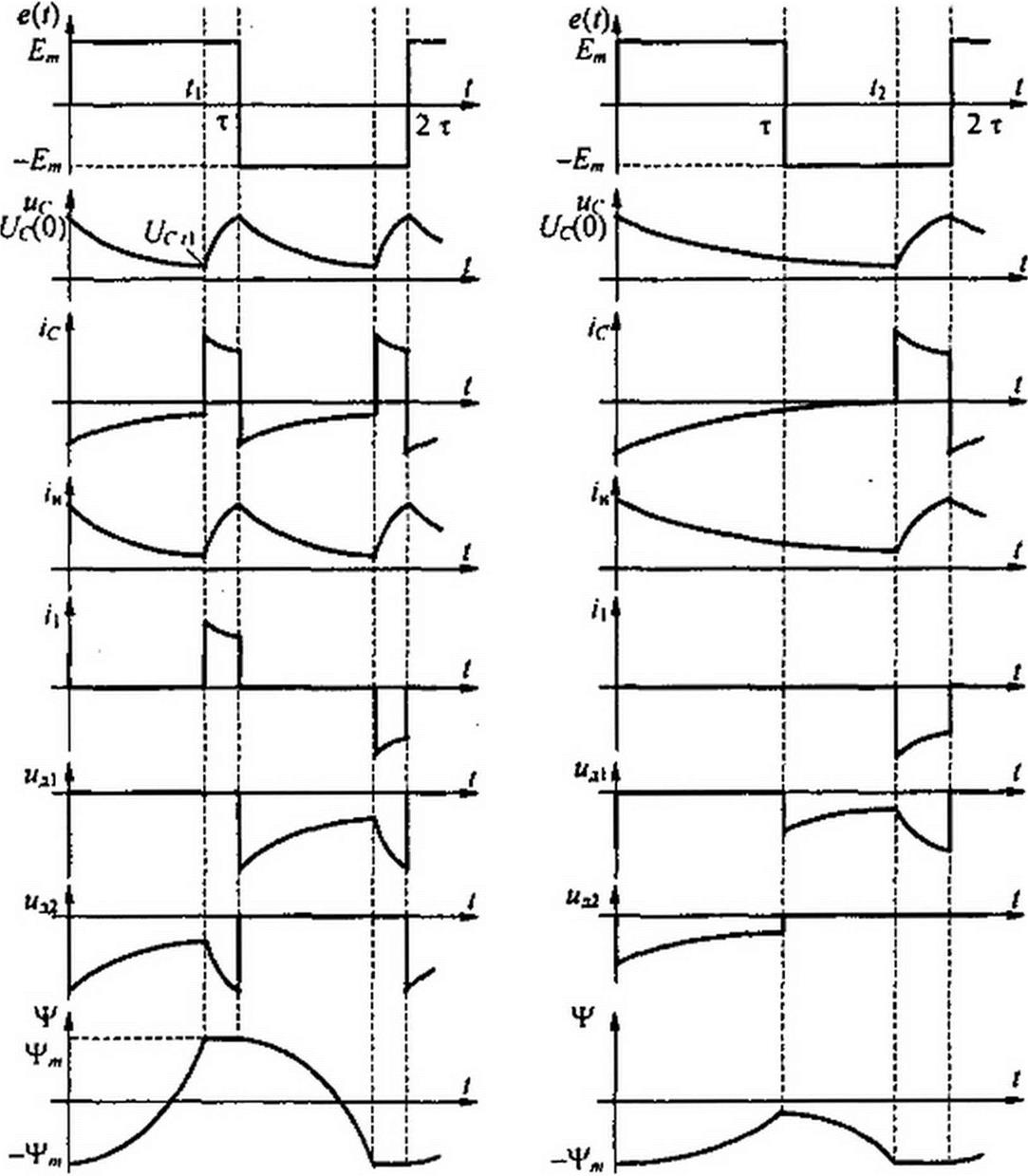
Осциллограмма нормального режима при синусоидальной ЭДС e(t) дана на рис. П9.6, а, а аномального — на рис. П9.6, б. Цифрой / на них обозначена ЭДС е(/), цифрой 2 — напряжение на выходе выпрямительного моста, цифрой 3 — ток /, через НИ и резистор Я].
 |
|
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
|
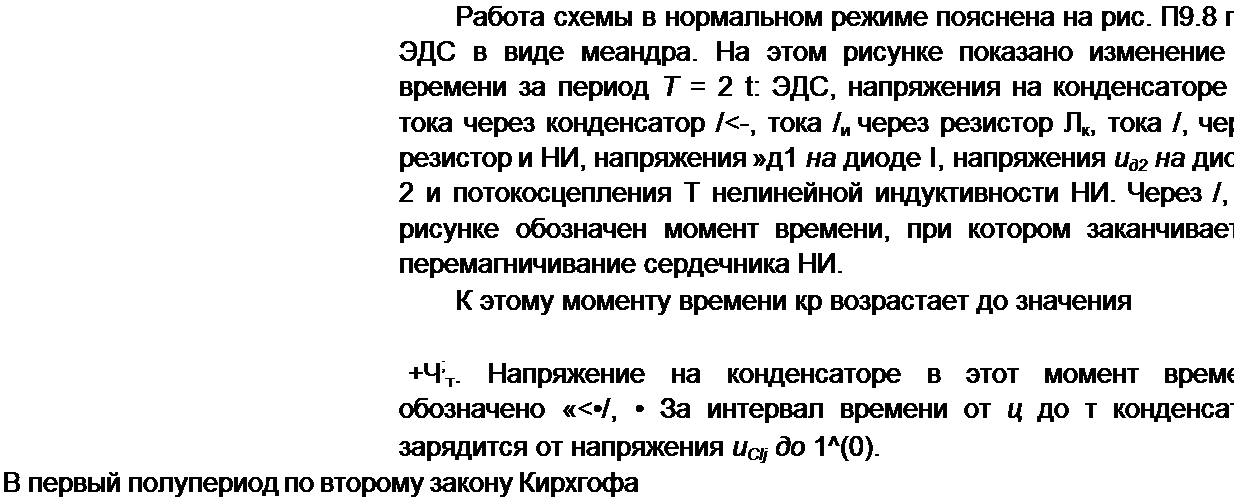 | |||||||
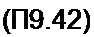 | |||||||
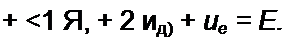 | |||||||
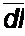 | |||||||
В интервале 0 + /| ток = 0, ая1 = 0, поэтому
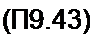 ^~- = £-ис(0)е’//Л"г
^~- = £-ис(0)е’//Л"г
Интегрируя это уравнение по времени и учитывая, что Т = -4% при / = 0, получим закон изменения потокосцепления на интервале 0 + /,:
4'^£/ + RHCwr(0)(e"'/^r-l)-4'Jn. (П9.44)
При I = потокосцепление Т = поэтому из (3) следует
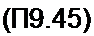 2 = Е г, + Ян С ис (0) (е'/1/Л*r -1).
2 = Е г, + Ян С ис (0) (е'/1/Л*r -1).
Поделив обе части (П9.45) на Е т, получим
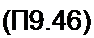 Uk М2) С)
Uk М2) С)
Е т т Е т
 |
|
В интервале времени от до т напряжение на диоде wai = О, Ч7 =Ч?Я)= const, а ток
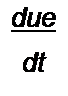 | |||||
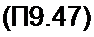 | |||||
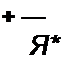 | |||||
Обозначим а = 1 + /Л„ и запишем уравнение (П9.42) для этого интервала времени
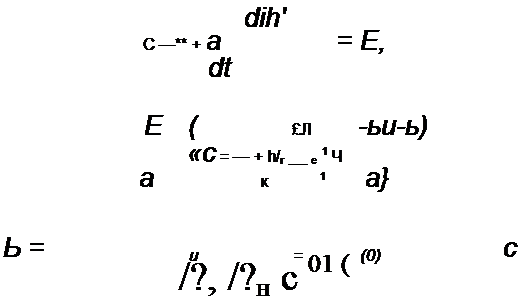 | ||||||
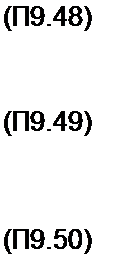 | ||||||
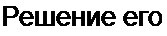 | ||||||
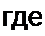 | ||||||
При t = т напряжение на конденсаторе «г(т) = «<-(0). Из (П9.49) следует:
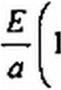 |
| ||||
| ||||
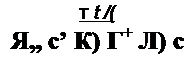 | |||
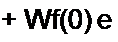 | |||
 | |||||||
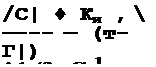 | |||||||
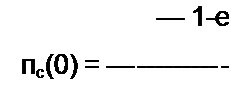 | |||||||
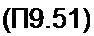 | |||||||
1_е V W
Среднее за полпериода значение выпрямленного напряжения на емкости мГср определим, проинтегрировав по времени обе части уравнения (П9.42) за полпериода т:
(П9.52)
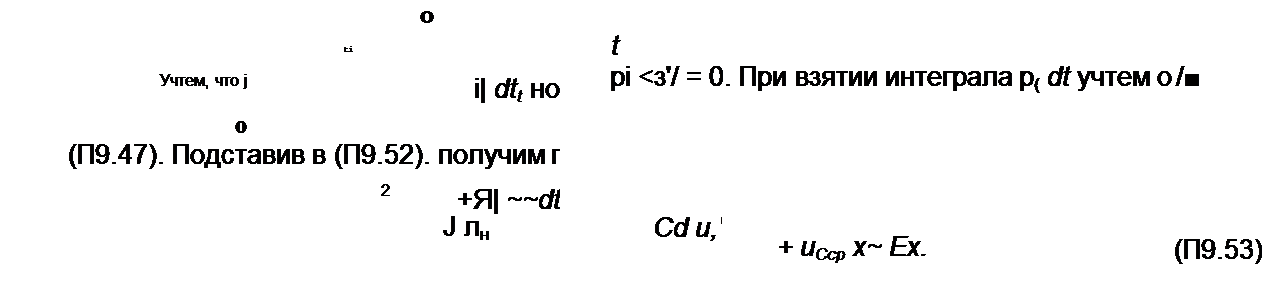 |
После интегрирования в (П9.53) запишем выражение для М(-Ср;
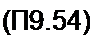 _ 2>Р„ + Л, С МО) С ‘ )
_ 2>Р„ + Л, С МО) С ‘ )
"Сер ~ 5------------------------------ ----------------------------------------- ----------------------------------------- -----------------------------------------
В силу симметрии процессов а первом и втором полупериодах формула (П9.54) спра- всдлива и для второго полупериода.
Пояснения к возникновению асимметричного режима работы сопроводим рис. П9.9. Асимметричный режим возникает, когда конденсатор в первом полупсриодс будет разряжаться через резистор /?и достаточно медленно, так что интеграл от напряжения на не- }dV . , линейной индуктивности за полупериод 0-^т (вольт-секундная площадь ]——-dt) о
окажется меньше 2Ут, при этом потокосцепление нс достигнет величины +%„ и станет равным к <¥т {к < 1).
В этом случае конденсатор будет продолжать разряжаться на /?н и во втором полупериоде до времени /2, при котором потокосцепление уменьшится на величину к (этот процесс происходит при меньшем wc-(0, чем в первом полупериоде), потокосцепление
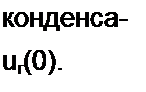 окажется равным производная —— станет равной нулю и при /2 <2т t 4 \
окажется равным производная —— станет равной нулю и при /2 <2т t 4 \
тор в интервале времени /2т2х начнет заряжаться от напряжения uc(i2) д0
Процесс зарядки конденсатора вновь описывается уравнением (П9.48):
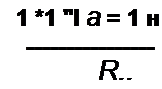 | |||||||||||
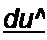 | 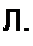 | ||||||||||
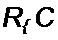 | |||||||||||
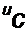 | |||||||||||
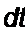 | |||||||||||
Решение этого уравнения
е /«.Янг*
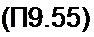 При t = 2 т и(' становится равным
При t = 2 т и(' становится равным
«с(0) = ~
[_с Чгас'/?!<’
При неизменных параметрах Ян, С. Я|, увеличение Е или появление тока в цепи управления НИ, а также при изменении какого-либо одного параметра (Ян, С, /Jt, Tw)
при неизменных £ и т, появляются пики тока неравной амплитуды и в первом, и во втором полулериоде; при дальнейшем увеличении любого параметра пики тока /( в обоих полупериодах выравниваются и в цепи управления устанавливается симметричный режим работы.
§ П9.7. Математический критерий возникновения хаоса. Хаос может возникать во многих областях физики, механики, химии, биологии, медицины. Это вызвало потребность в разработке общего чисто математического критерия определения условий возникновения хаоса в системах самой различной природы, не выясняя причины, почему он возникает. Обобщенный математический подход к хаосу используется в синергетике (37], в теории катастроф [35], в теории хаоса [36]. В синергетике рассматривают роль коллективных эффектов в процессе самоорганизации процессов природы. В основу ее положены три основных положения :
1) принцип подчинения (учет основных эффектов за счет членов уравнений, содержащих малые параметры);
2) принцип самоорганизации (последовательности фазовых переходов в системе при изменении управляющего параметра);
3) предположение о том, что при добавлении к линейной недиссипативной системе небольших нелинейностей регулярные движения в ней будут продолжать существовать.
В основу рассмотрения хаоса и различных сложных движений в нелинейных системах положено логистическое уравнение. Оно может быть одномерным и двумерным. В одномерном уравнении
» X х„ (1 - х„) (П9.56)
под х„ понимают состояние системы в п интервале времени, под хн+1 — состояние системы в п + I интервале; X— некоторый параметр. Величина х в этом уравнении может изменяться в интервале 0-1, потому уравнение (П9.56) называют также преобразованием отрезка 0-1 в себя.
Двумерное логистическое уравнение может быть записано, например, в такой форме
’ 1 - а + У>,, где у,,^ = 0 х„.
Логистическое уравнение (П9.56) было известно давно, интерес к нему возрос после появления работы Фейгенбаума [38]. В ней подмечены некоторые закономерности бифуркационных процессов (процессов ветвления). При параметре X уравнения (П9.56), находящемся в интервале 1 < X < 3, в системе, описываемой уравнением (П9.56), имеются две
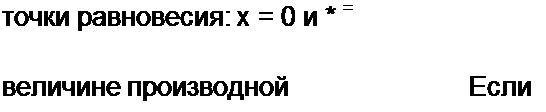 | |||||||
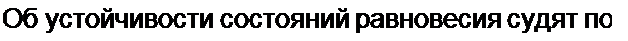 | |||||||
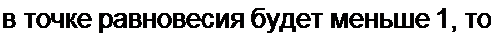 | |||||||
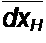 | |||||||
состояние равновесия устойчиво.
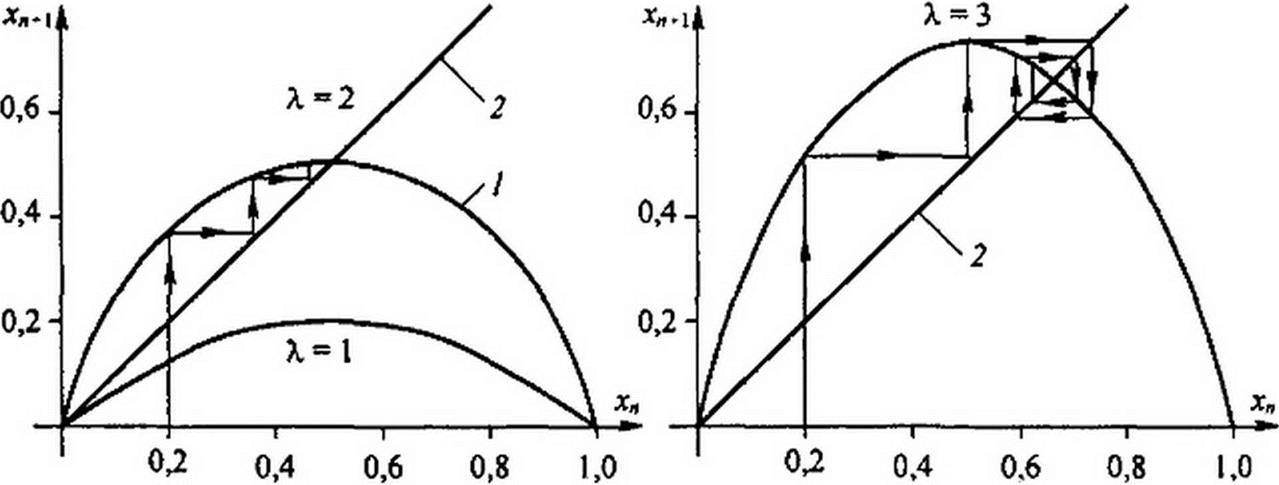
Процессы перехода от одного типа движения к другому могут быть описаны в прямоугольной системе координат x^+i = /(х„). Например, на рис. П9.10, а кривая построена по уравнению (П9.56) при X - 2. Прямая ((хя>1 - х„) описывает периодический процесс, на ней находятся точки равновесия. Стрелками показан процесс перехода от х„ к х„+| и от xw+J к х„ в этом типе движений. При X = 3 стационарный режим неустойчив, но возникает устойчивый бицикл, он окружает точку равновесия (см. рис. П9.10, б). В интервале 3<Х<4 возникают многопериодические и хаотические движения (см., например, рис. П9.10, в, на котором показана начальная часть процесса при Х = 3,5). Каждый последующий тип движения от одной бифуркации, с которой он начинается, до последующей бифуркации, которой соответствует большее X и новый тип движения, имеет удвоенный период по сравнению с предыдущим типом движений.
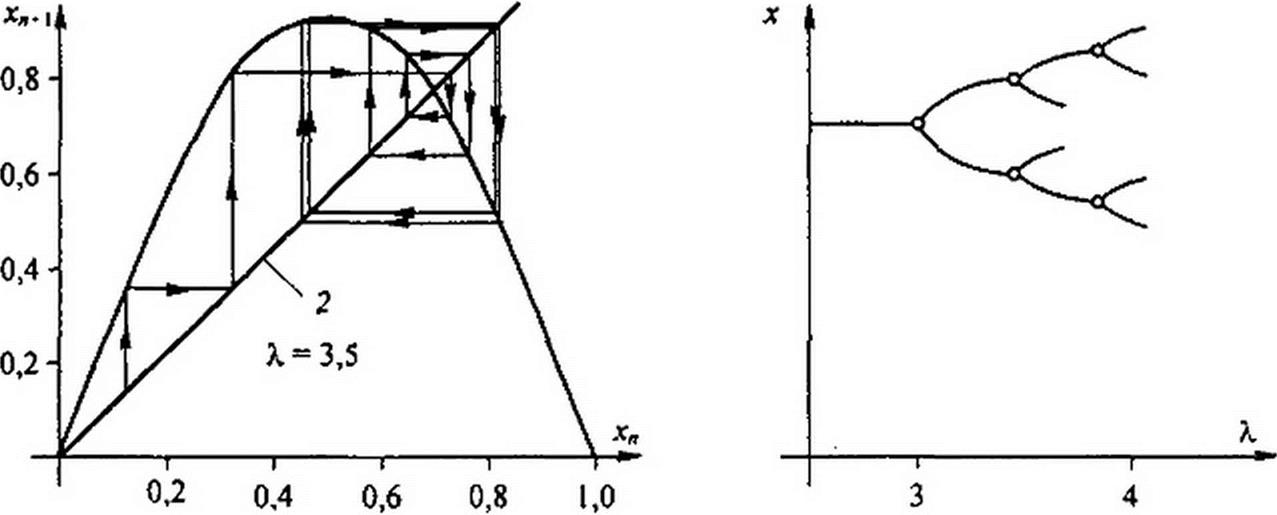
Удвоение периода будет происходить до значения Х= 3,5694. Вблизи этого значения X отношение разности параметров (Хя+| - Х„) двух последующих типов движений в разности параметров (X„-X„_j) двух предыдущих типов движений при приближении к хаосу будет стремиться к величине 1/5,, где 5 = 4,66320.
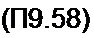 ^<iti
^<iti
Хя — Х„_(
а б
в г
Рис. П9.10
Число 8 называют числом Фейгенбаума. Если в некоторой системе, описываемой уравнением (П9.56), параметр X может достигать значений, при которых соотношение (П9.58) выполнено, то в системе возникнет хаос. В системе координат х = /(X) в интервале значений 2,9<Х<4 можно построить бифуркационную диаграмму (см., например, рис. П9Л0, г), показать на ней ветвление кривой состояний, а также области притяжения при малых возмущениях состояний случайными помехами.
Вопрос о том, насколько сценарий возникновения хаоса, предложенный Фейгенбаумом для недиссипативных слабонелинейных систем, может быть применен к реальным диссипативным существенно нелинейным системам, остается открытым — это было отмечено еще в (37). Как было показано в гл. 15 и в данном Приложении П9, возникновение хаоса и других нежелательных процессов зависит от многих факторов. Изменением одного параметра X учесть все эти факторы вряд ли возможно. В реальных нелинейных системах, рассмотренных в книге, при приближении к непериодическим процессам и во время их существования, последовательного удвоения периода по Фейгенбауму не наблюдалось.
Приложение П10








