В трансверсальных фильтрах обработка сигналов происходит по алгоритму

Дата: 2025-06-02; Просмотры: 14

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

У k =^flo +«| + ... + *«

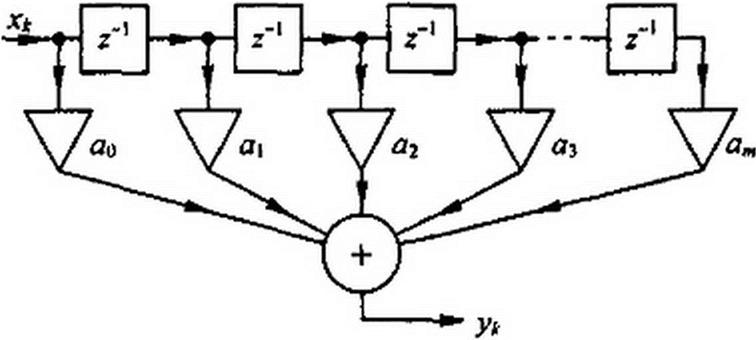
Трансверсальными их называют потому, что они содержат элементы сдвига z"', рас­положенные перпендикулярно (транверсально) по отношению к пути следования сигнала (рис. П8.4).

После учета запаздывания получим

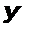= ^хк («о+01 +^₂ z’²+... + a_w z'^m).

Передаточная функция фильтра равна отношению массива Y_k к массиву Х_к

КО) = -^- = а_о z"‘ +а₂ z~² + — + z'^m. (П8.1)

^Л к

Коэффициенты а зависят от значений хЦ) в моменты дискретизации и от интервала дискретизации Т. Значения импульсной характеристики Л⁶(л) (т. е. набор единиц и ну­лей) без изменений каждый раз сдвигается на единицу вправо. Число слагаемых А⁶(я) у трансверсального фильтра равно числу т (конечно), поэтому их называют еще фильтра­ми с конечной импульсной характеристикой.

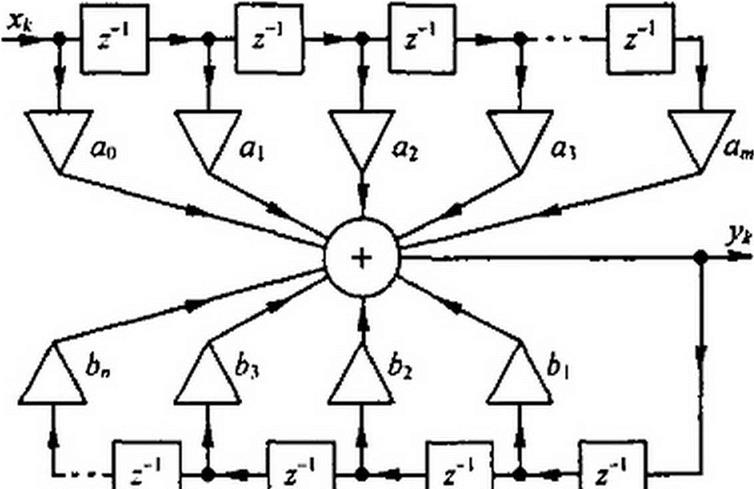
В рекурсивных фильтрах выходной сигнал создается не только последовательной со­вокупностью входных сигналов х*, х*_₂,..., как в трансверсальном фильтре, сдви­

нутых по времени, но и последовательной совокупностью выходных сигналов Ук > -Мл-1. Ук-2 также сдвинутых на свое время запаздывания. Таким образом, рекур­

сивный фильтр — это в общем случае система с многопстлевой обратной связью. Алго­ритм обработки сигналов в рекурсивном фильтре таков:

Ук ==<*0 *к +й| Jf*-1 +-. + ^m *к-т + *| Zk-| Ъ-2⁺- + ^ Ук-п-

Структурная схема рекурсивного фильтра изображена на рис. П8.4, а нижняя часть рис. П8.5 осуществляет обратную связь.

Перепишем алгоритм обработки с учетом запаздывания;

0 = хДа_о+<2) Г¹ + ... + o„ z'^w)+y*(l~^ г"¹ -b₂ z^-2z~ⁿ).

Из него следует, что передаточная функция A'(z) рекурсивного фильтра

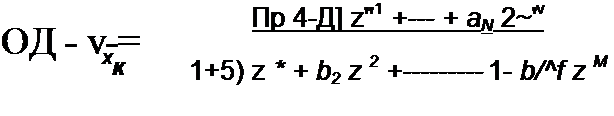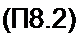Импульсная характеристика h^b(и) рекурсивного фильтра за счет обратной связи теоретически имеет очень большое число слагаемых*¹, поэтому рекурсивные фильтры именуют еще фильтрами с бесконечной импульсной характеристикой (БИХ-фильтры). В ячейках памяти рекурсивного фильтра хранятся значения предшествующих состояний х„ и у„.

‘‘Слагаемые, из которых состоит характеристика 5⁵(л) рекурсивного фильтра, полу­чим, разделив числитель формулы (П8.2) на ее знаменатель.

§ (18.4. Алгоритм получения передаточной функции цифрового фильтра. В руко­водствах по аналоговым фильтрам [И, 17] приведены таблицы полиномов знаменателя пе­редаточной функции К(р) низкочастотных аналоговых фильтров, аппроксимированные различными способами (по Чебышеву, Баттерворту, Бесселю и др.). Частота среза со_с в этих таблицах принята равной 1 (нормирована). Полиномы подсчитаны при заданном мак­симальном отклонении модуля К(р) в полосе пропускания от I и заданном затухании в полосе затухания при со = k w_c (задано к > I).

Алгоритм получения K{z) цифрового фильтра, основанный на инвариантности им­пульсной переходной характеристики, включает следующие этапы:

1. По заданным требованиям к цифровому фильтру выписываем из таблиц К(р) ана­логового фильтра, полагая, что он должен удовлетворять тем же требованиям по затуха­нию и по максимальному отклонению, что и цифровой.

м Ai

2. Если К(р) аналогового фильтра может быть представлен в виде К(р)= £—-—,

< . Р ~ Pl то переход к A’(z) осуществляют по формуле:

м

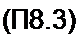
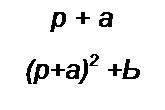
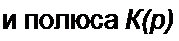= X

*=|

3. Если К{р} может быть представлен в виде р₁₂=-б±у<о₀, то K(z) цифрового фильтра

______ I ~z ¹ е~⁶⁷ cos о о Т___ 1-е"¹ 2 е”⁶⁷ cosa₀ Т + z~² е"^2Ъ1

Рассмотрим пример. Пусть аналоговый фильтр — прототип второго порядка при ап

проксимации по Баттерворту (см. § 10.11) — имеет К(р) = -—------------------------------------------------------------------------------ ---------------------------------------------------------------------------------- , корни полино

р² +-J1 р +1

ма Pi. 2 = ~^а ± J ^а-> где а = 0,707.

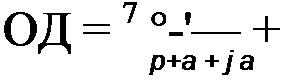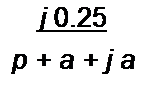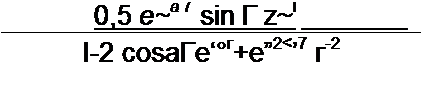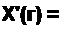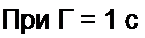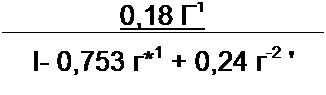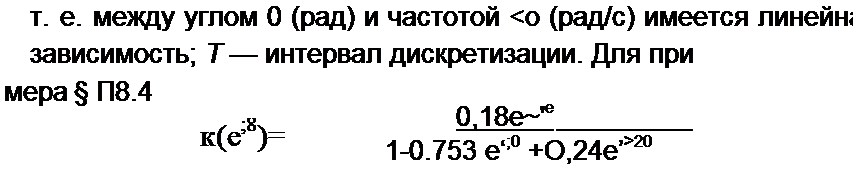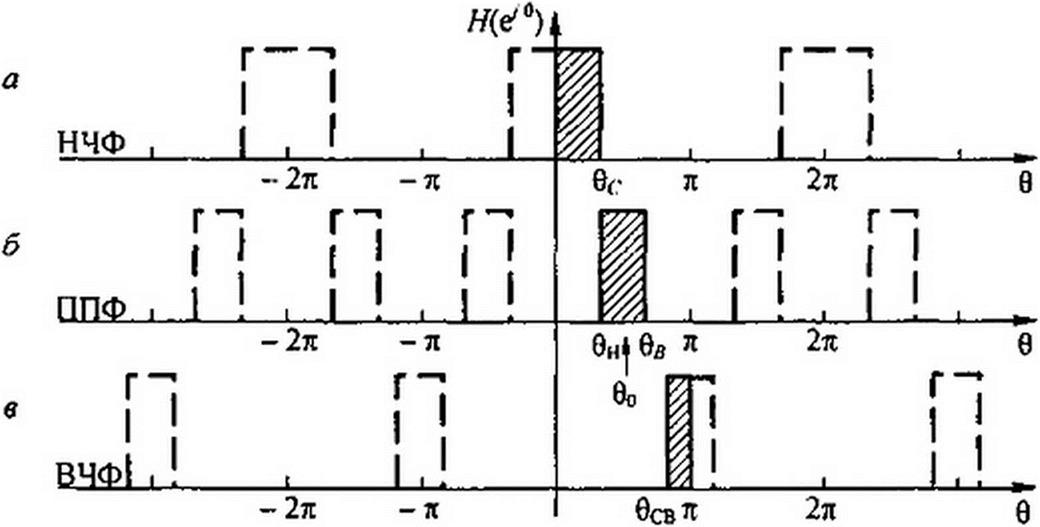
Рис. П8.7

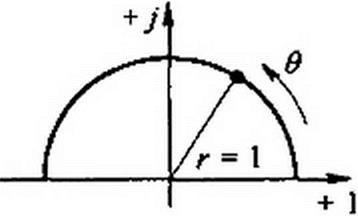
На постоянном токе (ю = 0,0 = 0) |К(г)| = 0,373. Чтобы нормализовать K(z) приме­ра, надо K(z) умножить на 1/0,373 - 2,68. В полосе пропускания НЧ фильтра 9 изменяется от 0 до о_с Т, где нормированная частота среза w_c = 1, в полосе затухания 9 изменяется от <о_с Т до 0 < л.

У аналогового фильтра НЧ имеется только одна полоса пропускания от 0 до <д_с. У соответствующего цифрового фильтра НЧ теоретически имеется несколько полос про­пускания. так как функция е^>е является периодической (е^>0 = е^{у(в+2 к я)}, где к — целое положительное число). Случай к * 0 не используется.

На рис. П8.7. а штриховкой показана полоса пропускания. Неиспользуемые полосы . . d ф(0) rt

показаны пунктиром. Групповое время запаздывания т(0) = —для цифровых филь- 4/0

трое, в основу формирования которых положено билинейное преобразование (см. § П7.8), связь й с 0 получаем так:

2 1~е"'° .2 9

P = = ---------- -т- = Jzz

Т 1 + с ^/0 Т 2

поэтому

и-ytgp (П8.6)

т. е. связь со с 0 оказывается нелинейной. Если известна частотная характеристика ана­логового фильтра К(J со), то для получения частотной характеристики соответствующе- . . .20

го цифрового фильтра в этом случае надо j <о заменить на j — tg—. 7"* 2

§ П8.6. Частотные преобразования цифровых фильтров. Подобно тому как аналоговый фильтр НЧ путем преобразования частоты (см. Приложение П6) может быть преобразован в аналоговые фильтры ВЧ, ПП и ПЗ, цифровой фильтр НЧ может быть пре­образован в цифровые фильтры ВЧ, ПП, ПЗ.

l. Преобразование НЧ ЦФ в полосно-пропускающий ЦФ. НЧ ЦФ с частотой среза = 1 надо преобразовать в ПП ЦФ с центральной частотой 0_О, верхней 0_В и нижней 0_Н. Частоты 9_о,0_в,0_н связаны уравнением

_cos0ft - ^со$(^(е» ⁺⁰и)/2)

° ’ cos((9_B -9J/2)’

m. е. две частоты из трех независимы.

K{z) ПП ЦФ получают из K(z} НЧ ЦФ путем замены

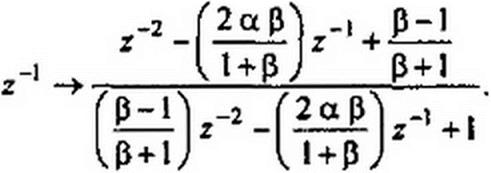
Здесь

a = cos0_o, Р =

2. Преобразование НЧ ЦФ в ВЧ ЦФ. Полагаем, что НЧ ЦФ с частотой среза 0_С надо преобразовать в ВЧ ЦФ с частотой среза 0_С8. K(z) фильтра ВЧ получают из Л’(г) филь­тра НЧ заменой

-\ , г'¹ +a _{п =} -cos[(0_c-0_ca)/2]

l + az’¹ ’ ^где cos[(0_c 4-0_св)/2] ’

На рис. П8.7, б, в заштрихованы области работы ПП ЦФ и ВЧ ЦФ (штриховой лини­ей показаны неиспользуемые области).

§ П8.7, Реализация передаточных функций цифровых фильтров. Известно несколь­ко различных способов реализации ЦФ (I1J. Рассмотрим один из вариантов так называ­емого прямого метода. Он имеет преимущества в стоимости при K(z) низких порядков.

Передаточной функции

ы

^{| +} 2>²
/-1

соответствует разностное уравнение

N М

= ^х(^п~~• (П«.8>

i=0 /я!

М

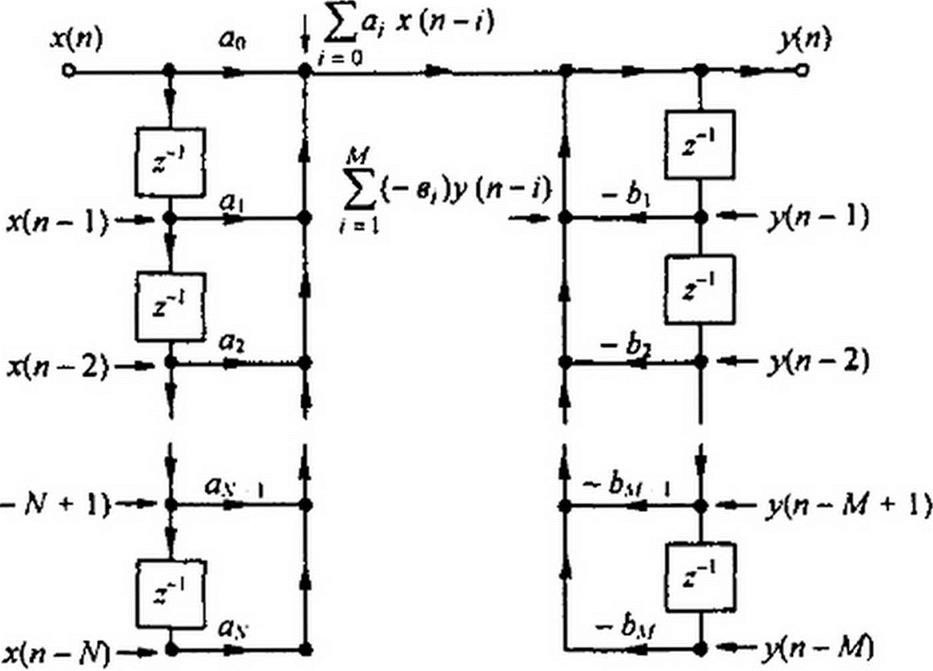
Рис. П8.8

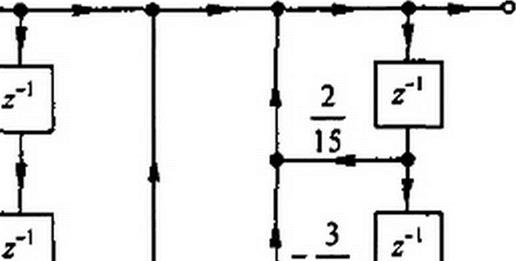
Уравнению (П8.8) отвечает схема рис. П8.8. Стрелки в узлы левой части рисунка поясняют, что сигналы х(п-1), х(л-2),... поступают в эти узлы с задержкой на Г, 2Т,... и т. д. Аналогично стрелки -► в узлы правой части схемы поясняют, что в соответствую­щие узлы сигналы v(w -1). у(п - 2),... поступают с задержкой в Т,2Т,... ит.д.

l-z'²

В качестве примера реализуем К{г) =------------- ------- ------------------------------------------------------------------------ —----- .

. Z J -2

1- — Z +— 2 *

15 15

Схема показана на рис. П8.9. Соответствие схемы на рис. П8.9 заданной K(z) прове­рим по формуле Мезона (см. § П1.1)

' ' ' Д

2

где Р_} = I, Р₂ =-1 г"¹ г^-1. Граф имеет две петли обратной связи с передачами — z'^}

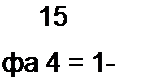Обе петли касаются прямых путей, поэтому Д₍ = Д₂ = 1. Определитель гра-

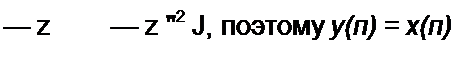l-z'²

—-------- ---------- , как и задано.

— Z ’ + —— Z

15 15

§ П8.8. Устойчивость работы цифровых фильтров. Работа рекурсивных цифровых фильтров за счет наличия в них обратной связи может оказаться неустойчивой. Рассмот­рим простой способ исследования устойчивости работы рекурсивных фильтров по вели­чине и знаку коэффициентов 2>_|( b₂, b_it... знаменателя его передаточной функции К(г) (формула П8.2).

Исходим из того, что рекурсивный фильтр сформирован по его аналоговому прототипу. Способ исследования будем иллюстрировать простым примером. Пусть знаменатель K(z) рекурсивного фильтра равен 1 ~b_t z‘^l -b₂ z~². Поступаем так: перепишем знаменатель

и приравняем его нулю. Определяем численные значения корней уравнения z² -Ь_х z~b₂ = 0. Они равны

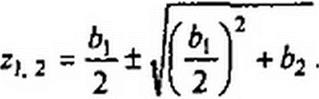Далее исходим из того, что полюсы аналогового прототипа р_х и р₂ и полюсы z_t и z₂ цифрового связаны соотношением

2 .

Pk =у

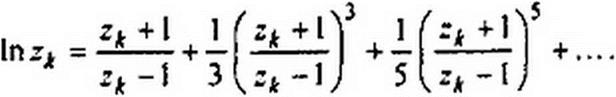Ряд для In z_k сходится очень быстро, так что можно ограничиться первым членом ряда, и потому положим pi, = —

Множитель 2 / Т в последнем выражении больше нуля и потому он не влияет на вопрос о том, в левой или в правой части плоскости р оказываются корни р_к. Поэтому вместо комплексной плоскости р будем проводить исследование устойчивости с помощью 2

комплексной плоскости р' = — р. Координаты точек плоскости р' будут равны координатам точек плоскости р, умноженным на Г/ 2.

Далее будем оперировать с плоскостью р' и с плоскостью z. Координаты точек р\ и z_k этих плоскостей связаны двумя взаимно-обратными преобразованиями:

Р’к = ^4 (П8.9)

z* -1 И

г*=-4~- (П8.10)

Рк "I

Формулу (П8.10) получим, если решим (П8.9) относительно z_k.

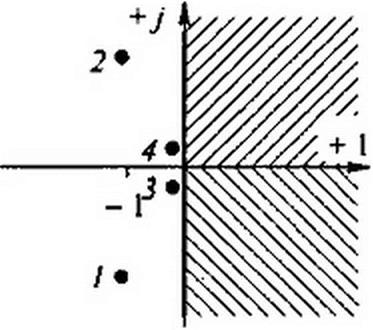
Рассмотрим соответствие точек плоскости р' с точками плоскости г (см. рис. П8.10). Точке р\ =-1 соответствует точка г* =0 (тс. начало координат плоскости г). Мнимой оси плоскости р\ т. е. величине р' - j к (где к — действительное число) соответствует

Рис. П8.10

окружность единичного радиуса на плоскости г. Действительно, точки этой окружности будут описываться выражением

_jk + l Jl + Pc-'"*»*

j k -1 ₊ c^{J (x-arc,}s*>

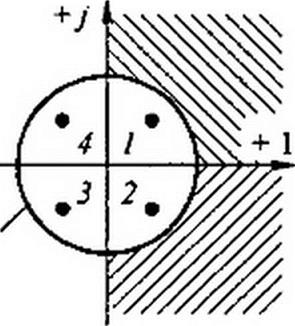
Точки, обозначенные цифрами /, 2, 3, 4, лежащие внутри окружности единичного радиуса на рис. 3.10, б, соответствуют точкам J, 2, 3. 4 на рис. П8.10, а, лежащим в левой части плоскости р'.

Точка 1 г, =0,5 + у 0,5. Ей соответствует р'_} = 2,242 е^-71,7 .

Точка 2 z₂ = 0.5 - j 0,5. Ей соответствует р₂ = 2,242 е⁷¹¹⁷ .

Точка 3 z₃ = -0,5 + j 0,5. Ей соответствует р'₃ = 0,445 е“⁷¹¹⁷ .

Точка 4 z₄ = -0,5- у 0,5. Ей соответствует р\ = 0,445 е⁷¹¹⁷ .

Верхней части правой полуплоскости р’ (см. одинаковую штриховку на рис. П8. 10, а и б) соответствует нижняя, а нижней части правой полуплоскости соответ­ствует верхняя часть правой полуплоскости г.

Таким образом, если все полюсы z_k K(z) окажутся внутри единичной окружности на плоскости z, то работа рекурсивного цифрового фильтра будет устойчива (подобно тому

как будет устойчива работа аналогового фильтра прототипа, у которого все полюсы будут в левой полуплоскости р').

Если же хотя бы один полюс z_k окажется не внутри, а снаружи единичной окружно­сти на плоскости z, то работа рекурсивного цифрового фильтра будет неустойчива, и надо будет изменить интервал дискретизации Г, чтобы работа фильтра стала устойчивой (от величины Тзависят модули и знаки коэффициентов dj,6₂,... в знаменателе K(z)).

В качестве примера рассмотрим два случая, в первом примем, что b_} = -I и Л₂= 0,5, во втором, что = -!, b₂ = -0,5. По (П8.9) и (П8.Ю) в первом случае г_х =0,366 и z₂ - -1,366 (при этом р\ = -2,154 и р'₂ = 0,154) — работа цифрового фильтра будет не­устойчива. Во втором z_t = -O,5 + jO,5 и z₂ = -O,5-yO,5 (при этом р\ =0,445e~^{J 117} и р₂ = 0,445 е^{у 117} ) — работа цифрового фильтра будет устойчива.

Если полином знаменателя K(z) будет иметь не второй, а третий или четвертый поря­док, то корни его после небольших преобразований определим через радикалы. При пятой и более высоких степенях полинома знаменателя корни придется определять с по­мощью ЭВМ.

В заключение отметим, что в рекурсивном фильтре при определенных условиях воз­можно возникновение своеобразного автоколебательного процесса: выходной сигнал y{t) возникает при отсутствии входного сигнала x(t) на входе фильтра. Такой процесс в филь­тре может возникнуть, если в ячейках памяти фильтра сохранены значения величин х(п) пу(п) предшествующего режима работы фильтра, если часть полюсов K(z) находится вне окружности единичного радиуса и если действует генератор импульсов синхронизации.

Приложение П9