Для цифрового входного сигнала вместо Х(р) будет X(z). Поэтому передаточная функция цифрового четырехполюсника (системная функция цифровой системы) на рис. П7.2. б
(П7.8)
Составим K(z) примера, описывающего разностное уравнение (П7.4). В соответствии с формулой (П7.7)
у(м-0->-‘1 Y(z\ y(n-2)->z'2 Y(z), x(n)->X(z).
Уравнение (П7.4) запишем так:
 |
|
 |
|
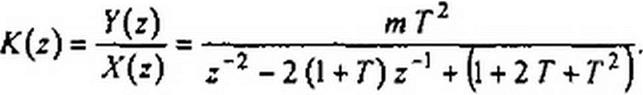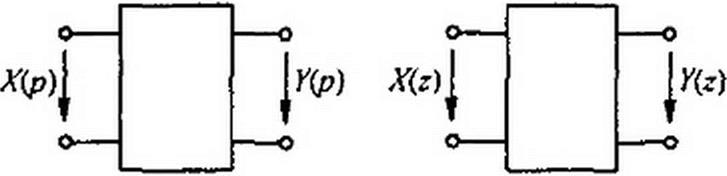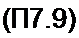§ П7.6. Обратное Z-преобразованне. Обратное Z-преобразование осуществляют по формуле
*(*) =
Контурный интеграл берегся по замкнутому пути С в области сходимости функции
Х(г) на плоскости г. Формула (П7.9) — это аналог формулы обратного преобразования
Лапласа:
х(г) = т—Х{р)ър‘ dp. 2* J Je
Известно, что нахождение оригинала х(/) по изображению осуществляют обычно не путем взятия контурного интеграла, а более простым путем, разлагая Х(р) - \'(р)/М{р) м л
на сумму простых дробей (см. §8.49), т. е. Х{р) = \----------- — корни уравнения
. *=i Р ~ Pk
-
А/(р) = 0), и затем, учитывая, что —-—= Ак , получаем
Р~Рк
(П7.10)
Аналогично поступают и при обратном Z-преобразовании. Функцию A'(z) записывают в виде
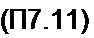У
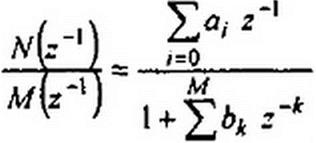
и находят корни z 1 знаменателя A/(z"j=0. Положим, что все они действительны и различны. Тогда А'(г) можно представить суммой простых дробей
 | |||||
 | |||||
 | |||||
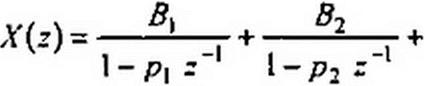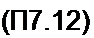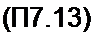= Res Ar(z) = (l-pt z’l)^(zX . '-=Р*
Переход от А'(х) к цифровой функции времени x(w) осуществляют с помощью соотношения аи и(п)-* -—г (см. § П7.1). В результате получим
1-47Z'1
х(л) = (в1 р'\ + В2 р2 +“■ + Вмрм)и(п). (П7.14)
 | |||||||
 | |||||||
 | |||||||
 | |||||||
 |
 |
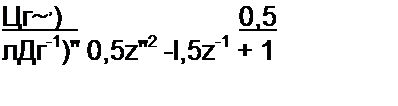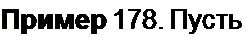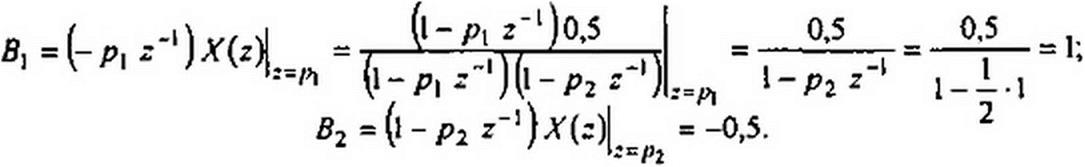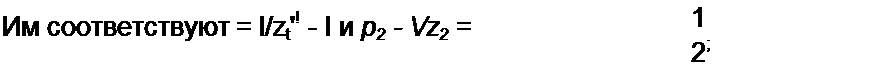Отсюда xV(z) =------------------------- ——г- По формуле (П7.14) цифровая функция време-
1-lz’1 l-0,5z”1
ни х(п) = (1 -0.5 0.5")«(«) = 0,5; 0,75; 0,875; 0.9375;....
Если среди корней уравнения A/(z~')=0 будет два комплексно-сопряженных корня: =а + у0 и рг=а-/р, то и коэффициенты Bq и Вг будут комплексно-сопряженными [Bq -т + j q, Br =т- j q). Этим корням в формуле (П 7.14) будет соответствовать вещественное слагаемое
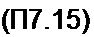Bq Pq + Br р'‘ = 2 |SG Upd" cos(v + n ф);
v = arctgg//n, 9 = arctg0/a.
Если знаменатель X{z) в формуле (П7.11) будет иметь корень zr - рг кратности г, то соответствующее этому корню слагаемое в формуле (П7.14) определим как вычет фун
кции X(z) в кратном полюсе
 | |||
 | |||
 | ||
 | ||
 | ||
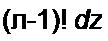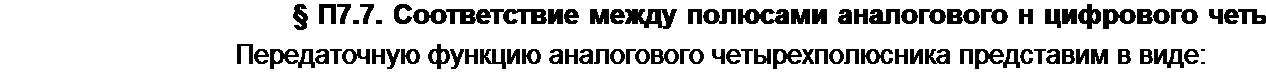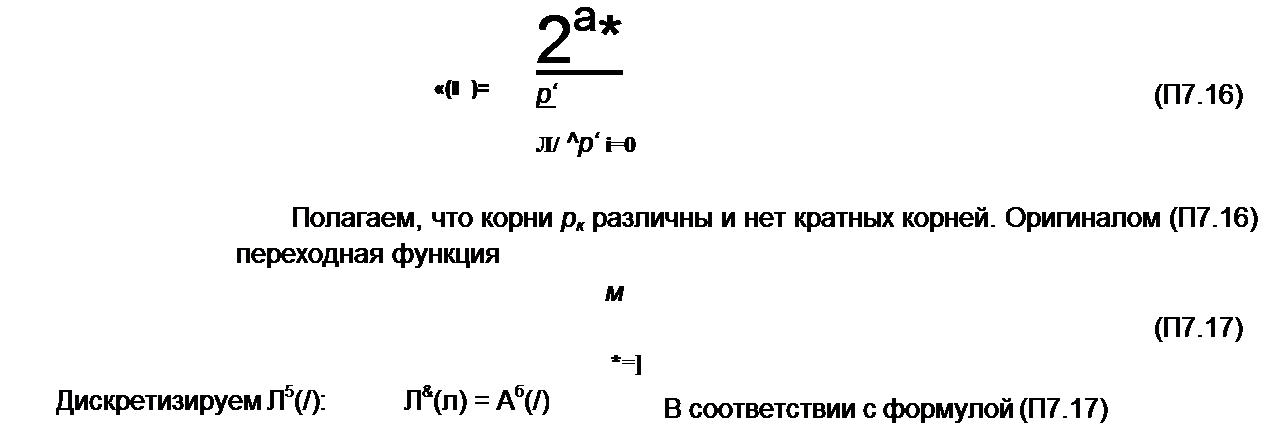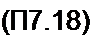Л6(л) = £ Л е? кпГ.
ы
Для нахождения передаточной (системной) функции цифрового четырехполюсника подвергнем Л$(л) Z-преобразованию
х fy) М х М
//=0 и=0*=1 л=0Л=1
 |
|
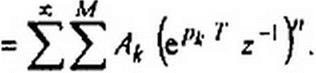Но, по формуле (§ П7.1),
 | |||||
 | |||||
 | |||||
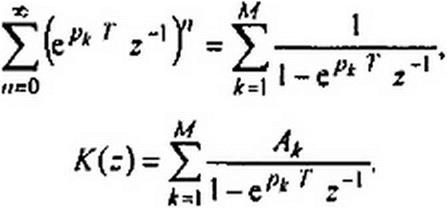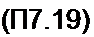Сопоставляя (П7.16) и (П7.18), получаем соответствие
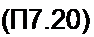I f 1
Р-Рк l-ePt ? z’1
Таким образом, полюсу рк аналогового четырехполюсника отвечает полюс еЛ Т цифрового.
| § П7.8. Переход от передаточной функции аналогового четырехполюсника к передаточной функции соответствующего цифрового. Известны два основных способа перехода. В первом в К(р) = V -— каждый член суммы заменяют на ---------------------------------------------- г—г- в tZP-Pi 1-еЛ'Г’ соответствии с (П7.20). Этот метод называют методом инвариантности переходной характеристики. Второй метод — метод билинейного преобразования состоит в том, что в К(р) за- 2 1-z'1 меняют р на----------------- Эта замена может быть обоснована так: возьмем натуральный ло- Т l + z~_ гарифм равенства cr = z. Получим pf = inz. Разложим Inz в ряд и возьмем первый |
| член ряда In z = 2 |
| Z-1 |
| ~ 2 z-l 2 1-z"1 . Отсюда р = -------------------------------- |
| Рассмотрим эти методы на примере. • Д р —7 Пусть у аналогового прототипа К(р) = --------------------------- г =-------- (р + 1)(р + 3) р + 1 Согласно первому методу, |
| 1 -I .-I ,.-4Г -2- I — С Z | + с Гх т с Z |
| По второму методу |
| 6____ 2 1-2~‘ т I . |
| 1-Z-2 |
| (2 + Г)(2 + ЗГ) । 6Г-4 _i '(2 +Г) (2+ 3 7) Z |
| 4-87~ _2 (2 + Г) (2 + 3 Г) 2 |
Приложение П8
Цифровые фильтры
§ П8.1. Введение. На рис. П8.1 изображена структурная схема цифровой обработки сигналов. Аналоговый сигнал x{t) поступает на аналого-цифровой преобразователь (АЦП). Он выполнен в виде микросхемы и является типовым элементом электроники. Сигналы, поступающие на вход цифрового фильтра, записывают в виде совокупности следующих друг за другом единиц и нулей, выражающих степени числа 2. Например, запись 11100 соответствует сигналу 1-2° +1-21 + 1-22 +0-2J +0-24 -12° +1-21 + )-22 или, иначе, сигналу 1 + z~l + z"2. С выхода АЦП цифровой сигнал х(л) поступает на цифровой фильтр, где осуществляется цифровая фильтрация. Сигнал с выхода фильтра у(п) поступает либо в цифровом виде, либо, как показано на рис. П8.1, в цифроаналоговый преобразователь (ЦАП — своя типовая микросхема), который преобразует у(п) в y(t). Цифровая обработка сигналов применяется уже свыше 40 лет в системах связи, радио и гидролокации, медицине, разведке полезных ископаемых и для других целей.
АЦП ЦФ ЦАП
Рис. 118.1
Цифровая обработка сигналов осуществляется двумя способами, которые условно называют аппаратурным и программным. Аппаратурная обработка рассмотрена в Приложении П8. Программная осуществляется с помощью специальных программ на ЦВМ с относительно большим объемом памяти, реализующих прямое и обратное дискретное преобразование Фурье и дискретную свертку. Ее основные положения рассмотрены в Приложении П5 (без программ для ЦВМ).
Программная реализация подробно рассмотрена, например, в [17].
§ П8.2. Элементная база цифровых фильтров. Аналоговые фильтры, как известно, состоят из элементов L, С, R, а в некоторых случаях еще и из управляемых источников. Цифровые фильтры состоят совсем из других элементов, а именно:
а) элементов г-1, осуществляющих единичные задержки на один такт Т (регистры сдвига для хранения предыдущих значений входных и выходных сигналов), обозначают их в соответствии с рис. П8 2, а;
б) умножителей, которые выполняют умножение или масштабирование. Их обозначают, как показано на верхнем и нижнем рис. П8.2, б;
в) сумматоров (они же могут выполнять и вычитание), обозначают их в соответствии с верхним или нижним рис. П8.2, в. Места соединений элементов (узлы) обозначают точками. Если на схеме фильтра не записана величина передачи на линии, соединяющей узлы,
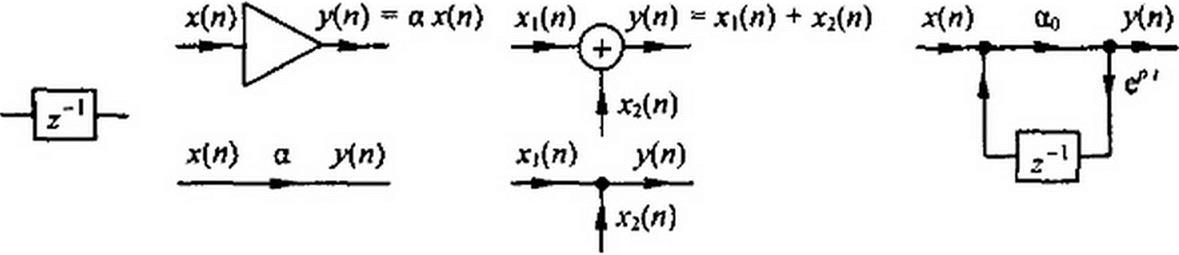
а б в
 |
то она принимается за 1. В качестве примера на рис. П8.2, г изображена схема цифрового фильтра, для которого К (г)------------------------------------- а—------- .
1-п0 ер,г~'
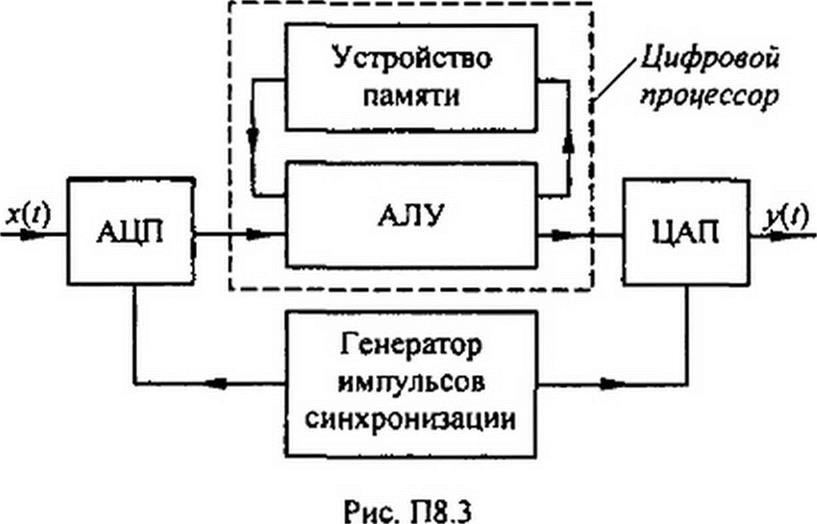
Более полно взаимодействие и последовательность работы отдельных блоков цифрового фильтра иллюстрирует рис. П8.3. На нем изображены АЦП, ЦАП, генератор импульсов синхронизации и цифровой процессор, состоящий из устройства памяти и арнф- метическо-логического устройства (АЛУ).
Аналоговый сигнал х(() поступает на вход АЦП. Им управляет генератор синхронизирующих импульсов. В моменты подачи импульсов на выходе АЦП возникает последовательность либо коротких импульсов, соответствующих мгновенным значениям х(/) в порядке их образования в последовательном коде, либо совокупностей уровней напряжения на сигнальных шинах уровней разрядов в параллельном коде.
АЛУ умножает, складывает и сдвигает сигналы на заданное число интервалов времени в соответствии с алгоритмом обработки сигналов.
Цифровой процессор преобразует последовательность поступающих в него чисел в последовательность двоичных чисел. ЦАП переводит эту последовательность в аналоговую форму y(t).
§ П8-3. Классификация цифровых фильтров. Цифровые фильтры разделяют на трансверсальные и рекурсивные.