Z-преобразование цифровых сигналов
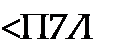
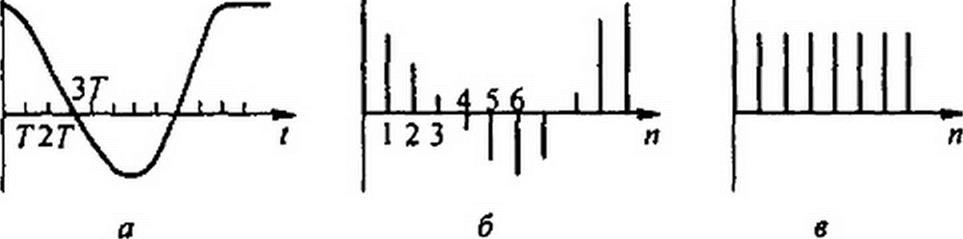
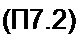§ П7.1. Прямое /-преобразование цифровых сигналов. На рис. П7.1, а изображен некоторый аналоговый сигнал, а на рис. П7.1, 6 — соответствующий ему цифровой сиг* нал, заданный последовательностью ординат х(п /), или Проше х(п):
х(п) =... х(-1), х(0), ХО. - •
Эту последовательность в общем виде можно представить суммой:
Ф) =
/(«-•Л
Здесь 8(п - к) — единичный импульс (площадь его равна 1) при п = к-, 5(п - к) = 1 и 8(и-*) = 0 при п*к (функцию Ь(п-к), обладающую таким свойством, называют функцией Кронекера). Переход от аналогового сигнала x(t) к цифровому х(л) осуществляют с помощью цифрового преобразователя (АЦП), который выполняют в виде микросхемы. Он является типовым элементом электронных схем.
Подобно тому как непрерывный аналоговый сигнал x{i) может быть подвергнут прямому преобразованию Лапласа (гл. 8): функция х(п) может быть подвергнута прямому /-преобразованию:
*(’)* "■
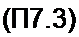>1=0
Суммирование начинают с » = 0, полагая, что х(п) равно нулю при п<0.
Последовательность единичных импульсов, возникающих при л = 0,1,2,... (рис. П7.1, в), принято обозначать и(п). При п£0 ц(п)=1.
Степенной ряд х(п) = а" при я>0 а* .а1 .а2.... с помощью функции и(л) может быть записан; х(л) = а" и(и). Линейно нарастающую функцию х(п) = 0,1,2,3.... представим так x(n) = и и(п).
Под радиусом сходимости функции Х(г}, представляющей собой ряд по отрицательным степеням г. понимают радиус области комплексного переменного z с центром в начале координат, лежащей вне окружности радиуса R.
/-преобразование совокупности импульсов рис. П7. },в осуществляется функцией
/V(z) = —— =— • = I + z 2 + с 2 +... (Л = 1).
г-1 1-z4
 |
| ||||
| ||||
Z-преобразовакие стеленного ряда Х(п) = = 1 + п + <я2 +а3 +... осуществляется
< //=0
функцией X(z} = —-— ----------------- r = l + az“’+fl2z'2+a)z'}+„. (Я = |а|).
z-a l — az
Z-преобразование линейно возрастающей функции Х(п) = п и(п) производит функция
-I х2
Z-преобразование дельта-функции 8(л) осуществляет функция X(z) = l {Я = 0).
Z-преобразование Ь(п-т) осуществляет функция X(z)-z~m (Л = 0).
Z-преобразование синусоидальной функции времени выполняется функцией
Лг)= z-'smcp ---------------------- (Я = 1)
г -2 z coscp +1
/-преобразование косииусоида,1ьной функции времени выполняется функцией
2 ~2z С0$ф+1
§ П7.2. Решение дифференциальных уравнений путем сведения их к разностным. Линейному дифференциальному уравнению с постоянными коэффициентами может быть сопоставлено разностное уравнение.
Первая производная по времени от непрерывной аналоговой функции y(t) может быть аппроксимирована конечной разностью
<*Х')| Х«)“Х«-0 м dy(t) _ у(и-1)~у(и-2)
d( lsttr ? dt Т
Вторая производная
 |  | ||||||
 | |||||||
 | |||||||
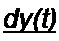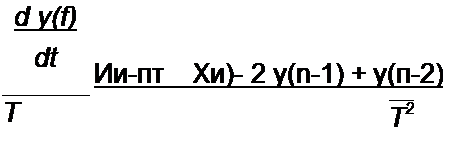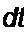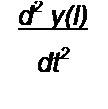Аналогично определяют производные и более высоких порядков.
d2 yft) d y{t) _
В качестве примера запишем уравнение —+ 2--------------------------------------------------------------------------------- -+3 y\t) = т x\t) с началь-
dr dt
ными условиями у(0-) = 0 и составим соответствующее ему разностное уравнение:
у{п)-2у(П-^у(п-2) + 2 Ил)-Я»-1> + зХл)гяХя) т2 т
или
у(п} (| + 2 Г + 3 Г2)- у(и -1) (2 + 2 Г}+X» - 2) = Г2 m х(п). (Л7.4)
По уравнению (П7.4) можно последовательно определить знамения Xя). придавая значения п сначала 0, затем 1, 2,3,... и т д., и учитывать при этом, что у(-1)= у(-2) = 0, а х(О), х(1), х(2),... известны.
Рассмотрим пример. Пусть в (П7.4) Т = 1, m = 1, х(0) = h х0) = 2, х(2) = 3 и т.д. Тогда уравнение запишем так:
6 Х«)_ 4 у(п -1) + Хи - 2) = х(л),
при л = 0 6ХО)-4 О + О = Х0) = 1. отсюда у(0)=]/6, при л = 1 6у(1)-4у(0) + Х”1) = Х1) = 2, находим Х0 = 4/^> при п = 2 6Х2)-4Х1) + ХО) = Х2)=3, следовательно, у(2) = 83/18 и т. д.
§ П7.3. Дискретная свертка. Положим, что при нулевых начальных условиях на вход некоторого аналогового четырехполюсника (рис. П7.2, а) воздействует аналоговое напряжение «|(г) = х(г), а импульсная переходная функция четырехполюсника (реакция
на импульс единичной плошади в виде 6-функции) /т5(/) известна. Тогда напряжение на выходе четырехполюсника w2(/) = y(t) определим по одной из форм записи интеграла
Дюамеля: у(0 = fх(т)Аб(/ или у0) = |х(/-х)А6(т)й/т (полагаем х(/) = 0 и
о о
hb (/) = 0 при {< 0). Аналогом этих формул, когда сигнал взят в цифровой форме, являются формулы:
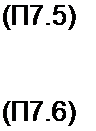£х(*)лб(*-*);
к^
y(.n)^^x(n-k)hb(k).
*=0
§ П7.4. Теорема смещения для цифрового сигналя. Если x(t)~ 0 при t < 0, то изображение по Лапласу аналогового сигнала х(/) = Х(р) и в соответствии с теоремой смещения (см. § 8.40) изображение функции х(/ -/0) = e'F'n Х(р).
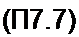Аналогично,если последовательность х(л) (при п<0 х(п) = 0) соответствует X(z\ то последовательности А'(и-1) будет соответствовать г-1 Д'(г), а последовательности
х(п- т)-> г~т X(z).
Формула (П7.7) следует из (П7.3) с учетом того, что функция х(я-/л)= 0 при л <0.
Таким образом, умножение функции X(z) на z~m означает задержку ее на т интервалов дискретизации Т.
§ П7.5. Передаточная функция цифрового четырехполюсника. При использовании преобразования Лапласа для аналогового сигнала передаточная функция четырехполюсника (рис. П7.2, а) на комплексной частоте р К(р)= Y(p)/X(p).
Передаточную функцию для синусоидального процесса получаем, заменяя р на j со