Частотные преобразования

Дата: 2025-06-02; Просмотры: 13

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

§ П6.1. Классификация частотных преобразований. Известны два основных направ­ления частотных преобразований электрических цепей. Первое направление объединяет преобразования, которые позволяют от некоторой исходной схемы (схемы прототипа) — частотные свойства которой изучены — путем преобразования частоты перейти к некото­рой другой (преобразованной) схеме с новыми элементами и с новыми частотными свой­ствами, сравнительно легко получаемыми из частотных свойств исходной схемы. В пер­вую группу входят частотные преобразования первого и второго рода, нашедшие широ­кое применение. Второе направление основано на преобразовании Брутона. Оно состоит в том, что сопротивления всех элементов исходной схемы делят на комплексную часто­ту р. При этом элементы Л, L, С исходной схемы заменяют на элементы С, R, D преобра­зованной схемы соответственно. Частотные свойства каждого элемента, естественно, изменяются, но частотные свойства всей схемы остаются без изменений. Преобразование позволяет избавиться от индуктивных элементов, элементов громоздких и с большой массой. Преобразование используют в теории фильтров.

§ П6.2. Частотные преобразования первого рода. Их осуществляют, заменяя комп­лексную частоту р в исходной схеме на некоторую функцию комплексной частоты 5.

Рассмотрим три примера. В первом из них заменим р на со_о/5, во втором — на , J² +(Oq □ s _ _с

к---------- —, в третьем — на ---------- ■——т-. Первое преобразование дает возможность перей-

«о⁵ к(5^г+Ц)о)

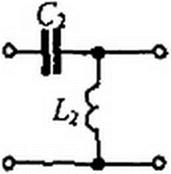
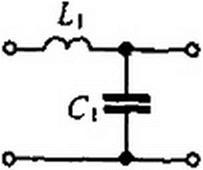
ти от схемы, хорошо пропускающей низкие частоты (например, от схемы рис. П6.1. а), к схеме, хорошо пропускающей высокие частоты (рис. П6.1, б)\ — некоторый масштаб­

ный множитель. Элементам и С₍ схемы на рис. П6.1, а отвечают соответственно С₂ и Л₂ схемы на рис. П6.1, б. Для выявления связи Ц и С₍ с С₂ и L₂ запишем сопро­тивление элемента на частоте р, заменим в нем р на <o_o/s и сопоставим его с сопро­тивлением элемента С| на частоте з. В результате получим р L\ =<о_о L\l^s =

отсюда С₂ - 1/((D_O L,). Поступая аналогично по отношению к С] и £₂, имеем !/(/? C_t) = s/(w₀ C_}) = sL₂, следовательно, £₂ = 1/(ы₀ Cj).

Передаточная функция преобразования схемы рис. П6.1. б

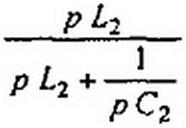может быть получена из передаточной функции непрсобразованной схемы на рис. П6.1, а

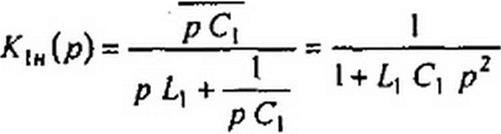заменой

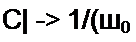P-*43q/s, £| -> 1/((О_о С₂),

Из равенства К_2п(5)= К_1н (со_о/^) следует, что схемы на рис. П6.1, а, б имеют одина­ковые частотные характеристики, только направление отсчета частоты по оси частот для преобразованной схемы рис. П6.1, б противоположно направлению отсчета частоты для исходной схемы рис. П6.1, а.

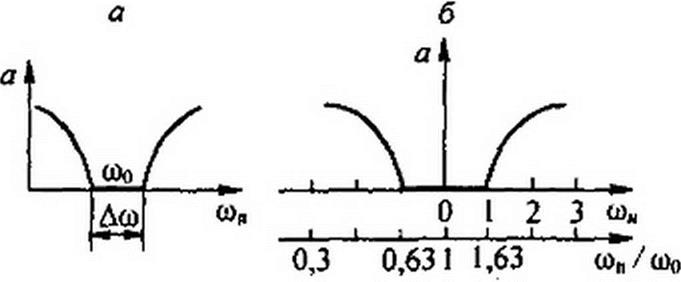
Если по оси частот на рис. П6.1, в частота о_н для исходной схемы на рис. П6Д, а (р = J откладывается в равномерном масштабе и отсчитывается слева направо, то зависимость затухания или передаточной функции преобразованной схемы изображается

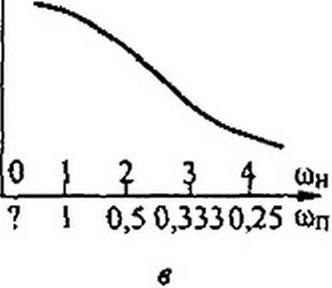Рис. П6.1

той же кривой, что и для исходной схемы, только частота для преобразованной схемы <о_п (s = j w_n) по оси абсцисс откладывается в неравномерном масштабе <в_п = хо_о/<о_п (это следует из соотношения p = &q/s или j о_н = <о_о/j ю_п = -j со₀/со_п). Знак минус означа­ет изменение направления отсчета частоты о_п по сравнению с направлением отсчета частоты ф_н.

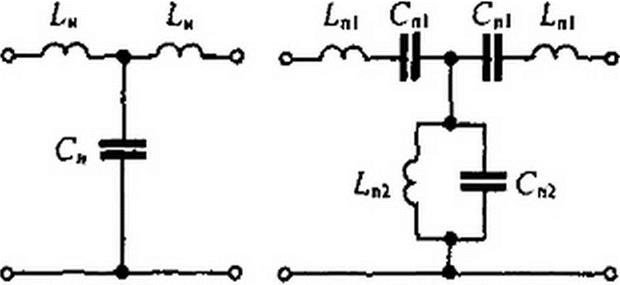
В качестве примера на рис. П6.1, в дана оцифровка по оси абсцисс для частот ю_н и со_п при «о=1. Преобразование фильтра низких частот (ФНЧ) рис. П6.2, а в по- лосно-пропускаюший фильтр (ППФ) рис. П6.2, б осуществляется заменой р на <p(j) = ^(f² +й)о//(у_о j. Положим, что параметры ФНЧ (£_н и С_н) известны, а также из­вестна желаемая резонансная частота о_п рис. П6.2, в и полоса пропускания До ППФ. Частотная характеристика ФНЧ рис. П6.2, г может рассматриваться как частотная харак­теристика ППФ при правильной оцифровке по оси частот на рис. П6.2, г для этого филь­тра и определения значений £_ftt,C_ni,L_n2 и С_п2 через £_н,С_н.Дсв и <л₀. Индуктивному элементу £_н при переходе от схемы ФНЧ к схеме ППФ соответствуют последовательно соединенные £_п1 и C_nt, а емкостному элементу С_н—параллельно соединенные £_п2 и

С_п2. Для того чтобы выявить соответствие между £₀₎,С_п1 и £_и, в выражении для со­противления р L_H заменим р на к (г² ч- coq )/со₀ 5 и сопоставим полученную формулу с

формулой для последовательно соединенных £_п| и С_п) на частоте 5:

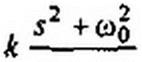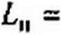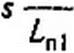Рис. П6.2

Из сопоставления следует, что L_n) - к С_п) = 1/(к со_о £„).

Поступая аналогичным образом для перехода от С_н к параллельно соединенным £_п2 и С„2> найдем

i

1 _ <Д0 — *~п2

Р С_ц к(з^г +СОо)с„ / ₊ .. ¹ ..

^п2 С_П2

Отсюда L„2 = \/[к (О₀ С_и), С_п2 = С_н к ы₀.

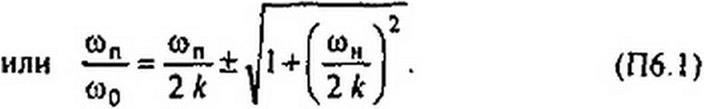
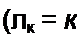Для оцифровки оси абсцисс частотной характеристики преобразованной схемы сле­дует выявить соответствие между частотами ш_н и <л_п. С этой целью в выражении р = к (s² + Wq)/ii)₀ 5 следует заменить р на j w_H, a з на J аз_п и решить полученное урав­нение относительно й)_п;

“о ^WnJ

Из (П6.1) следует, что оцифровка по оси %/гоо неравномерна. Частоте о_н -0 соот­ветствует <о_п /<о_о «1. Два знака перед радикалом в (П6.1) указывают на то, что частотная характеристика ППФ имеет две ветви, одна из которых будет являться зеркальным отра­жением другой относительно вертикали, проведенной через точку о_п/<о₀ = 1.

Придавая <д_н отрицательные значения, получим повторение частотной характеристики преобразованной схемы в области отрицательных частот, т. е. при частотном преобразо­вании характеристика может оказаться повторенной. На рис. П6.2, г оцифрована ось и_п/а>о для полосно-пропускающего фильтра при к = ю₀/Да = 1.

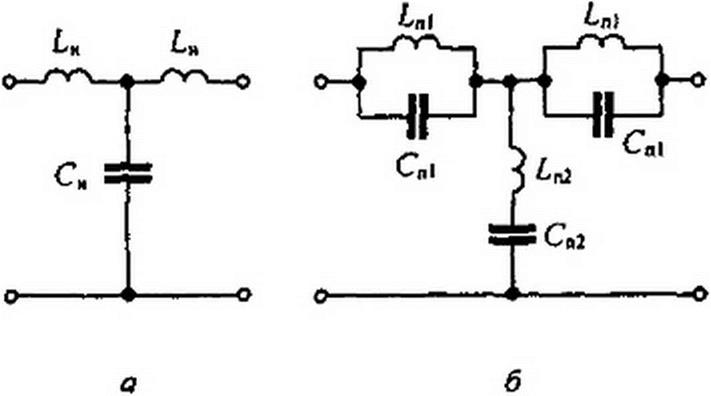
Преобразование ФНЧ рис. П6.3, а в полосно-задерживающий фильтр (заграждающий ПЗФ) рис. П6.3, б осуществляется заменой комплексной частоты р на А ?

_. и заменой £_м на параллельно соединенные £_П| и С_п1. а со_о 3 ) k[s² +Wo)

С_и — на последовательно соединенные L_n2 и С_п2 ■ Под понимают резонансную час­тоту, а под До— ширину полосы затухания (рис. П6.3. в) к = <о₀/Д со. Для определения значений £_я|,С_пЬ£_п2 и С_п2 через £_Н,С_Н,А и и₀ надлежит сопротивление р£_н заме-

нить на —т-^—£_н и сопоставить его с сопротивлением параллельно соединенных £_nJ к + Wq)

и С_П| на частоте $:

s

^ю0 ⁵ г

4²_+в1) , । •

^п! С_п1

Получим £_п) = L_M/(A q₀), C_ni = £_и).

I 5²+<I)q

для нахождения £_п2 и С_п2 сопоставим сопротивление —— =---------------------------------------------------------------------------------- ссопротив-

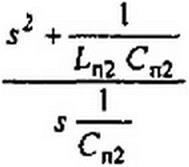К соо _с к ^н лением последовательно соединенных L_n2 и С_п2 по частоте $:

^■С s к "

отсюда Д_п2 = А/(®о ^Ск)« С„₂ = С*/(^к со₀).

С целью получения соответствия оцифровки по оси абсцисс на частотной характери­стике ФНЧ с оцифровкой по оси абсцисс на той же частотной характеристике, но для ПЗФ,

©о s

—тт заменим р на / со_м, а $ на j
2 2 fl * v* П ’ аЛ И

В результате получим уравнение

Решим его относительно (о_п/<в_о

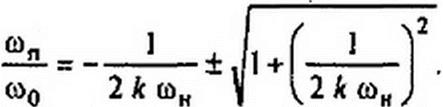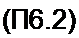Формула (П6.2) позволяет осуществить оцифровку оси абсцисс на частотной характе­ристике ФНЧ для ПЗФ.

В заключение рассмотрим свойства преобразования, при котором р заменяют на <p(s) = 1/($ + л). В этом случае индуктивный элемент индуктивностью L заменяют на па­раллельное соединение конденсатора емкостью С -\jL и резистора сопротивлением R - I/а, а конденсатор емкостью С — на последовательное соединение резистора сопро­тивлением R = ajC и индуктивного элемента индуктивностью L = l/C.

§ П6.3. Частотные преобразования второго рода. Частотное преобразование второ­го рода представляет собой преобразование, состоящее из двух операций: замены комп­лексной частоты р для сопротивлений исходной схемы на некоторую функцию ф(^) комплексной частоты 5 и умножения всех сопротивлений на некоторую функцию W(s\ подобранную таким образом, чтобы получить физически осуществимые сопротивления.

Пример 177, Преобразовать каноническую схему двухполюсника, состоящего из LC-элементов, в каноническую схему двухполюсника, состоящую из ЯС-элементов.

Решение. Входная проводимость £С-двухлолюсника

v /_■» _ _ . ^ао , sr ^{2 а}к Р he {Р>-^а\ Р + — ⁺ Г-

Р Р

Заменим р на <р(з) = 4s и умножим результат на n^(s) = l/4s:

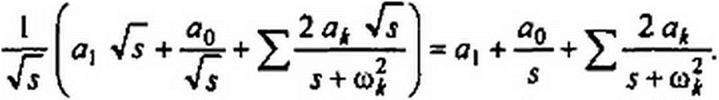В результате получили входное сопротивление канонической схемы двухполюсника, состоящего из ЯС-элементов. Следовательно,

vs

Аналогично входное сопротивление двухполюсника из /?С-элементов преобразуется во входную проводимость двухполюсника из LC-элементов: Y_lc(s)- 4s Z_K{(Vs)

В заключение отметим, что в частном случае преобразования второго рода проводят, умножая сопротивления исходной схемы на некоторую функцию не заменяя р на <р(л).

§ П6.4. Частотные преобразования цепей с распределенными параметрами. По отношению к цепям с распределенными параметрами частотные преобразования приме­няют:

1) для перехода от одного типа целей к другому (например, от £С-иепей с распреде­ленными параметрами без потерь к RC-нспям с распределенными параметрами, от LC- цепей к безындукционным flGC-цепям и т. д.);

2) для перехода от электрических цепей с распределенными параметрами к цепям с сосредоточенными параметрами.

Параметры однородной линии с распределенными параметрами на единицу длины обозначим следующим образом: Lq — индуктивность; Rq — продольное сопротивление; С_о—емкость; G_o— поперечная проводимость; /— длина линии; 0₂ и 7,— напряже­ние и ток в конце линии; й_х и Д — напряжение и ток в начале линии.

Постоянная распространения у = 7(*о ⁺ Р £) (^о + Р С_о).

Волновое сопротивление Z, = 7(*о + Р ^о)/(^со + Р Со)-

Запишем уравнение линии в Я-форме:

U \ — A О2 + В ;

/, =cu₂ + d/₂,

где X = £) = chy/; B = Z_Bshy /; D = shy//Z_e.

Систему (П6.3) представим в Z-форме, имея в виду, что Z_l( = Z₂₂ = Л/С = Z_B cth у I, Z_l2 = Z_2I = ]/C = Zjshyl. В результате получим

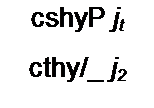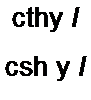Обозначим L_n = / Lq; R_n -1 R_o\ G_n = / G_o; C_n = / C_o. Тогда

(у /)² = L_n C_n p² +(£_n C„ + С_П Л„) p+ R_n G_n.

Для LC-линии без потерь (Я_о ~ G_o = 0)

Y ^LC ~ Р 7Л1 С_п ♦ -^e ~ V^o /^'o •

Для ЯС-линии (Ло = G_o - 0)

Yhie ⁼ P 7C_n *n^{; =} JRoUp Q).

Для безындукционной PGC-линии (to ⁼ 0)

Y Ir.g,c - 7^n C_n p + R_n C„ ; Z_B = 7*o/(Co ⁺ P C_o).

Линия LC без потерь переходит в ЯС-линию, а Z-матрица ДС-линии преобразуется в Z-матрицу ЯС-линии, если в Z-матрице £С-линии положить p-Js ^и умножить

сена 7*о/&•*)•

Линия с распределенными параметрами RC (L_o =G₀ =0) переходит в линию с рас­пределенными параметрами LC (Я_о ^=<^о =0). ^если в Z-матрице £С*линии положить р = ф(.$) = $^г L_n/R_n и умножить ее на s L₀/Rq.

Аналогично осуществляют переход от ДС-линии без потерь к безындукционной RGC- линяя и обратный переход, а также от /?С-линии к PGCL-линии с потерями. Различие при этих переходах только в том, какую функцию р = ф($) следует взять и каков должен быть множитель W'(s).

Определим, как путем частотных преобразований производят переход от цепей с рас­пределенными параметрами к цепям с сосредоточенными параметрами. С зтой целью рас­смотрим преобразование, которое позволит осуществить переход от безындукционной ЯС- цепи с распределенными параметрами к цепи с сосредоточенными параметрами, содер­жащими индуктивные элементы я положительные и отрицательные резисторы. Запишем выражение для Z-матрицы ЯС-цепи:

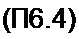| Ro~ cth yjp С„ R_n cshJ/?C_n Я_п _cshVpC_n R_n cth7pC_n R_n

Подставив

s = ch7pC„ R„ (П6.5)

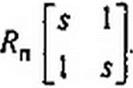и умножив полученную матрицу на W(_s) - Jp С_п R_n sh jp C_n R_n, получим Z-матрицу преобразованной цепи

Этой матрице соответствует Г-схема с сосредоточенны­ми параметрами, изображенная на рис. П6.4 (Я„ = R\

Таким образом, при частотной подстановке (П6.5} ЯС-непь с распределенными параметрами (£₀ =Gq =0) оказалась приведенной к схеме на рис. П6.4 с сосредото­ченными параметрами, которая содержит индуктивные эле­менты и положительные и отрицательные резисторы.

§ П6.5. Преобразование Брутона. Как упоминалось в § П6.1, преобразование Бруто­на состоит в том, что сопротивления всех элементов исходной схемы делят на частоту р. При этом исходная цепь с элементами Я_н, £_М,С_Н становится безындуктивной с элемен­тами С, Я. D, где D — емкостный элемент второго порядка {см. Приложение П2). Частот­ные свойства исходной и преобразованной схем одинаковы.

Преобразование Брутона проведем одновременно с нормированием и последующей денормировкой параметров схемы.

Сначала рассмотрим вопрос о нормировке параметров. Пусть элементы Я_н, £_н, С_н, £>_н некоторой исходной схемы соединены последовательно. Сопротивление исходной схемы на частоте о>

1 1

------ “ ⁺------ o------ •

Осо)²о_к

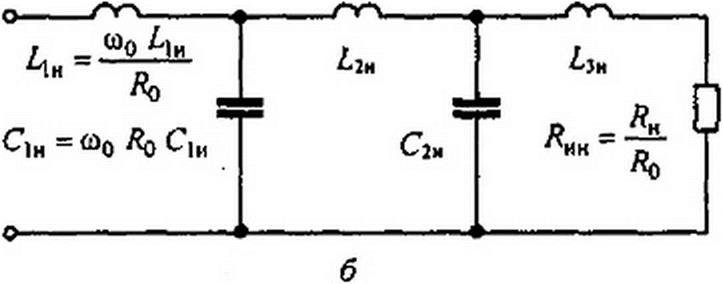
Нормируем это сопротивление no величине, поделив на некоторое сопротивление Я_о (Ом) и затем нормируем по частоте (рад/с), введя нормированную частоту х = о/о)о- Если речь идет о фильтрах, то берут равной либо частоте среза НЧ-фильтра. либо центральной частоте полосы пропускания ПП-фнльтра.

Индексом «к» будем обозначать нормированные по величине и по частоте значения величин. Нормированное сопротивление схемы в безразмерных единицах:

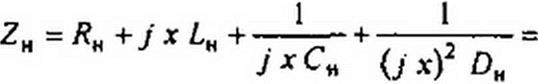R» ₊ J * ^L » ₊ । ₊ 1

Яо Я_о jx <о₀ С_и Я_о (j _х)² R_o 1)_ц '

Почленно сопоставляя, находим связи между нормированными и ненормированными величинами:

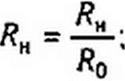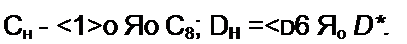Рис. П6.5

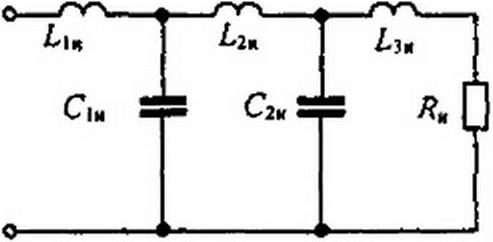
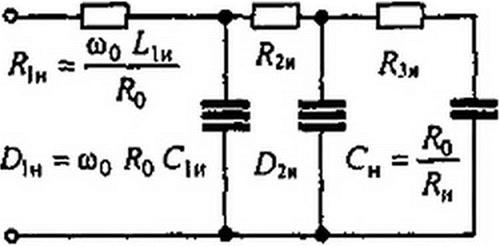
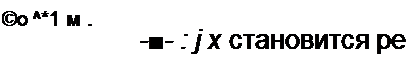В качестве исходной схемы, к которой применим преобразование Брутона, возьмем схему на рис. П6.5, а. От нее сначала перейдем к схеме с нормированными параметрами с нулевой размерностью (рис. П6.5, б). Последнюю схему преобразуем по Брутону, поде­лив сопротивление каждого элемента на р = j х. При этом все продольные индуктивные

элементы перейдут в резистивные. Так, сопротивление j х

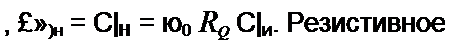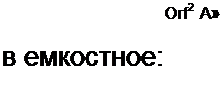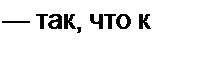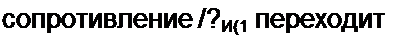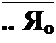, R»

С_н ⁼Яо/Я_н. Схема, преобразованная по Брутону, с нормированными безразмерными параметрами изображена на рис. П6.5, в. Используя формулы (П6.6), осуществим денормировку. Окончательная схема с денормированными параметрами изображена на рис. П6.5, г. Параметры ее зависят от ©о и параметров исходной схемы.

В схеме на рис. П6.5, г два емкостных элемента второго порядка —D_t и D₂. Каж-¹ дый из них реализуем схемой рис. 4,11, а. В каждой из этих схем полагаем Z\ = Zy = —!—, Z₂ - Z₄ = R, а сопротивление Z₅ берем резистивным и различным. При

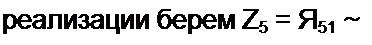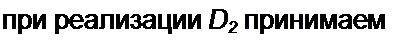Z₅ = R_i2 =---------- Числовые значения R и С_А берем такими, чтобы была обеспечена нормальная работа операционных усилителей в схемах на рис. 4.i I, а.

В заключение обратим внимание на то, что нормирование параметров в § П6.5 выполнено несколько иначе, чем это принято в литературе по электрическим фильтрам и описано в § 10.11. Отличие в том, что в § П6.5 Я_о (Ом), ©₀ (рад/с), тогда как обычно в литературе по фильтрам и в § 10.10 (при нормировке) полагают, что Л_о и ©о имеют ну­левую размерность. В § П6.5 в нормированной схеме на рис. П6.5, б параметры имеют нулевую размерность, тогда как в нормированных схемах, когда Rq и ©о приняты без­размерными, L_H (Гн), С_н (Ф), Л_н (Ом). Сделано это для того, чтобы при преобразова­нии схемы по Брутону при переходе от рис. П6.5, б к рис. П6.5, в все элементы схемы на рис. П6.5, в, как и схемы на рис. П6.5, б, имели нулевую размерность и чтобы после денормировки элементы окончательной схемы на рис. П6.5, г имели естественную размер­ность, т. е. чтобы все R (Ом), D (А-с²/В) и С (Ф).

Приложение П7