Случайные процессы в электрических цепях

Дата: 2025-06-02; Просмотры: 14

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

§ П4.1. Случайные процессы. Корреляционные функции. Положим, что есть несколько систем, находящихся в одинаковых условиях, и в них происходят в принципе одинаковые процессы. В силу влияния различных случайных факторов, имеющих вероят­ностный характер, процессы в системах могут несколько отличаться друг от друга. В результате наблюдения можно установить, какая величина при фиксированном моменте времени / является наиболее вероятной.

Плотность вероятности случайного процесса W(x, t) выражает вероятность того, что в момент времени t значение величины х находится в интервале от х до x + dx.

Функцией распределения F(x) называют вероятность наступления события, при котором значение величины х, характеризующей это событие, находится в интервале от -оо до х.

Случайные процессы могут быть разделены на стационарные и нестационарные. Ста­ционарными называют случайные процессы, для которых все функции распределения не зависят от изменения начала отсчета времени. Для нестационарных случайных процес­сов функции распределения зависят от времени.

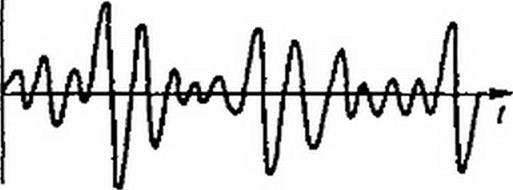
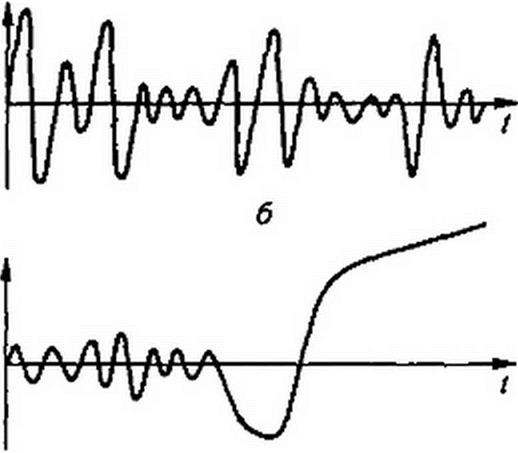
В качестве примера на рис. П4.], а, б изображены кривые некоторого стационарного случайного процесса. Для этих кривых вероятность возникновения колебания с некото­рой амплитудой останется той же, если сдвинуть начало отсчета времени. Иная картина имеет место на рис. П4.1, в, г, изображающих кривые х(/) для некоторого нестационарно­го случайного процесса. На рис. П4.1, в начиная с некоторого момента времени x(t) нео­граниченно возрастает, а на рис. Г14.1, г — стремится к нулю. Следовательно, для этих кривых сдвиг начала отсчета времени изменяет вероятностные зависимости.

Для стационарных случайных процессов среднее по множеству х равно среднему по времени (х), те. х = (х). Это положение называют эргодической теоремой (гипотезой). Эргодическая теорема позволяет, обрабатывая одну из временных зависимостей х(г), по­лученную экспериментально, судить о статистических свойствах всех зависимостей х(/) при стационарном случайном процессе в изучаемой системе.

Для характеристики случайных процессов х(г) вводят автокорреляционную и взаим­ную корреляционную функции.

Автокорреляционная функция К(т) является мерой взаимной связи функции х(0 и функ­ции x(t - т), смещенной по отношению к х(/) на время т:

, т

lim ——■ |х(/)х(г-x)di. (П4.1)

² ' -Г

Свойства /?(т):

1) Я(т) — функция четная, т. е. Л(-т) = R(x\ в этом можно убедиться, введя в (П4.1) новую переменную = / + т;

2) если х(/) — функция периодическая, то для нее /?(т) может быть представлена в виде суммы автокорреляционных функций от постоянной и синусоидально изменяющихся со­ставляющих;

3) если в х(г) имеются гармонические составляющие, то К(г) не содержит информа* ции о начальных фазах гармонических составляющих;

4) для х(/) без постоянной и гармонических составляющих Л(т) максимальна при т “ 0;

5) для случайных функций времени без постоянной и гармонических составляющих Я(т) уменьшается с увеличением т и уже при сравнительно небольших т стремится к нулю (объясняется это тем. что для чисто случайного процесса значение х(г~т) уже при отно­сительно небольшом х не зависит от того значения, которое имела эта функция х(/) в момент времени г).

Взаимной корреляционной функцией Двух функций времени х(г) и у(г) называют функцию, определяемую следующим образом:

, г

Яо«(О= [х(/)х(/-т)а/. (П4.2)

/ 2 / *

Функция /?^(т) является мерой взаимной связи двух случайных функций времени.

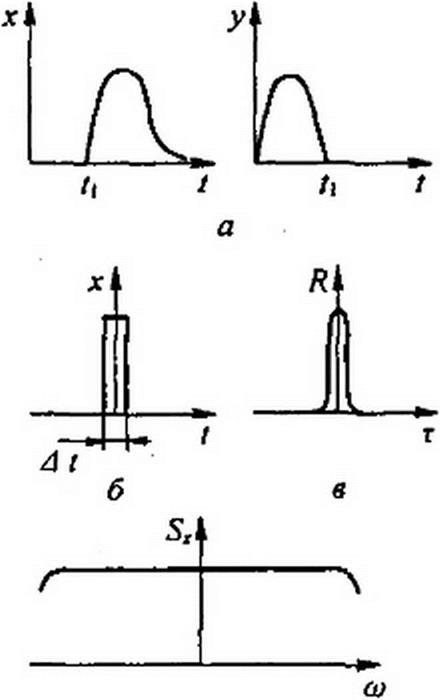
На рис. П4.2, а изображены две произвольные функции времени х(/) и y(t), которые позволяют наглядно пояснить свойства функции ^(т).

1. Функция Я (г) зависит от того, сдвинута функция y(j) на +т или на -т, т. е. Я^Д-т)* R-_X>.(x). Если кривую y(t) на рис. П4.2, а сдвинуть на +т влево, т. е. взять функцию Х^{/ + т})> то произведение х(/)Х^{/ + т}) будет равно нулю для любого I, следова­тельно, и Если же эту кривую сдвинуть на -т вправо, т. е. взять функцию

y(t -т), то на некотором интервале времени произведение ординат кривых х(Г) и y(i~ т) не будет равно нулю.

2. Сдвиг функции ХО влево на т дает тот же результат, что и сдвиг функции х(1) на -т вправо. Поэтому /?,у(т)= ^(-т).

3. Для случайных функций времени х(/) иу(г), не содержащих постоянной и гармони­ческих составляющих одинаковой частоты (для некоррелированных функций), R_xy (x) = Q.

Рис. П4.2

§ П4.2. Прямое и обратное преобразования Фурье для случайных функций времени, К случайным функциям времени и их корреляционным функциям применяют преобразование Фурье. Так как в общем случае случайная функция времени x(t) или ее корреляционная функция может и не стремиться к нулю при / -> ±«, то, для того чтобы к ним можно было применить преобразование Фурье, поступают следующим образом: преобразование Фурье применяют к функция х, (г), которая не равна нулю в интервале от -Т до ч-T и равна нулю вне этого интервала. Если затем 7*->а>, то x_t(/) будет стремиться к х(6, а Фурье-изображение функции х,(/) — к Фурье-изображению функ­ции х(г).

Подобное рассуждение может быть проведено и по отношению к Фурье-изображению корреляционной функции.

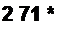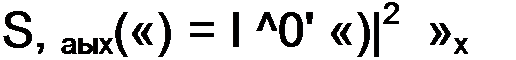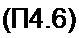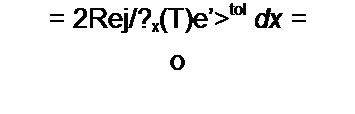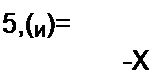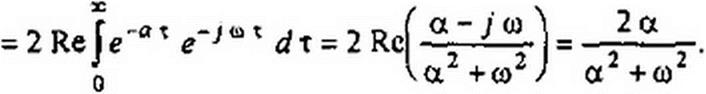На рис. П4.2, г качественно построен график 5_Х(«) для случая, когда а очень вели­ко. Если а очень велико, то влияние иг на значение знаменателя S_x(w) сказывается только при очень больших w, соизмеримых с а, т. е. спектральная плотность мощности 5_х(а>) кратковременного импульса в очень широком диапазоне частот постоянна. Таким обра­зом, чем уже импульс (чем он короче во времени), тем шире его частотный спектр.

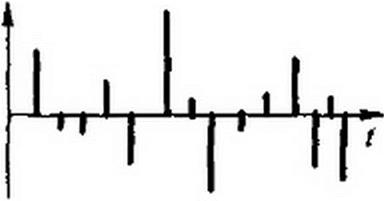
Белый шум представляет собой совокупность множества беспорядочно (без всякой связи) следующих друг за другом игольчатых импульсов (рис. П4.2, д), амплитуды кото­рых имеют случайный характер и подчиняются закону нормального распределения веро­ятности. При этом плотность распределения вероятности

(*-а)

W(x) = —!==■ е ' °² ,
ст у2 п

где а— математическое ожидание; ст² — дисперсия.

Так как спектральная плотность каждого импульса постоянна в достаточно широком

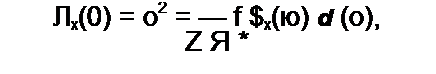диапазоне частот, то и для белого шума (о) = const. Если в формуле (П4.5) положить t = Q и учесть, что Я_х(0) равно дисперсии о², то т. е. дисперсия равна средней мощности флюктуации стационарного случайного процесса.

§ П4,4, Источники внутренних шумов в электрических цепях. Резисторы, элект­ронные лампы, транзисторы, магнитные усилители и многие другие элементы схем яв­ляются источниками внутренних шумов. ЭДС, которые при расчете эквивалентны этим шумам, обычно очень малы и составляют часто несколько микровольт. Если шумящие эле­менты схем включены на входе усилителя, имеющего очень большой коэффициент усиле­ния, то шумы ограничивают порог чувствительности схемы и их приходится учитывать.

Резисторы как источник шума. Вследствие хаотического теплового движения элект­ронов в некоторый момент времени на одном конце резистора образуется избыток элект­ронов, а на другом конце — недостаток. В смежный момент времени может возникнуть обратная картина. На концах резистора как бы возникает некоторая ЭДС.

Шум, возникающий в резисторе R (Ом), является белым шумом и имеет спектраль­ную плотность 5_ш(о)= 2 k Т R, где А=1,3в-1О“²’ Дж/град—постоянная Больцмана; Т — абсолютная температура резистора.

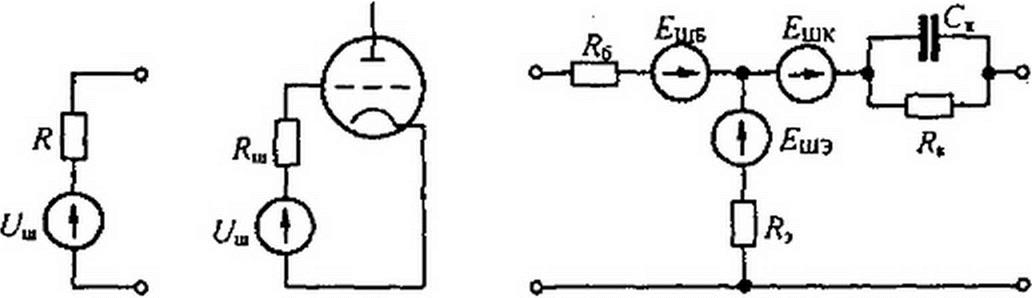
Шумящее сопротивление при расчете эквивалентно схеме рис. П4.3. а. В ней после­довательно соединены нешумяшее сопротивление и источник ЭДС. Квадрат напряжения этого источника

I/² = 5_ш(ф) Дц/л - 4 к Т R

где Део = 2 л Д/ — полоса пропускания усилителя, на вход которого включено шумящее сопротивление.

Рис. П4.3

Дробовой эффект в электронной лампе. Эффект испускания электронов нитью нака­ла лампы носит случайный характер. В некоторый момент времени из нити накала выле­тает больше электронов, а в смежный с ним момент времени — меньше. В результате анодный ток при отсутствии сигнала на сетке лампы непостоянен и имеет некоторую пе­ременную составляющую, которая колеблется около среднего значения анодного тока.

Эффект называют дробовым, так как он напоминает шум дробинок при их ударе о мишень. Шум, вызванный дробовым эффектом, является белым шумом, спектральная плот­ность которого не зависит от частоты. При расчете дробовой эффект учитывают, включив в сеточную цепь лампы рис. П4.3, б резистор R = Я_ш и источник ЭДС с напряжением С/_ш, (У², = 4 к Т R Д/.

2^з

Для маломощных триодов пользуются формулой =--- (кОм), где S — крутизна

характеристики лампы, мА/B. Для многосеточных ламп значительно больше, чем для триодов.

В транзисторах шумы возникают вследствие дробового, диффузионного и фликкер- процессов. Все их сводят к тепловому шуму. В качестве примера на рис. П4.3. в изобра­

жена шумовая схема биполярного транзистора, включенного по схеме с общей базой (срав­ни со схемой рис. 15.24, б).

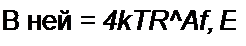l_n=4kTR_tAf, £щ_К = 4 £ Г |ZjJ Д/. Влияние шумов на

выходную величину оценивают отношением квадрата действующего значения напряжения сигнала к среднему квадрату напряжения шума (дисперсии) на выходе устройства. Когда нелинейная схема работает в режиме, близком к линейному, и & ней может быть выделен доминантный источник белого шума, то принимают, что спектральная плотность шума ^_ш(0) = 4£ Т R. Комплексным методом подсчитывают передаточную функцию четырех­полюсника от шумовой ЭДС на выход четырехполюсника К (J со), яо формуле (П4.6) оп­ределяют спектральную плотность напряжения шума и, интегрируя ее по частоте ОО

вых (о) (К О' ш)|² d f, подсчитывают среднее значение квадрагта шумового напря-

о

жения на выходе четырехполюсника. Затем определяют отношение сигнала к шуму.

Приложение П5

Дискретные сигналы и их обработка

§ П5.1. Теорема Котельникова. Положим, что некоторый аналоговый сигнал х(г) — если его мысленно лериодизировать во времени (см. § 9.7, рис. 9.4, а) — содержит гар­моники в диапазоне частот 0 -f_m. Каждая гармоника ряда Фурье, в который мог бы быть разложен периодизированный аналоговый сигнал, характеризовалась бы двумя величина­ми — амплитудой и фазой. Поэтому для отображения в дискретизированном сигнале всех частот аналогового сигнала надо при дискретизации взять 2/_т отсчетов’’.

Если время отсчета обозначить Г, интервал между отсчетами △, число отсчетов N, то

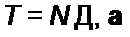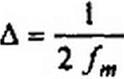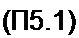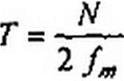
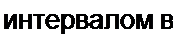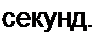(П5.2)

Соотношение (П5.1) выражает собой содержание теоремы В.А. Котельникова, сфор­мулированной им в 1933 г.: любую функцию времени, содержащую гармоники в диапазо­не частот 0-/„, можно передавать с помощью чисел, следующих друг за другом с

§ П5.2. Частотный спектр дискретизированного сигнала. Будем уменьшать шири­ну каждого импульса, сохраняя его площадь. Тогда дискретизированный сигнал рис. 9.4 можно представить в виде суммы произведений двух функций

X

*_л0) = £т(л Д) 2(/ - и Д). (П5.3)

Положим, что аналоговый сигнал x(j) имеет частотный спектр X{j со). Периодическую

•X

функцию из единичных импульсов (рис. П7.1, в) Ь({)= £$(/-« А) разложим в ряд

Лх-Х

X 2л// _х
i(/)=£Qe' а ₌

где со_р = 2 л/Д — частота дискретизации. Коэффициенты этого ряда

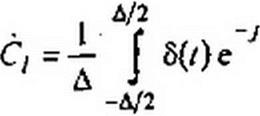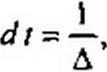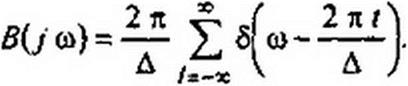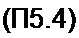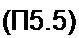
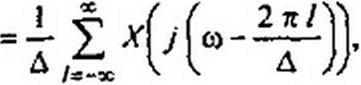В соответствии с тем, что х_д(/)— это произведение двух временных функций, спектр дискретизированного сигнала X_a(j со) определим через свертку спектральных плотнос­тей этих функций:

2 п ^J 2 л ^J Д \ Д 7

-х -х

‘‘На периоде высшей гармоники 1//_т должно быть взято по крайней мере два отсче­та, иначе не будет учтено влияние высшей гармоники на величину отсчета. Полагаем, что с увеличением номера высшей гармоники амплитуда ее уменьшается.

т. е. X_n{j со) представляет собой поделенную на д сумму частотных спектров исходного сигнала х(/), сдвинутых по оси частот на интервалы &_р = 2 л/Л, равные угловой часто­те, с которой следуют импульсы дискретизации.

Для того чтобы периодическое повторение спектра, вызванное периодизацией во вре­мени, не изменяло повторяемый спектр, необходимо и достаточно выполнение неравен­ства (Ор где со„— наивысшая частота в спектре сигнала x(t). Обычно берут

^W_P - (2-5) 2 <d_OT. после чего определяют Д = 2л/(1)_р.

§ П5.3. Дискретизация частотного спект ра. Пусть сигнал имеет длительность Т_с и частотный спектр 5_с(у ш). Дискретизируем спектр S_c(j to) с интервалами дискретизации 2

по частоте =■—. По аналогии с предыдушим 5_д(усо) запишем так;

^д(у®)= f SQ aqJ5(o)-AQJ = SO») X (П5.6)

А=-х

Временной сигнал, соответствующий 5_Д(/ со).

= Е 50^_д)б(а)-АП_д) = 5С/©) f 3(ш-ЛП_д) (П5.7) Jtc-x X

Функцию Е ) разложим в ряд Фурье

X 5((0~*П_я) = X^c^7rw7<- (П5.8)

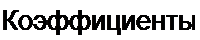l-~cc

C_r=-E f J- (П5.9)

¹² д ^О_д/2 ^ПД

x

^,n5J0 >

т. e. дискретизированному с частотой Q_n частотному спектру во временной области соответствует периодический сигнал с периодом Т_с. Если на интервале 0-Г_с сделано ., . 7*_с 2 л 2 л

N отсчетов, то Д = — =----------- =----------- .

* о>^ N Я_д

На выбор П_д жестких условий, подобно наложенным на Д, не вводят.

§ П5.4. Прямое преобразование Фурье дискретизированного сигналя. На интер- A^f*“l

вале 0 - Т_с x_a(t) = £х(^п Д) 6(f - п Д) может быть представлен комплексным рядом Фурье л=0

(предполагается, что этот массив значений повторяется бесконечное число раз с перио­дом Т_с = N Д):

*

*_д(0= ^г' . (П5.П)

Здесь

С*=~/*_д(г)е ^7< di.

о

Введя безразмерную переменную а = </Д и обозначив х(пЛ) = х(л), получим

I \AX-I J N N-i ■

G =77— f ^х(п)5({а - п)с АГ d(Aa) = --f X^)S(a-«)e ^А da.

о /«о M о >^о

Учитывая фильтрующее свойство 5-функции, имеем

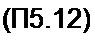, N~\ t^2Kkn

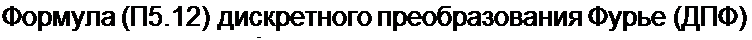" «=o

00

мулы Sljo)- j/(0e"-'“' dt для непрерывных сигналов.

-oo

Свойства коэффициентов С_к:

1 лм

О Со =77

2) С_к = С_{к ± а N}, где а — целое число;

1 лм

4) если отсчетные значения х(п) вещественные, то

Л,.! _w _t 2п»к

Q-*=77Z^xW« ⁿ =77^^х("^{)е N =Ct}' Ш5.13) ^Л >1=0 ^л п=0

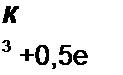В качестве примера определим коэффициенты ДПФ сигнала х_д(/) на интервале 0 - Т_с, заданного шестью дискретными значениями (0,5; I; 0,5; 0; 0; 0). Имеем

С_о = — (0,5 +1+ 0,5) = —; С_{=- 0,5 + I е о 3 о

Если применить прямое преобразование Фурье к дискретизированному сигналу х_д(/) и затем провести дискретизацию спектра по частоте с интервалом О_я, то для ДПФ по­лучим

• J - j — п к

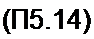ЭД=£ф)е " (Л «0.1.2,...Л-1) „=о

Через S_k обозначено 5(А'О_д), а через х(п) -> Д) (П5.14) отличается от (П5.12) множителем 1//V, поэтому C_k=S_k/N.

Для определения выборочных значений спектра $_С(Л£2_Д) надо S_k, вычисленные по (П5.14), умножить на величину дискретизации по времени Д в соответствии с (П5.5).

. 2 я

Дискретную функцию е ^N принято обозначгпъ W. Тогда

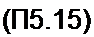лм £х(п)^"*(А=0, 1,2.......................... N-1).

»=о

В научно-технической литературе не принято ставить точки над 5(A) и х(л), хотя эти величины в общем случае комплексные.

§ П5.5. Определение непрерывного сигнала x(t) по коэффициентам ДПФ. Вслед- 2 ж f

ствие периодичности коэффициентов С_к, а также функции е ^N по индексу к с пе­риодом /V выражение (П5.11) можно записать так:

N-1 . j ^*.1

^Те . (П5.16)

*=0

*

Так как C_N__K = С\, то

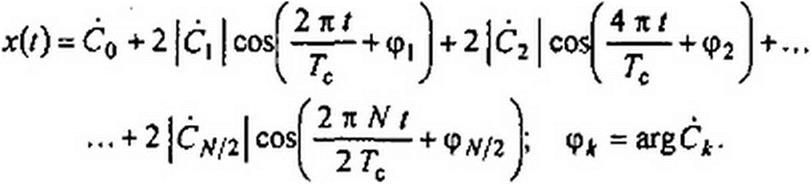Для примера § П5.4:

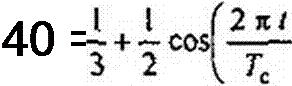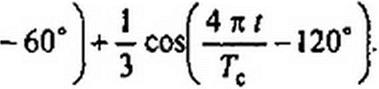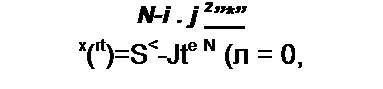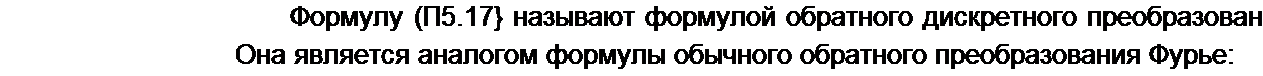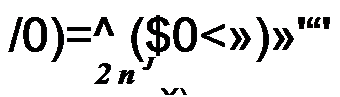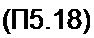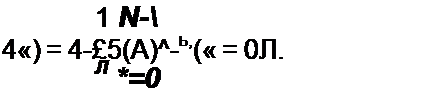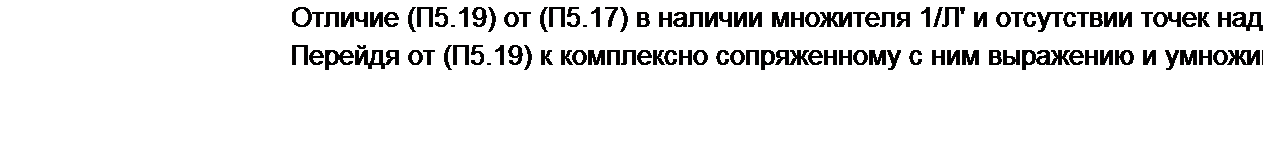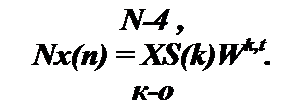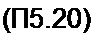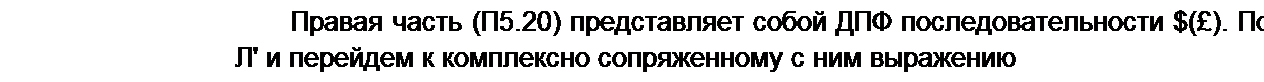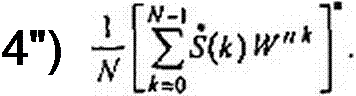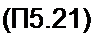Из формулы (П5.21) следует, что х(м) или ОДПФ можно вычислить по тому же алго­ритму, что и ДПФ.

§ П5.7. Вычисление дискретного преобразование Фурье. Быстрое преобразова­ние Фурье. Если вычисление проводить по формуле (Д.13), то надо произвести Л/² ум­ножений и jV(jV-I) сложений комплексных чисел, а всего Л/² + Л^(Л1-|) операций. С целью уменьшения числа операций разработаны алгоритмы быстрого преобразования Фурье (БПФ). В основу их положено разложение N точечного ДПФ на набор ДПФ мень-

шего порядка за счет использования следующих свойств дискретной экспоненты .2 к

W*" =е^{-/ N} •

1. Свойство симметрии W^^N~ⁿ^ = J .

2. Свойство периодичности = И^*^+Л/)и.

3. Wu =W_N> так как е ^{1 N} =е .

4. И^²=-1, так как е ^{N 2} = е'-^/*=-1.

Алгоритмы БПФ, основанные на разложении временной последовательности х(л) на уменьшающееся число подпоследовательностей, называют алгоритмами БПФ с прорежи­ванием по времени. Если N целая степень числа 2, т. е. N = 2^V, то число умножений ком- N

плексных чисел равно — log₂ N, а число сложений — N log₂ N.

Алгоритмы БПФ, в которых на уменьшающиеся последовательности разлагается последовательность коэффициентов S(k) дискретного преобразования Фурье, называют алгоритмами БПФ с прореживанием по частоте.

§ П5.8. Дискретная свертка во временной и частотной областях. Запишем интег­рал Дюамеля (формулу свертки):

I

*вых (^т) = f ^Х»Х (^т)0 - т) т, (П5.22)

о

где х_вх(з), х_ВЬ1Х(т)— входной и выходной сигналы; Л^б(г)— импульсная переходная характеристика четырехполюсника. При цифровой обработке сигналов вместо обычной свертки используют дискретную. С этой целью разобьем интервал времени 0-Т_с на Д' одинаковых интервалов длительностью Д, текущее значение интервала п Д обозначим п (О,L2,У-!), дискретизированные значения х_вых(г) обозначим х_8ЫХЛ,, ^Х»х (^х) ^Хвх»• В свою очередь

Л⁵ (/- т)4 (т = О,I,...,/V-1).

Дискретную свертку записывают аналогично свертке обычной

АМ 5

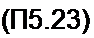ВЫХ m ⁼ У. -^вх w ^m-ir

Для приведения в соответствие с формулой (П5.22) надо выполнить условие А⁵ (?и) - й⁶ (л) Д. где h^b{m)—безразмерная импульсная характеристика. Дискретную свер­тку по (П5.23) называют линейной, если х_вхм и — нулевые вне интервалов их оп­ределения, т. е. не являются периодическими. Если х_ВХ(, и й® имеют соответственно /V, и отсчетов, то при линейной свертке х_8ЫХт имеет длину в + N₂ -1 отсчетов. Свер­тку по (П5.23) называют прямой. Она требует N_{ умножений. Дискретную свертку в частотной области вычисляют с помощью алгоритма БПФ и называют ее быстрой или вы­сокоскоростной. С этой целью текущие значения х_вх „ и выражают в виде ОДПФ от спектров соответствующих функций:

Тогда

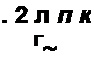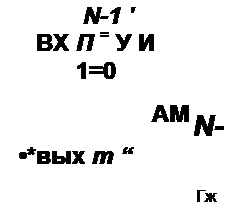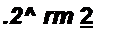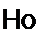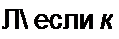Поэтому

. (П5.24)

i=O

Формула (П5.24) означает, что х_выкт есть ОДПФ от произведения C_XBXJt С_ьл N. В ней учтено, что г = к, и потому взята одна сумма, а не две (суммировать дважды пб од­ному индексу не имеет смысла).

С использованием предыдущих обозначений запишем х_|ыхт в виде:

ЛМ i **»>*

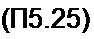
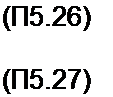УС »е *
вых к ^с

Следовательно,

Схаых* ~^хвхк

*$вых к ~ $х вх к ■

Таким образом, коэффициенты ДПФ свертки являются произведениями коэффициен­тов ДПФ свертываемых функций. Поэтому для вычисления свертки двух последователь­ностей надо вначале найти их ДПФ, перемножить коэффициенты, а затем применить ОДПФ. Причем для вычисления ДПФ и ОДПФ можно использовать алгоритм БПФ. Од­нако в этом случае свертка получается циклической или круговой (периодической), а саму процедуру называют теоремой о круговой свертке ДПФ.

При использовании ДПФ и ОДПФ дискретизация во временной области приводит к тому, что спектр выходного сигнала становится периодическим, а при дискретизации а частотной области периодическим становится сам выходной сигнал с периодом, равным числу выборок. Для того чтобы с помощью периодической свертки можно было вычис­лять линейную, необходимо период круговой свертки сделать равным L = 2^V 2 (yVj + /V₂ “• О отсчетам. Для этого последовательности х»_х?( и (длиной и N₂) дополняют до длины L необходимым числом нулевых отсчетов. Затем находят L то­чечные ДПФ дополненных последовательностей, перемножают их и выполняют ОДПФ произведения.

Для осуществления быстрой свертки необходимо вычислить два БПФ для L точек и

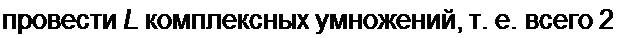f — log₂ L !+ L комплексных умножений

\ 2 j

или 4 L (log₂ £ + I) действительных умножений. Быстрая свертка эффективнее прямой при

Приложение П6