Исследование процессов в неэлектрических системах на электрических моделях-аналогах
Исследование процессов в неэлектрических системах (механических, акустических, тепловых, гидравлических и др.) или в частично неэлектрических (например, в электромеханических) часто производят на электрических моделях-аналогах.
Стремление использовать для этой цели электрические модели объясняется тем, что:
1) электрические параметры можно легко изменять в широких пределах;
2) токи и напряжения можно измерять с большой точностью;
3) токи и напряжения относительно просто записать на осциллографе.
В качестве неэлектрических будем рассматривать механические системы.
Механические системы подразделяют на системы поступательного, вращательного и поступательно-вращательного движения. В каждой из этих систем могут быть активные и пассивные элементы.
Активными являются источники силы /, источники скорости v для систем поступательного движения, а также источники вращающего момента М и угловой скорости со для систем вращательного движения.
Пассивными являются элементы упругости, трения и массы. Как и при рассмотрении электрических цепей, эти элементы часто идеализируют, например считают, что идеальная пружина обладает только упругостью и не имеет массы.
Для заданной механической системы сначала составляют схему замещения, а затем, используя аналогию между механическими и электрическими величинами (рассмотрена далее), образуют электрическую схему-аналог, которую и подвергают исследованию (экспериментальному или теоретическому).
Перед составлением схемы замещения механической системы необходимо:
1) выбрать систему отсчета для сил и скоростей (соответственно для вращающих моментов и угловых скоростей);
2) соединить между собой узлы, имеющие одинаковую скорость или одинаковое смещение;
3) соединить неподвижные узлы в один узел;
4) на схеме замещения между соответствующими узлами изобразить активные и пассивные элементы, имеющиеся в изучаемой системе.
Пример 177, Механическая система рис. П3.1, а образована телом массой т, опираю- щимся на пружину упругости 5 (5= I /е, где е — податливость). На тело действует внешняя силаД/), являющаяся функцией времени /. При движении тела в вертикальном направлении возникает вязкое трение о среду. Сила вязкого трения пропорциональна скорости v перемещения тела. В схеме два узла: подвижный а и неподвижный Ь.
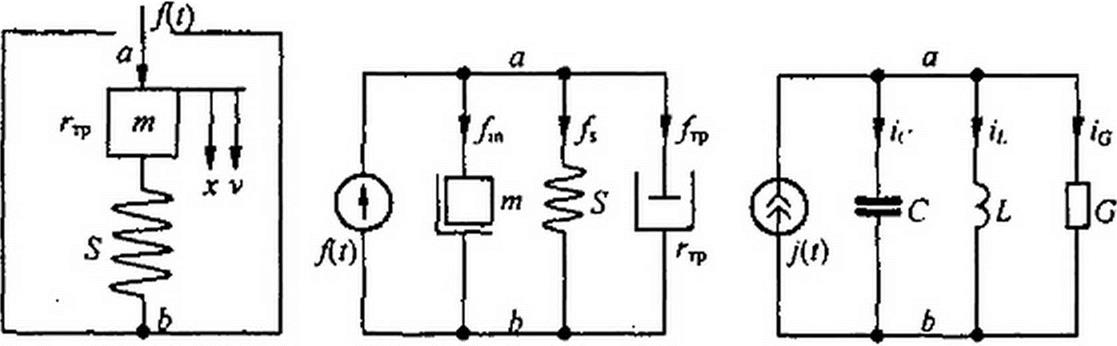
a б в
Рис. ПЗ. 1
Решение. Выберем положительное направление для отсчета перемещения телах, считая за исходное положение тела при отсутствии силыДг). Положительное направление для скорости v показано на рис. П3.1, а. В схеме на рис. ПЗ. 1, б четыре ветви. В первой включен источник силы Д/), во второй — масса т, в третьей — идеальная пружина упругости s, в четвертой — сопротивление трения
Для схемы на рис. П3.1, б составим уравнение по первому закону механики. Согласно этому закону, сумма всех внешних сил, действующих в некотором узле, должна быть равна сумме сил реакций в этом же узле. В узле а действуют три силы реакции: jm -т-—-— реакция системы, обусловленная силой инерции; fs =— vrfr— реакция dt е J
системы, обусловленная деформацией пружины; ~ гтр v— реакция системы, обусловленная трением.
По первому закону механики,
dv 1 ; . ,, ,
т—~ + - Ivdt + r v = f(t) die* p или
fm + fs + ftp ~ /V)-
Между отдельными элементами механической системы и элементами соответствующей ей электрической модели (системы) может быть аналогия двух типов, поскольку для каждой электрической цепи может быть составлена дуальная ей цепь.
При аналогии первого типа сопоставимыми величинами являются сила f— напряжение и, скорость v — ток I, масса т — индуктивность L, податливость пружины е — емкость С, сопротивление трения — электрическое сопротивление /?.
При аналогии второго типа сопоставимыми величинами являются сила f — ток /, скорость v — напряжение и, масса т — емкость С, податливость е — индуктивность L, сопротивление — электрическая проводимость G.
На рис. П3.1, в изображена электрическая схема, соответствующая схеме замещения механической системы рис. П3.1, а по аналогии второго типа. Для нее
_ du 1 r , _ . ,
или C — + — iudt + Gu = j(t\ dt L J
где и — напряжение между узлами а и Ь.
Характер изменения напряжения и во времени в схеме рис. П3.1, в аналогичен характеру изменения скорости v в системе рис. П3.1, д. если параметры электрической схемы подобраны соответствующим образом.
Приложение П4








