§ ГН.9. Сопоставление направленных и ненаправленных графов.

Дата: 2025-06-02; Просмотры: 14

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

1. В направленных и ненаправленных графах расчет состоит из простых и наглядных операций, при проведении которых мала вероятность ошибки.

2. По сравнению с обычными алгебраическими методами решение системы уравне­ний с помощью графов может дать некоторую экономию времени.

3. При составлении определителя системы ненаправленного графа отпадает необходи­мость подсчитывать взаимно уничтожающие друг друга слагаемые, которые появляются при раскрытии определителя матрицы проводимостей системы уравнений, составленных по методу узловых потенциалов.

в — простота нахождения передачи по (П 1.1).

Однако, поскольку граф в готовом виде не задан, сначала нужно построить граф и под­считать передачи его ветвей.

5. Преимущество ненаправленных графов состоит в том, что не требуется составлять никаких уравнений и строить граф (так как графом является сама электрическая схема). Однако определение передачи по (Г11.3) требует несколько большего времени, чем под­счет по (П 1.1).

Приложение П2

Имитированные элементы электрических цепей

В автоматике, связи, информатике, радиоэлектронике все большее применение нахо­дят электрические схемы, выполняющие функции отрицательных резисторов, отрицатель­ных емкостей, заземленных и незаземленных имитированных индуктивных элементов без потерь и с потерями, частотно—зависимых индуктивных и емкостных элементов второго порядка (ЧЗОС), а также высокоомных резистивных элементов, имитированных переклю­чаемыми конденсаторами. Реализуют эти элементы (работающие на относительно малых токах) обычно с помощью схем с ОУ. Рассмотрим, как их можно осуществить.

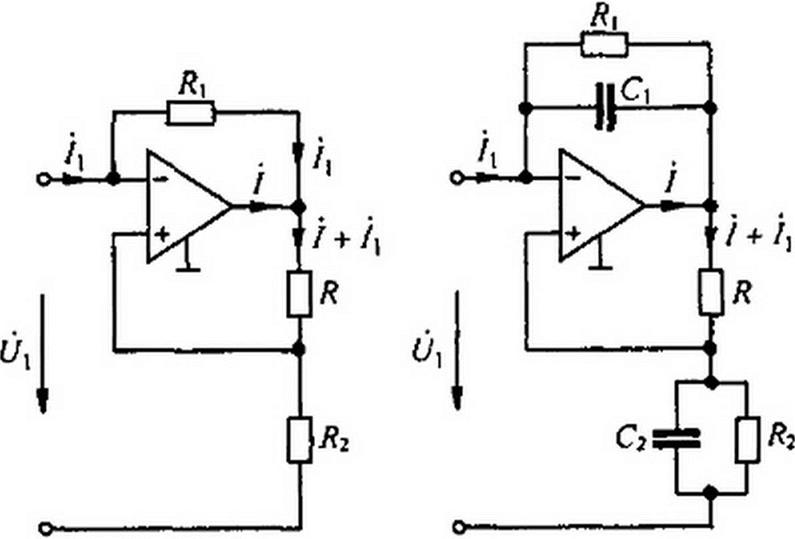
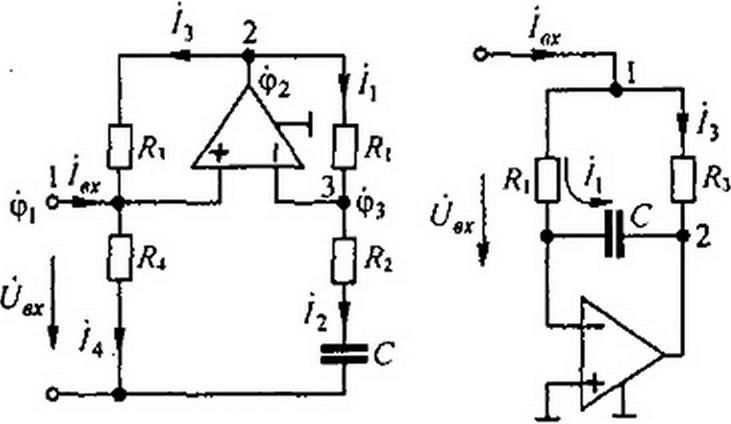
а) 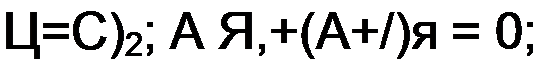Реализация отрицательного резистивного элемента с помощью конвертора отрица­тельного сопротивления (рис. П2.1, а}. В этой схеме

/j -Ь / - ^2 ~ Л ^2 ^и ” А ^вх ” ^2 ^2*

Следовательно,

/, Л,=-(/_|+/,)я=-/₂Я; А =-^ Входное сопротивление

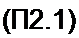U ] /₂ Я₂ _ Я) Я₂

•^х= А ⁼-/₂я/я,я ’

б) Реализация отрицательного емкостного элемента. Схема реализации представлена на рис. П2.1, б. Она отличается от схемы рис. П2.1, а тем, что параллельно резистору R_} подключен конденсатор емкостью С_ь а параллельно резистору Я₂ — конденсатор емко­стью С₂. Обозначим

Рис. П2.1

а б

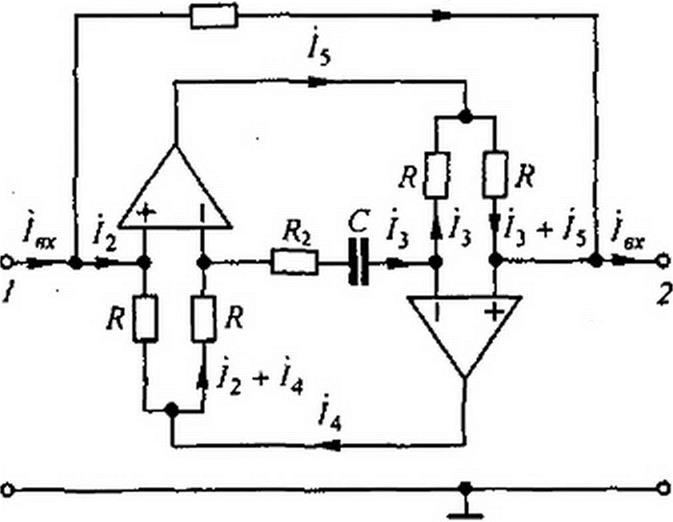
Рис. П2.2

В соответствии с формулой (П2.1) входная проводимость схемы

= --4- = -4- «I - Я, Я₂ С, С_г е>²) * j а (Я, С, <■ Я₂ С₂))..

Z] Z₂ Л) «2

Схема имитирует отрицательную емкость C_ltM = - — Q + — С₂ 1 при частоте (1>о = 1 /%/ /?| С| Я₂ С2 •

в) Реализация заземленного индуктивного элемента без потерь.

Реализация осуществляется с помощью схемы рис. 4.11, а. Для этой схемы в §4.14

III

была выведена формула для входного сопротивления Z =—1—-—Если принять

j ^Z 2 ^Zt

Z₄ = —------ . a Z₍ = Z₂ - Z₃ - Z₅ = Я, to Z_BX = j w C R². ^т- ^e- заземленная имитированная индуктивность £_)|и = с R².

г) Реализация заземленного индуктивного элемента с потерями.

Проше всего реализация осуществляется с помощью схем на рис. П2.2, а, б. В каждой из схем используется по одному ОУ. При выводе формул будем пользоваться обозначениями

токов и потенциалов, указанных на этих схемах. Для схемы на рис. П2.2, а: /₄ =

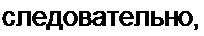, Фз-Р., / *12%.. / /, я. =./,

³ /?3 ¹ /?, ² 1 + ;о/?₂с 113 3

; . 7<оЛ,С . . . ф,

^{, = Vl} w.jaKiCY ^{Входаой так} -'1 -т;-

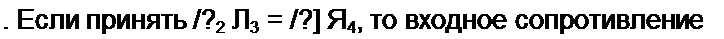_ Ry + (R₂ Ry - R] R«)j(»C ¹ R_y R< (1 + j<oR₂ C)

Таким образом, при условии Л₂ Ry = R\ R* схема реализует индуктивный элемент £_нм =Ri R₄C и последовательно соединенный с ним резистор R₄. Проведем выкладки для схемы рис. П2.2, б. Так как напряжение на входе ОУ стремится к нулю, то = (J_W{R_X. Из условия равенства падения напряжения между узлами / и 2 по двум параллельным

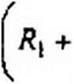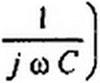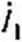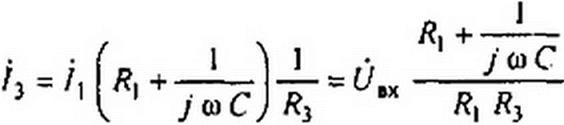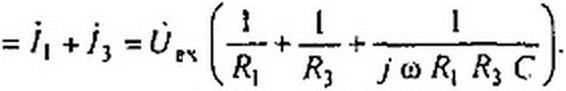111

Входная проводимость — + — +-------------------------- .

Л| Ry j со Ry Rj С

а) Реализация незаземленного индуктивного элемента с потерями.

В верхний линейный провод схемы рис. П2.3 между зажимами / и 2 включен двухпо­люсник, подобный изображенному на рис. 4.11, а, отличающийся от него наличием рези-

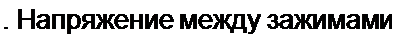стора Я₆ и комплексного сопротивления Z₂ = Я₂ + / и 2 обозначим С/₎₂, Нижний линейный провод заземлен. Из условия равенства напря­жения на входе первого ОУ нулю следует, что /₂ R + (7, +/₄)/? = 0. т. е. /₄ ~-21₂. Из условия равенства напряжения на входе ОУ нулю R 7₃ + (7₃ + /₅)я = 0, имеем 2 /₃ = -/$. Следовательно,

()₁₂ = /₂ Я + (/₂ -ь/₄)(2 Л + Z₂>4-(/₂ +

Учитывая, что /₃ = /₂ + /₄ = -7₂, а /₃ + /$ = /₂, определим U_n = -l₂ Z₂. Входной 0 U 2 ~ 2

ток 7,_х = /₂ + /₆ = —— + —12. = —2—_L Продольное сопротивление между зажима-

z₂ Z₂ Zf,

ми / и 2

012 _ -^2 -^6 _ R^ + J v>C R₂ R₆
7_ВХ Z₂-Z₆ 1 + у соС(Л₂-Л₆)

если принять Л₂ = то Z₍₂ = +у со С Л₂ /?₄. Продольная незаземленная имитирован­ная индуктивность = С /?₂ R(> имеет добротность Q = со R₂ С.

е) Реализация индуктивных и емкостных элементов второго порядка (сверхиндукгив- ных и сверхъемкостных элементов).

Под индуктивным элементом второго порядка понимают элемент,

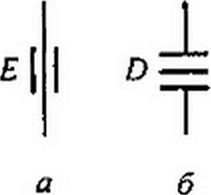
сопротивление которого при синусоидальном процессе равно (у to)² его изображение показано на

рис. П2.4, а. Емкостный элемент второго порядка имеет сопротивле­ние J-r—, его изображение показано на рис. П2.4, б (Е и D —

и _Ш)² D

действительные положительные числа). Так как (j w)²=~<o², то сопротивление индуктивного элемента второго порядка, будучи отри*.

нательным, увеличивается с ростом м, а емкостного — убывает пропорционально квад­рату частоты. Оба этих элемента для синусоидального процесса являются частотно-зави­симыми отрицательными сопротивлениями (ЧЗОС). Индуктивный элемент второго порядка

реализуется при помощи схемы на рис, 4.J1, а, если, например, Z₂=Z_A= —~. ^а Z]=Z₃=Z_S=/?, тогда Z_tx = (/ш)² R³ С². E=R³ С².

Емкостный элемент второго порядка может быть реализован р/С.Д.Н,#, если принять в ней

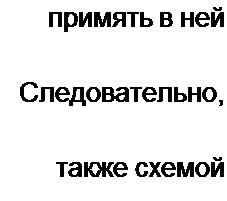Zt - Z₃ - — —-, а j we

При этом

/ ¹

^вХ (J со)² С² R

В принципе, возможна реализация индук­тивных и емкостных элементов и более высо­ких порядков, например третьего, четвертого, но использование их, как правило, затрудни­тельно из-за неустойчивости цепей с ними.

ж) Высокоомные резисторы, имитирован­ные переключаемыми конденсаторами.

В настоящее время электронные схемы часто выполняют методами интегральной технологии, создавая на одном кристалле мно­го резисторов, конденсаторов, транзисторов, диодов, ключей.

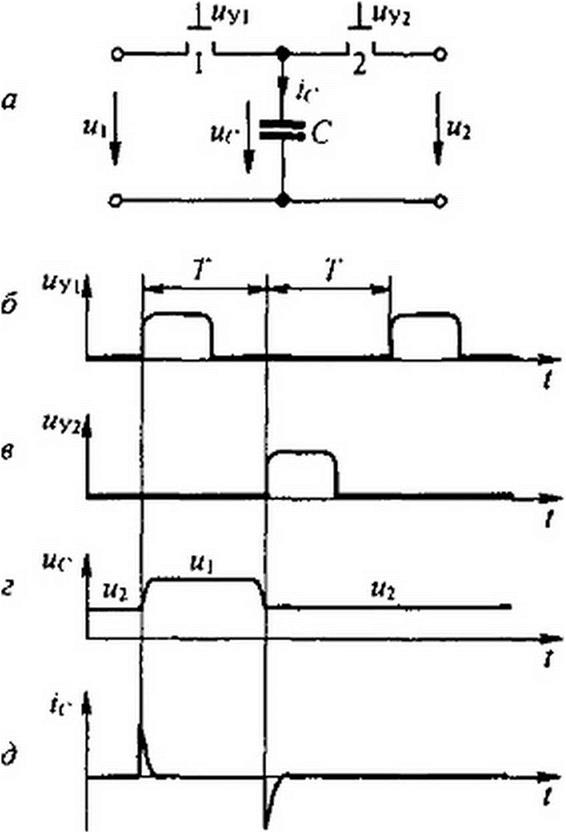
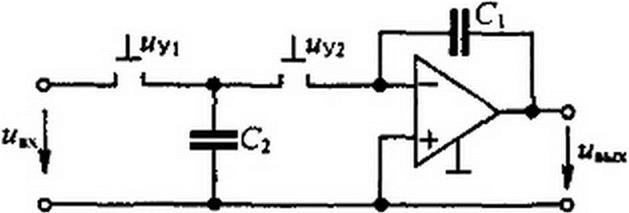
Идея имитатора R иллюстрируется на рис. П2.5, а. В схеме имеется конденсатор емкостью С и два ключа 1 и 2. открытием и закрытием которых управляют тактовыми импульсами напряжений «_У| и “_yj, посту­пающими с частотой /_z = 1/7* от кварцевого генератора. Ключ / замкнут, когда поступает импульс и_у|. При этом конденсатор заряжает­ся от и₂ до wj. Ключ 2 замкнут, когда посзу- пает импульс *_У2- Если и₂ то конденса­тор разряжается с до и₂. Через С течет ток в виде коротких импульсов (рис. П2.5, б-д).

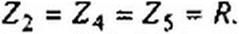
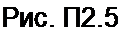
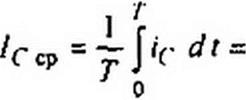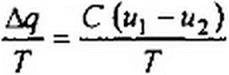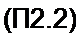Среднее значение тока i_c за время Т, поделенное на Г. равно приращению заряда конденсатора = С {u_} -и₂) \

Этот ток можно сопоставить с током, который протекал бы через резистор /?, если бы его включили между входом и выходом схемы рис. П2.5, а при замкнутых ключах / и 2

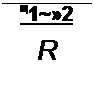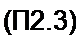Сопоставляя (П2.2) и (П2.3), устанавливаем, что имитируемое схемой рис. П2.5, а Т

резистивное сопротивление R = —. Если частоту изменений напряжений и и₂ обо­значить /. то частота тактовых импульсов f_r должна быть в несколько десятков раз больше частоты f (например, f_T = 100 /).

Положим, что в некоторой схеме цепочка из R и С, должна иметь постоянную врсме- С ни т = /?С]. Заменим/? а этой цепочке имитированным резистором, получим х-~Т.

Величиной т можно управлять, изменяя частоту Д = \/Т тактовых импульсов. Так как С| и С выполняют на одном кристалле вблизи друг от друга, то источники погреш­ности одинаковым образом влияют на С) и С, а отношение С] /С выдерживается с точностью долей процента. При этом получается значительная экономия площади крис­талла.

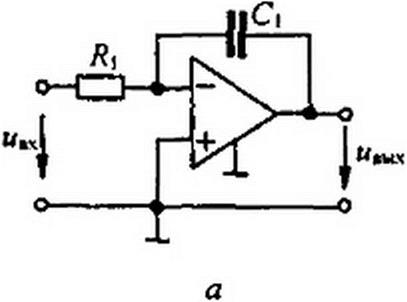
На рис. П2.6, а изображена схема интегратора на ОУ. Для нее

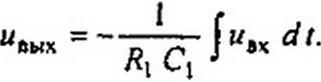Если в ней резистор R_} заменить на схемы рис. П2.5, а, получим интегратор на ком­мутируемом конденсаторе С₂ — рис. П2.6. б. Аналогичные замены применяют и в дру­гих схемах, в частности в ЯС-фильтрах.

Приложение ПЗ