Величина дерева равна произведению проводимостей ветвей этого дерева. Величина дерева рис. ГП.6, б равна ab, дерева рис. П1.6, в— Ьс, дерева рис. П1.6, г — ас. Опреде­литель графа на рис. П1.6, а

Дата: 2025-06-02; Просмотры: 13

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

& = ab + ac + bc.

‘‘В общем случае роль 1 в формуле (П1.3) может выполнять не только ток, но и напряжение.

Определитель д матрицы узловых проводимостей G (см. § 2.22), как показано в § 2.35, равен произведению трех топологических матриц (Я][^_я][Л}^г. То обстоятельство, что определитель матрицы узловых проводимостей равен сумме величин всех возможных деревьев, следует из теоремы Бине—Коши. Теорема формулируется так: определитель про­изведения двух матриц [£] [А'] (в рассматриваемом случае [£] = [/!][#/?], [Н = 1Л]^Г, при- чем матрица [£] имеет размер и матрица [Г] размер— п*т, где т S п, равен сумме произведений всех составляющих миноров максимального порядка т матриц [£] и (Г) Под соответствующими минорами понимают миноры, образованные столбцами матрицы [£} и строками матрицы (F], имеющие одинаковые номера. Матрица [л] име­ет т = у -1 строк (у — число узлов) и п = Ь — число столбцов (Ь — число обобщенных ветвей). Подматрицы порядка (у -1) матрицы [л] соответствуют деревьям графа и име­ют определитель, равный ±1. В произведении [Л][#д) элементы 4-столбна матрицы [Л] (+ 1; -1; 0) умножают на проводимость 4-ветвн (gt.-gt.O) Поэтому все ненулевые миноры порядка (у-1) матрицы [л] соответствуют деревьям схемы, а величина / ненулевого минора равна взятому со знаком плюс (минус) произведению проводимостей ветвей /-дерева. Так как перестановка строк и столбцов матрицы [А ' (по сравнению с матрицей {А]) не изменяет величины минора, то ненулевые миноры л]^г матрицы соот­ветствуют деревьям схемы и равны ±1. Так как знаки соответствующих ненулевых миноров матриц [л] [g/J и [л]^/ одинаковы, то их произведения положительны, а сумма произведений всех соответствующих миноров равна сумме величин всех возможных деревьев.

§ П1.6. Определение числа деревьев графа. Для определения числа деревьев графа положим, что проводимость каждой его ветви равна единице. Тогда величина каждого дерева также равна единице (произведение единиц равно единице). Если в рассматрива­емых условиях для исследуемой электрической цепи составить матрицу узловых прово­димостей при любом заземленном узле этой цепи, то числовое значение определителя матрицы будет равно числу возможных деревьев графа.

Пример 172. Подсчитать число деревьев для графа рис. П1.6, а, приняв а = b = с = 1:

Хотя значение числа возможных деревьев и полезно, но оно мало что дает для расче­та, так как деревья еще нужно составить и определить величину каждого дерева. Для относительно сложных схем отыскание возможных деревьев довольно трудоемко, и пото­му на практике применяют упорядоченные способы вычисления Д , один из которых рассмотрен в § П1.7.

§ П1.7. Разложение определителя по путям между двумя произвольно выбранны­ми узлами. При разложении следует выбирать узлы, относительно которых схема 8 геометрическом смысле наиболее симметрична, что упрощает подсчеты. Разложение определителя А этим метолом производят с помощью формулы

а = (П1.4)

где Р* — произведение проводимостей ветвей A-пути между выбранными узлами; Д* — определитель A-пути, подсчитанный по схеме, полученной из исходной при закорачива­нии ветвей, по которым проходит 4-путь.

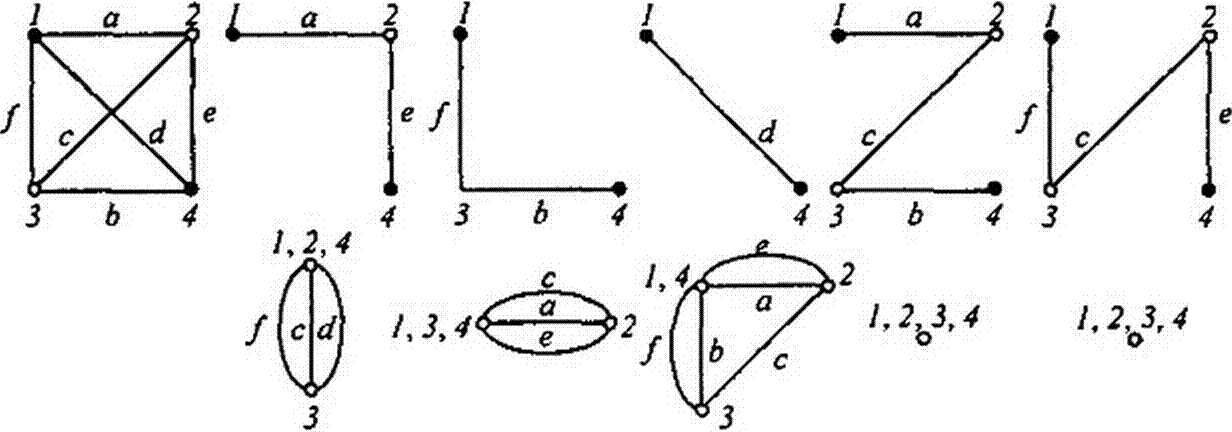
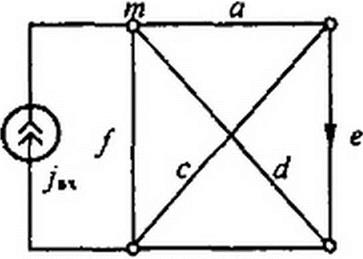
Пример 173. Найти определитель мостовой скрещенной схемы рис. П1.7. а.

Решение. Определитель Д находим путем разложения по путям между узлами / и 4 (зачерненные кружки на рис. П1.7, а). На рис. П1.7, б-е показаны пять возможных пу­тей между узлами / и 4 и соответствующие им подсхемы (подграфы) для нахождения Д*.

Для первого пути по ветвям а и е Р_} равно произведению проводимостей ветвей это­го пути: P_t = а е. При закорачивании ветвей а и е подграф представляет собой параллель­ное соединение ветвей /, с, d. Следовательно. Д) = / + с + Ь.

а б в г д е

Рис. П1.7

Для второго пути (рис. П1.7, в) по ветвям f, b Р₂ - f b, Д? = ^{а + е + с}-

Для третьего пути по ветви d (рис. П1.7, г) Д₃ = (а + е) с + \а + e){f + b) + c{J + h).

Для четвертого пути по ветвям а, с, b (рис. П 1.7, д) Р_А=асЬ\ Д< =1, так как при закорачивании этих ветвей граф вырождается в точку.

Для пятого пути по ветвям/, с, е (рис. П1.7, е) Р$= f с е\ Д₅ = 1.

Таким образом,

Д = A _t = ае(/ + с + 2>) + /6(а + е + с) +
+ d ((а + е) с + (а + е)(/ + Ь) + (/ + А) с) + а с Ь + / с е.

§ П1.8. Применение основной формулы. Как указывалось в § ГП.5, формулу (П1.3) применяют для определения входной и взаимной проводимости, передачи по току, по на­пряжению и в других целях.

Рассмотрим вопрос о том. как ею следует пользоваться. Обозначим тип узлы графа, к которым присоединяют ветвь, содержащую источник питания схемы. В дальнейшем полагаем, что источником питания является источник ЭДС либо источник тока, посколь­ку к ним можно свести любой реальный источник питания. Кроме того, считаем, что ис­точник питания только один. Если же источников питания несколько, то следует восполь­зоваться принципом наложения, последовательно находя искомую величину от действия каждого из источников, учитывая при подсчетах внутреннее сопротивление последних.

Под В_тп в (П1.3) подразумеваем напряжение источника питания, если в качестве по­следнего взят источник ЭДС или ток J_m, источника тока.

В качестве тока / в числителе левой части (П1.3) берут ток по той ветви, относитель­но которой нужно найти искомую величину. Если необходимо определить передачу от ис­точника питания к некоторой 5-ветви, то под / понимают ток этой ветви.

Число слагаемых в числителе (П1.3) равно числу возможных путей между узлами т и п, причем каждый из них должен проходить по выбранной 5-ветви (путь через источник питания нс учитывают).

В сумму ^С_ГД_Г часть слагаемых .может входить со знаком плюс, часть — со знаком минус, так как С_г может иметь знак плюс или минус. Для того чтобы определить, какой знак будет иметь С_г. руководствуются следующим: произвольно выбирают положитель­ное направление вдоль 5-ветви (ставят стрелку на 5-ветви). Если при движении по пути С, пройдем по s-ветви согласно с положительным направлением этой ветви (по стрелке на ветви), то С_г берется со знаком плюс, в противном случае — со знаком минус.

Вычисляя определитель системы А, следует учитывать внутреннее сопротивление источника литания схемы. При питании схемы от источника ЭДС д подсчитывают при закороченных узлах тп (внутреннее сопротивление источника ЭДС равно нулю). При пи­тании схемы от идеального источника тока ветвь тп, в которой включен источник, при подсчете А разрывают.

Рис. П1.8

Пример 174- Определить взаимную проводимость ветви с источником ЭДС (подклю­ченной к узлам тп) и ветви с проводимостью е рис. П1.8, а.

Решение. Для учета знака С_г примем за положительное направление ветви е на­правление, указанное стрелкой на рис. П1.8, а.

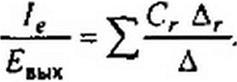Тогда

(П1.6)

В графе есть два пути между узлами т и п, которые проходят через е. Первый путь изображен на рис. П1.8, б: С₍ - а е Ь.

Этот путь берут со знаком плюс, так как при прохождении по ветви е движемся согласно с направлением стрелки на этой ветви. Поскольку при закорачивании ветвей а, е, b (ветвей этого пути) граф вырождается в точку, Д₍ = I.

Второй путь С₂ проходит по ветвям d, е, с (рис. П1.8, в). На этом пути прошли встреч­но стрелке на ветви е (рис. П1.8, б, в), поэтому С₂ = ~d е с. При закорачивании ветвей d, е, с граф вырождается в точку, следовательно, Д₂ = 1.

Для нахождения определителя системы Д закорачиваем узлы т и п (схема пита­ется от источника ЭДС) и получаем граф рис. П1.8, г. От последнего переходим к графу рис. П1.8, д.

Для вычисления Д графа рис. П1.8. д воспользуемся разложением его по путям между зачерненными точками. Между этими точками два пути: первый — по ветви е, второй — по ветвям {а + с), (б + rf). Поэтому Д = е(о + с + b + d) + (<я + с) (b + d). Таким образом.

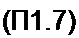/_вх _С|Д|+С₂Д₂_ aeb-dec

£_gx Д e(a + c + b + d)+(a + c)(b + d)

Для расчета передачи схемы рис. П1.8, а по напряжению между входной ветвью (вет­вью с источником ЭДС между узлами т и п) и выходной (е) воспользуемся тем, что вы­ходное напряжение на зажимах ветви у равно току /_вых этой ветви, поделенному на ее проводимость.

Следовательно.

^вых

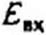Пример 175. Определить изменения, которые произой­дут в вычислениях, если схема рис. П1.8, а будет питаться не от источника ЭДС, а от источника тока рис. П1.9. Рассчи­тать передачу по току к ветви е и отношение напряжения на выходе (на ветви е) к входному току. Выходной ветвью явля­ется ветвь е. по которой проходит ток /_вых. Положительное направление для прохождения по этой ветви то же, что и в примере 174.

Решение. В отличие от примера 174 входной величи­ной является входной ток

Поэтому

/_Вых_____________________________ aeb~dec_________

j_tx (a + d + f)(c e + c b + b e) + a d (b + c) + a f (b + e)+d f (c + e) + ad f

Числитель правой части (П1.8) такой же, как и числитель правой части (П1.7). Опре­делитель Д в (П1.8) отличается от определителя в (П1.7) тем, что для (П1.7} он подсчи­тывался при питании схемы от источника ЭДС, тогда как в рассматриваемом случае он должен быть найден при литании схемы от источника тока. В этих условиях ветвь с ис­точником тока следует считать разомкнутой. Определитель для этого случая был подсчи­тан ранее (см. формулу (П1.5) в § П1.7).

Отношение выходного напряжения на ветви е к входному току

^ВЫХ _ ^8ЫХ ^а

7вх 7»х Д

Для определения входной проводимости схемы, питающейся от источника ЭДС, в числителе (П1.8) должны быть учтены все возможные пути между узлами т и п (путь через источник ЭДС исключается). Например, при вычислении входной проводимости схе­мы (рис. П1.10, а) в числителе (П1.8) должно быть взято четыре слагаемых, так хак воз­можны четыре пути между узлами тип (рис. П1.10. б-д):

/_ЯЬ1Х _ _ ab(d + c+e)+d е (a+ c + d) + dcb-l+ace'l

у_ях Д (a + b)(d +e) + (a + b)c + (d + е)с

Все С_г в числителе взяты со знаком плюс, потому что на этих путях двигались в соот­ветствии с направлением входного тока. Определитель Д (схема питается от источника ЭДС) подсчитан в соответствии с рис. ШЛО, е.

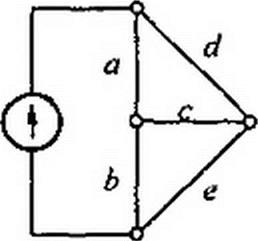
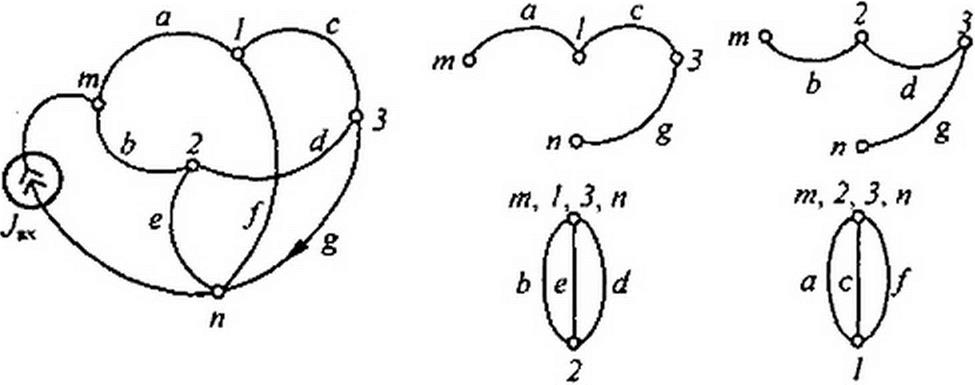
Пример 176. Определить передачу по току в двойном Т-мосте (рис. П1. II, а). Схема питается от источника тока J_8X. Выходной ветвью является ветвь g. По ней протекает ток /_вых> положительное направление которого показано стрелкой.

Решение. На рис. П1.11, б-в показаны два пути — С, и С₂ с передачами Cj = а с g и С} = bd g и соответствующие им подграфы для нахождения определителей: &i~b + e + d'_t Д₂=л + с + /.

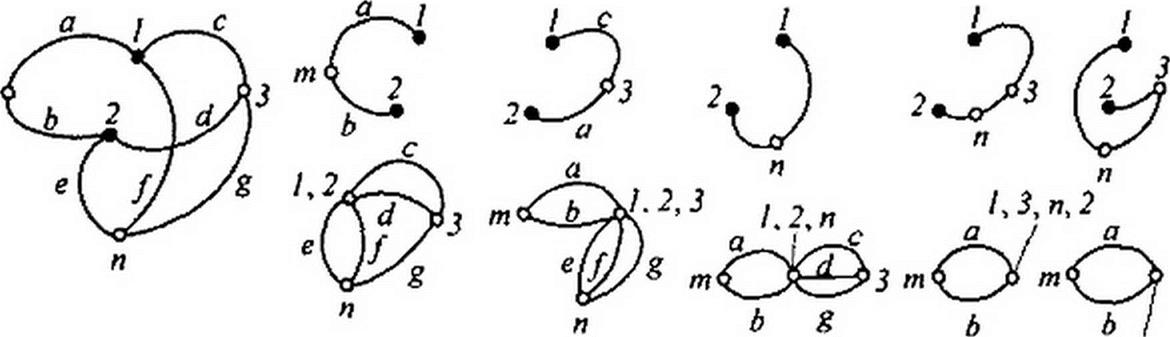
Определитель графа на рис. П1.12, а найдем методом разложения по ветвям между узлами / и 2 (зачернены). Между этими узлами имеется пять путей в соответствии с рис. П1.12, б-е. Подграфы этих путей изображены на тех же рисунках. Таким образом.

Iвых _ G Д| +С₂ Д₂ _

Д

________________________ а с g (b + е + d)+ b d g (а + с + f)___________________ ab((e + f)g + (e + /)(c + c/) + (c + rf)g) + e f{a + b)(c + d + g) + ce g(a + b) + f d g(a + b)

а б в г б е

Рис. П1.12