Передача прямого пути равна произведению передач ветзей этого пути.

Дата: 2025-06-02; Просмотры: 20
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

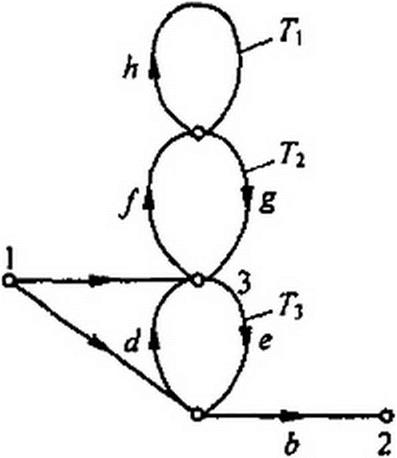
Между истоком и стоком графа может быть несколько прямых путей. Например, для схемы рис. П1.5 между истоком (узел /) и стоком (узел 2) есть два прямых пути. Первый
прямой путь — путь по ветвям с передачами а и Ь. Пере­дача этого пути Р| = а Ь.

Второй прямой путь — путь по ветвям с передачами с, е, Ь, его передача Р2 - ceb.

Ни один из других возможных путей от узла / к узлу 2 в этом графе не относится к категории прямых. Например, путь через ветви с,/, g, е, Ь не является прямым, так как на этом пути узел 3 встречается дважды. В обшей форму­ле необходимо учитывать также передачи петель обратной связи.

Петля обратной связи представляет собой замкнутый путь, вдоль которого (по кругу) каждый узел может встре­титься только один раз.

Передачу петли обратной связи часто обозначают бук­вой Т с индексом. Передача путли обратной связи равна произведению передач ветвей, образующих эту петлю.

Рис. П1.5

В графе рис. П1.5 три петли обратной связи: первая —

с Ty-h, вторая — с Т2 = / g, третья — с -е d.

Общая формула для определения передачи графа G записывается следующим обра­

 


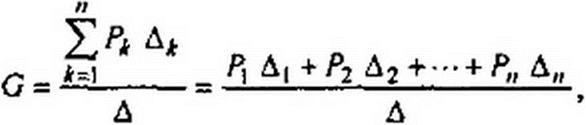зом’':

 

где — передача к-го прямого пути от истока к стоку; п — число прямых путей.

Определитель Д4 равен единице минус сумма взятых поодиночке передач петель об­ратных связей, не касающихся А--го прямого пути (эти петли могут касаться друг друга), плюс сумма попарных произведений передач петель обратных связей, не касающихся друг друга и £-го прямого пути, минус сумма тройного произведения петель обратных связей, не касающихся друг друга и к-го прямого пути, плюс и т. д.

Определитель д равен единице минус сумма взятых поодиночке передач петель об­ратных связей, касающихся и не касающихся друг друга, плюс сумма попарных произве­дений передач петель обратных связей, не касающихся друг друга, минус сумма тройного произведения петель обратных связей, не касающихся друг друга, плюс и т. д.

Пример 171, Применить формулу (П1.1) к графу рис. П1.5.

Решение. Для первого прямого пути с передачей Р ~ab определитель равен еди­нице минус сумма передач петель обратной связи, взятых поодиночке и не касающихся этого прямого пути 7] + Г2, плюс попарное произведение передач петель обратной связи, не касающихся друг друга и выбранного прямого пути.

В графе рис. П1.5 отсутствуют петли, которые бы не касались друг друга и первого прямого пути. Поэтому слагаемые с попарным произведением передач петель обратной связи, как и взятые по трое (и более), в выражении для Д) отсутствуют. Следовательно,

Д1 + Г2); T2=fg.

Для второго прямого пути

Р2 - се Ь, Д2 = 1 - 7j.

Знаменатель Д = 1 - (Г) + Т2 + Г2)+ Tj Т} = е d. В выражение для Д вошло произ­ведение Тх и Т3 двух несоприкасаюшихся петель графа. Таким образом,

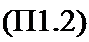с _ дб(1-Т|-Г2)+се^(1-7’|)

’'Вывод формулы см. Бессонов Л.А. ТОЭ. — М.: Высш, шк., 1978.

II. Ненаправленные графы

§ П1.5. Определение и основная формула. Ненаправленный граф представляет со­бой топологическое изображение самой электрической схемы. Узлы и ветви этого графа соответствуют ее узлам и ветвям. В ненаправленных графах, в отличие от направленных, стрелок на вегвях не ставят. Свойства ветвей характеризуют их проводимости. Передачи ветвей, имеющие размерность проводимости, в дальнейшем обозначены латинскими бук­вами а, Ь, с,.... Поскольку каждой планарной электрической цепи может быть сопостав­лена некоторая дуальная ей цепь, то каждому ненаправленному графу может соответство­

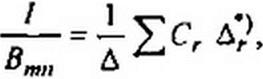вать дуальный граф. При работе с ненаправленными графами основной является формула

(П1.3)

где 1 — ток, протекающий по некоторой выбранной ветви графа, относительно которой и определяется входная или взаимная проводимость; Вт„ — напряжение (ток) источника питания схемы, присоединенного к узлам т и п; Сг — произведение проводимостей вет­вей пути между узлами тип, проходящего по выбранной ветви; ДЛ — определитель для системы, полученной из исходной при коротком замыкании (закорачивании) ветвей вы­бранного пути С,; Л — определитель исходной электрической схемы.

Правая часть (П1.3) по структуре полностью аналогична направленных графов.

Формулу (ПI 3) используют для нахождения входного сопротивления (входной про­водимости), взаимной проводимости ветвей и др.

Число членов Сг Д, в числителе (П1.3) равно числу возможных путей между узлами тип графа. В это число не входит пугь от т к п через источник питания схемы. Опреде­литель △ мог бы быть получен как определитель матрицы узловых проводимостей, составленной по методу узловых потенциалов. Однако такой способ подсчета Д доволь­но громоздок и трудоемок. Дело в том, что при вычислении Д путем раскрытия опреде­лителя упомянутой матрицы пришлось бы иметь дело с большим числом слагаемых, часть которых имела бы одинаковые абсолютные значения, но различные знаки (эти слагаемые соответствуют так называемым избыткам в каждой строке определителя).

Расчет Д, при котором нс возникает взаимно уничтожающих друг друга слагаемых,

осуществляют пугем вычисления его как суммы величин всех возможных деревьев дан­ного графа. Как упоминалось в § 2.8, под деревом понимают совокупность ветвей, кото­рые касаются всех узлов, но не образуют ни одного замкнутого контура. Ветви графа, не вошедшие в данное дерево, называют хордами или ветвями связи. Для простейшего гра-

 


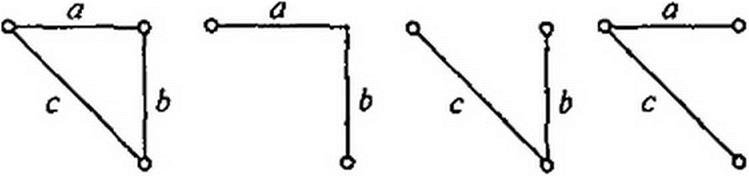а б в г

Рис. ГП .6

фа рис. ГП.6, а образуемые деревья показаны на рис. П1.6, б-г.