Сборники задач по теоретическим основам электротехники

Дата: 2025-06-02; Просмотры: 17

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

39. Сборник задач по теоретическим основам электротехники / Л.А. Бессонов, И.Г. Демидова, М.Е. Заруби, С.Э. Расовская, С.А. Миленина, В.П. Каменская. — М.: Высш, шк., 2003.

40. Задачник по теоретическим основам электротехники. Теория цепей / Под ред. К.М. Поливанова. — М.: Энергия, 1973.

4. . Сборник задач и упражнений по теоретическим основам электротехники / Под ред. П.А. Ионкияа. — М.; Энергоиздат, 1982.

42. Коровкин И.В., Чечурин В.Л., Селина Е.Б. Сборник задач по теоретическим осно­вам электротехники / Под ред. К.С. Демирчяна.

43. Теоретические основы электротехники: методические указания и контрольные за­дания / Л.А. Бессонов, И.Г. Демидова, М.Е. Заруди, В.П. Каменская, С.Э. Расовская, ТА. Любарская. — М.: Высш, шк., 2001.

Руководства по применению ЭВМ к расчету электрических цепей (алгоритмы и вычислительные методы, схемотехническое моделирование и виртуальные лаборатории)

44. Карлащук В.И. Электронная лаборатория на IBM PC. Программа WorkBench и ее применение. — М.: СОЛОН Р, 1999.

45. Электротехника и электроника в экспериментах и упражнениях: практикум на Electronics WorkBench. — Т. 1. — М.: Додэка, >999.

46. Электротехника и ТОЭ в примерах и задачах / В. А. Прянишников и др. — СПб.: Корона принт, 2001.

47. Разевиг В.Д. Система схемотехнического моделирования MicroCap V. — М.: СОЛОН, 1997.

48. Миронов В.Г., Кузовкин В.А. Моделирование на ЭВМ режимов в нелинейных це­пях. — М.: Изд-во МЭИ, 1990.

49. Миронов В.Г., Кузовкин В.А., Казанцев Ю.А. Машинный расчет характеристик аналоговых й дискретных цепей. — М.: Изд-во МЭИ, 1990.

50. Голубков В.С., Третьякова Ю.И., Цыганов В.И. Переходные процессы, нелинейные цепи и компьютерное моделирование / Под ред. В.А. Алехина. — М.: Изд-во МИРЭА, 2002.

Приложение П1

Направленные и ненаправленные графы

§ П1.1. Характеристика двух направлений в теории графов. Обобщенно граф — это совокупность узлов и соединяющих их ветвей. Каждый граф характеризуется своей топологией, т. е. информацией о том, какими ветвями и с какой проводимостью (с какой передачей и в каком направлении) связаны друг с другом узлы графа.

Теория графов — это учение об общих топографических свойствах графов и о мето­дах их расчета. Теория графов развивалась в двух направлениях: первое — матрично-то­пологическое, второе — чисто топологическое. Основные положения матрично-топологи­ческого направления были рассмотрены в гл. 2 (см. § 2.31-2.37). Основные положения чисто топологического направления рассмотрены в Приложении П1, где сначала рассмот­рены основные положения теории направленных графов (см. § П1.2-П1.5). затем нена­правленных (см. § П1.6-П1.11).

I. Направленные графы

§ П1.2. Основные определения. Направленным, или линейным, графам (графом сиг­нала, диаграммой прохождения сигнала) называют совокупность узлов и соединяющих их ветвей, стрелки на которых указывают направление передачи сигнала (воздействия) от одного узла к другому.

Узлами в направленных графах обычно являются токи и (или) потенциалы узлов ис­следуемых электрических цепей, а не узловые точки этих цепей, как это имеет место в ненаправленных графах (см. § П1.6-П1.11).

Каждая ветвь графа характеризуется своей передачей. Под передачей ветви пони­мают отношение выходной величины к входной. Так, выходная величина х₂ ветви (рис. П1.1, а) равна произведению входной величины (входного сигнала) х₍ на переда­чу а : х₂ « а.

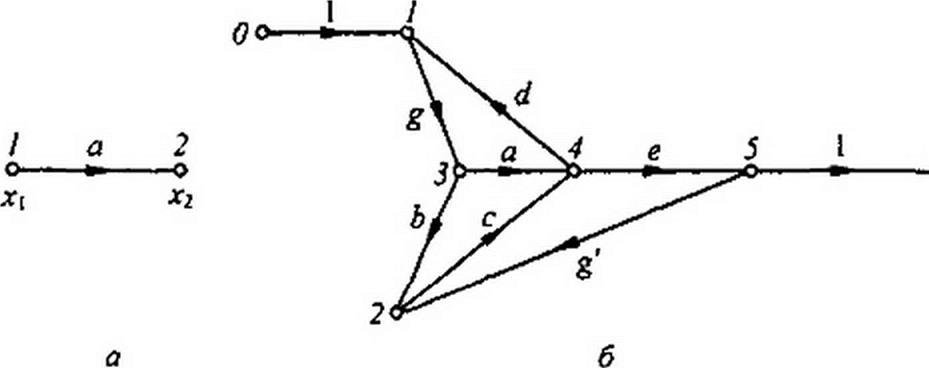
Рис. П1.!

Передача ветви может иметь размерность проводимости, сопротивления или нулевую размерность.

В том или ином узле графа, кроме входного и выходного, в общем случае может схо­диться и от него может уходить по нескольку ветвей. На рис. ГИ.1. б изображен некото­рый граф с узлами 0, 1,2, 3, 4, 5, 6. Передачи ветвей этого графа обозначены буквами а,Ь,с,.... Направление передач указано стрелками.

Под X) будем понимать узловой сигнал первого узла, под х₂ —■ узловой сигнал вто­рого узла и т. д.

Узловой сигнал Л-узла равен сумме сигналов, приходящих к этому узлу. При состав­лении узлового сигнала Л-узла выходящие из этого узла сигналы не учитываются; они учитываются при составлении узловых сигналов тех узлов, к которым эти сигналы подхо­дят. Так, узловой сигнал первого узла графа рис. П1.1, б, х₍ =1 x$+d х₄. второго узла — х₂ = Ь х₃ + g’ х₅, третьего узла — х₃ = g Х) и т. д.

Узел графа, выражающий собой величину, принятую в изучаемой системе за входную, обычно изображают на чертеже слева, а узел, соответствующий выходной величине, — справа.

Принято изображать граф так, чтобы от входного узла отходила только одна ветвь, а подходящих ко входному узлу ветвей вообще не было.

Аналогично, к выходному узлу должна подходить только одна ветвь (отходящих от него ветвей не должно быть). Это можно сделать, ведя в граф дополнительные узлы и ветви, передачи которых равны единице. В графе на рис. П1.1, б дополнительными узлами яв­ляются узлы 1 и 5. Между входным узлом 0 и дополнительным узлом / имеется ветвь с передачей /. На рис. ГП. 1, б дополнительный узел 5 соединен с выходным узлом 6 вет­вью с передачей, равной единице. Часто узлы, передача между которыми равна единице, обозначают одинаково; например, для схемы на рис. П1.1, б узел 0 можно назвать узлом 1 (тогда на рисунке будет два узла, обозначенных цифрой /).

§ П1 «3. Переход от изучаемой системы к направленному графу. Для того чтобы от какой-либо электрической цепи перейти к соответствующему ей направленному графу, применяют различные методы в зависимости от того, каким образом записывают уравне­ния для этих цепей: на основании законов Кирхгофа, используя метод узловых потенциа­лов или метод контурных токов и т. д.

Направленный граф содержит ту же информацию, что и система уравнений. Только информация эта выражена графически.

Если за основу взять уравнения, составленные на основании законов Кирхгофа, то узлами графа являются токи ветвей и напряжения на элементах схемы. В том случае, ког­да за основу взяты уравнения, составленные методом узловых потенциалов, узлы графа будут выражать собой потенциалы узловых точек схемы, узловые и искомые токи (напря­жения).

При некотором навыке граф вычерчивают, даже не записывая самих уравнений, послуживших основой для его составления.

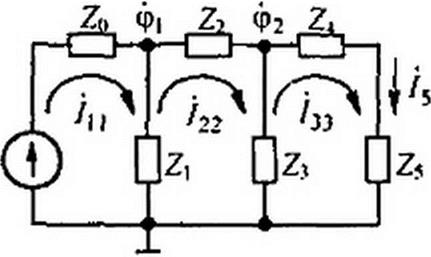
Упорядоченный переход от заданной электрической схемы к направленному графу, минуя этап составления уравнений, рассмотрим, положив в основу метод контурных токов (переход от рис. П1.2 к рис. П1.3, а).

Рис. П1.3

Направления контурных токов во всех контурах выбираем одинаковыми, например по часовой стрелке. Число узлов в графе равно числу контурных токов плюс число, не рав­ных нулю контурных ЭДС, плюс выходная величина.

Каждому контурному току, каждой контурной ЭДС и выходной величине соответству­ет свой узел. Так, схеме рис. П 1.2, в которой три контурных тока— Ль^зз-бз, одна кон­турная ЭДС и выходная величина — ток /₅, соответствует граф рис. П1.3, а, в котором имеется пять узлов.

Узлы /_кк располагаем в серединах соответствующих контуров, а узлы Е_кк и узел выходной величины выносим на периферию рисунка. Соединим нарисованные узлы вет­вями, указываем на них стрелки и записываем значения передач ветвей. Каждый узел соединен с узлом £** ветвью с передачей b_kk - l/Z_kk , где Z_kk— собственное сопротив­ление Ar-контура. Стрелка на этой ветви направлена к узлу i_kk. Числовое значение — может быть и положительным и отрицательным. Оно положительно, если суммарная ЭДС контура, подсчитанная согласно направлению контурного тока положительна. Кроме того, каждый узел /_кк соединен с каким-то другим узлом / (если между контурами * и р на схеме есть общая ветвь) двумя ветвями. Одна ветвь имеет стрелку, направленную к узлу /_кк, и передачу = Z^(Z_kki где Z_kp— сопротивление смежной ветви между к- и р-контурами. На другой ветви стрелка направлена к узлу i _рр. Ее передача

“ ZkplZpp’ где ?РР— собственное сопротивление р-контура.

При согласном направлении всех контурных токов передачи всех ветвей между узла­ми к и р положительны.

По методу узловых потенциалов граф строят так же, как и по методу контурных то­ков, только узлами графов являются потенциалы узлов схемы, узловые токи и выходная величина.

Если в электрической схеме узлы к и р соединены ветвью с проводимостью Y_kp, а суммарная проводимость ветвей, сходящихся в узлах к и р, обозначена соответственно через y_w и то на графе между узлами к и р имеется две ветви (рис. П1.3, 6). На одной из них стрелка направлена к узлу ф*, а ее передача a_kp = Y^ /У_кк . На другой стрел­ка направлена к узлу ф*. а ее передача а_рк = Y_kpfY_kk. Так, на рис. П1.3, б при к = 1, р = 2 а₁₂ - У₎₂ / У_м. а₂| = У₂| / К,₂. Первый индекс у а указывает узел, к которому на­правлена стрелка, второй — узел, от которого направлена стрелка. Если узлы к »р на схе­ме не соединены ветвью с проводимостью У_Л/>, то и на графе узлы ф* и Ф_р не соедине­ны ветвями. Узел ф_А соединен с узлом узлового тока J_kk ветвью с передачей а_кк - >

направленной к узлу ф*. Искомому току 1_к), в ветви с проводимостью Y^ (полагаем его направленным от узла к к узлу р) на графе соответствует узел выходной величины

В соответствии с законом Ома для участка цепи к узлу графа !_кр должны подходить две ветви, стрелки на которых направлены к узлу !_кр. Передача от узла ф_А равна Y^, передача от узла ф_р равна -У^. Если какой-либо из этих узлов заземлен, то этот узел и передача от него будут отсутствовать.

Если граф составляют для цепи постоянного тока, то комплексное сопротивление Z следует заменить на резистор сопротивлением R, комплексную проводимость У— на ак­тивную проводимость G, а точки над свидетельствующие о синусоидальном характере изменения этих величин во времени, не ставят.

Пример 169. Составить граф для лестничной схемы рис. П1.2, считая входной вели­чиной ЭДС £|, а выходной ток /₅.

Решение. Граф на рис. П1.3. а составлен по методу контурных токов для уравне­ний, записанных в комплексной форме:

/_н (Z_o + Z])-/₂₂ Z₍ - £₍ или /_н = />_н £₍ + Ь₁₂ /₂₂;

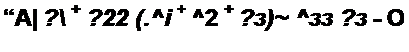или /₂₂ - 6₂₍ /|, + 6₂₃ /₃₃;

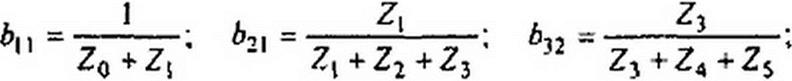
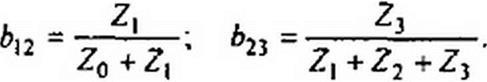где

Передача от узла /₃₃ к узлу /$ равна единице, так как /₅ -1- /₃₃.

Пример 170. Составить граф для схемы рис. Ш.2 методом узловых потенциалов.

Решение. Обозначим X₀=l/Z₀; ^=1/2,; F₂=l/Z₂; У45 — 1/(Z₄);

Ун » Xq +• У₍ + У₂Узз = У2 + Уз + У4- Запишем систему уравнений;

Ф| Уц + ф₂ (-Уг)--*6i ^или Ф1 = ^Ли Л1 ^+ai2 Фг»
Ф1 (-^)⁺Ф2 *22 ^{= 0 или} Фз “*21 Фь

4 = ф₂ У_4!.

На рис. П1.3, 6 йГ| j = 1/У_н ; а₎₂ = У₂/Уц ; а₂₁ = У2/У22 • Предполагается, что ни один из знаменателей выражений b^b^, для значений параметров схемы, находящихся в рабочем диапазоне, не равен нулю.

Порядок расположения узлов на чертеже может быть любым (расположение узлов входа и выхода уже рассматривалось), однако рекомендуется это делать таким образом, чтобы последовательность при движении слева направо в наибольшей степени соответствовала фактическому прохождению сигнала (информации) от входа к выходу.

В зависимости от того, какие величины выбраны в качестве узлов, для одной и той же схемы граф имеет различную структуру и различную сложность. Заметим, что если в схеме имеется несколько источников сигнала (несколько источников тока или ЭДС), то пользуются принципом наложения, т. е. сначала определяют выходную величину для графа, в котором сигнал действует от первого источника, затем выходную величину для графа, в котором сигнал действует от второго источника, и т. д. После этого суммируют выражения для выходной величины. Однако можно поступить и иначе, а именно граф с несколькими источниками сигналов одинаковой частоты свести к графу с одним источни­ком (рис. ГП.4). С этой целью один из сигналов, например сигнал Е на рис. П1.4, а, при­мем за базисный. Узлы остальных сигналов (в примере узел тока j) объединяют с базис­ным, так изменяя передачи от этих узлов к остальным, чтобы сигналы, подходящие к ним, остались неизменными.

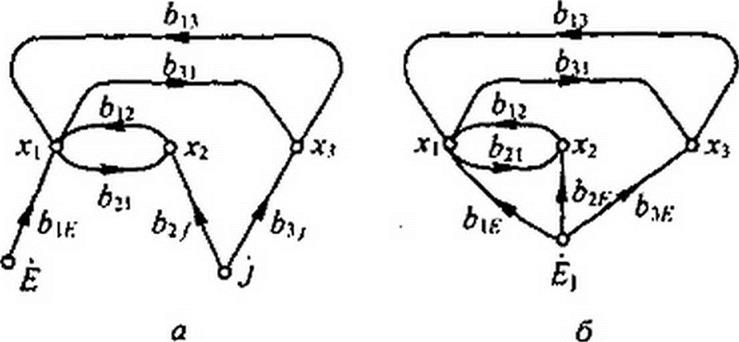
Рис. П1.4

В рассматриваемом примере объединяем узел j с узлом Ё (рис. П 1.4, б) и изменя­ем передачи Ь_1} и на 6_2/,- и Ь_зк исходя из условий b_ZK Е - q_ZJ byf. E-q^jJ. Отсюда Л_2Л- £ = b_ZJ j\ b_3/.; Е - b_3/ J. Когда граф составлен, его используют для опреде­ления передачи от истока к стоку. Входной сигнал называют истоком, выходной — стокам.

§ П1.4. Общая формула для передачи направленного (сигнального) графа. В 1956 г. Мэзон предложил общую формулу для определения передачи графа. Эта форму­ла является основной при расчете графов. Прежде чем перейти к ней, познакомимся с не­которыми новыми понятиями.

Прямой путь Р — это путь вдоль стрелок от истока к стоку, при прохождении которо­го ни один из узлов не встречается более одного раза.